


2022-2023学年江苏省仪征市七下数学期末联考模拟试题含答案
展开2022-2023学年江苏省仪征市七下数学期末联考模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项
1.考生要认真填写考场号和座位序号。
2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。
3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。
一、选择题(每小题3分,共30分)
1.在![]() 中,斜边
中,斜边![]() ,则
,则![]()
![]()
A.10 B.20 C.50 D.100
2.若分式![]() 的值为0,则x的值为( )
的值为0,则x的值为( )
A.-2 B.0 C.2 D.±2
3.用配方法解关于![]() 的一元二次方程
的一元二次方程![]() ,配方后的方程可以是( )
,配方后的方程可以是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
4.如图,一个运算程序,若需要经过两次运算才能输出结果,则![]() 的取值范围为
的取值范围为![]()
![]()

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.以下列长度的线段为边,能构成直角三角形的是( )
A.2,3,4 B.4,5,6 C.8,13,5 D.1,![]() ,1
,1
6.在反比例函数y=![]() 的图象的每一条曲线上,y都随x的增大而减小,则m的值可以是( )
的图象的每一条曲线上,y都随x的增大而减小,则m的值可以是( )
A.0 B.1 C.2 D.3
7.如图,点P是双曲线y=![]() (x>0)上的一个动点,过点P作PA⊥x轴于点A,当点P从左向右移动时,△OPA的面积( )
(x>0)上的一个动点,过点P作PA⊥x轴于点A,当点P从左向右移动时,△OPA的面积( )
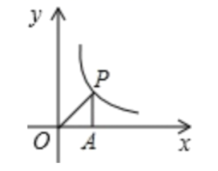
A.逐渐变大 B.逐渐变小 C.先增大后减小 D.保持不变
8.矩形的对角线长为20,两邻边之比为3 : 4,则矩形的面积为( )
A.20 B.56 C.192 D.以上答案都不对
9.下列多项式中,分解因式不正确的是( )
A.a2+2ab=a(a+2b) B.a2-b2=(a+b)(a-b)
C.a2+b2=(a+b)2 D.4a2+4ab+b2=(2a+b)2
10.对于任意的正数m,n定义运算※为:m※n=![]() 计算(3※2)×(8※12)的结果为( )
计算(3※2)×(8※12)的结果为( )
A.2-4![]() B.2 C.2
B.2 C.2![]() D.20
D.20
二、填空题(本大题共有6小题,每小题3分,共18分)
11.二次函数![]() 的函数值
的函数值![]() 自变量
自变量![]() 之间的部分对应值如下表:
之间的部分对应值如下表:
| … |
| 0 | 1 | 4 | … |
| … | 4 |
|
|
| … |
此函数图象的对称轴为_____
12.已知反比例函数![]() 的图象在第二、四象限,则
的图象在第二、四象限,则![]() 取值范围是__________
取值范围是__________
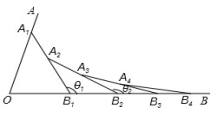
13.如图 , 在 射 线 OA、OB 上 分 别 截 取 OA1、OB1, 使 OA1 OB1;连接 A1B1 , 在B1 A1、B1B 上分别截取 B1 A2、B1B2 ,使 B1 A2B1B2 ,连接 A2 B2;……依此类推,若A1B1O,则 A2018 B2018O =______________________.
14.若解分式方程![]() 的解为负数,则
的解为负数,则![]() 的取值范围是____
的取值范围是____
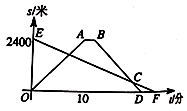
15.小明租用共享单车从家出发,匀速骑行到相距![]() 米的图书馆还书.小明出发的同时,他的爸爸以每分钟
米的图书馆还书.小明出发的同时,他的爸爸以每分钟![]() 米的速度从图书馆沿同一条道路步行回家,小明在图书馆停留了
米的速度从图书馆沿同一条道路步行回家,小明在图书馆停留了![]() 分钟后沿原路按原速返回.设他们出发后经过
分钟后沿原路按原速返回.设他们出发后经过![]() (分)时,小明与家之间的距离为
(分)时,小明与家之间的距离为![]() (米),小明爸爸与家之间的距离为
(米),小明爸爸与家之间的距离为![]() (米),图中折线
(米),图中折线![]() 、线段
、线段![]() 分别表示
分别表示![]() 、
、![]() 与
与![]() 之间的函数关系的图象.小明从家出发,经过___分钟在返回途中追上爸爸.
之间的函数关系的图象.小明从家出发,经过___分钟在返回途中追上爸爸.
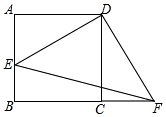
16.如图,在正方形ABCD中,E为AB中点,连结DE,过点D作DF⊥DE交BC的延长线于点F,连结EF,若AE=1,则EF的值为__.
三、解下列各题(本大题共8小题,共72分)
17.(8分)某市米厂接到加工大米任务,要求![]() 天内加工完
天内加工完![]() 大米.米厂安排甲、乙两车间共同完成加工任务,乙车间加工中途停工一段时间维修设备,然后改变加工效率继续加工,直到与甲车间同时完成加工任务为止,设甲、乙两车间各自加工大米数量
大米.米厂安排甲、乙两车间共同完成加工任务,乙车间加工中途停工一段时间维修设备,然后改变加工效率继续加工,直到与甲车间同时完成加工任务为止,设甲、乙两车间各自加工大米数量![]() 与甲车间加工时间
与甲车间加工时间![]() (天)之间的关系如图1所示;未加工大米
(天)之间的关系如图1所示;未加工大米![]() 与甲车间加工时间
与甲车间加工时间![]() (天)之间的关系如图2所示,请结合图像回答下列问题
(天)之间的关系如图2所示,请结合图像回答下列问题

(1)甲车间每天加工大米__________;![]() =______________;
=______________;
(2)直接写出乙车间维修设备后,乙车间加工大米数量![]() 与
与![]() (天)之间的函数关系式,并指出自变量的取值范围.
(天)之间的函数关系式,并指出自变量的取值范围.
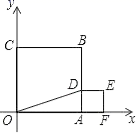
18.(8分)如图,在平面直角坐标系中,点D是正方形OABC的边AB上的动点,OC=1.以AD为一边在AB的右侧作正方形ADEF,连结BF交DE于P点.
(1)请直接写出点A、B的坐标;
(2)在点D的运动过程中,OD与BF是否存在特殊的位置关系?若存在,试写出OD与BF的位置关系,并证明;若不存在,请说明理由.
(3)当P点为线段DE的三等分点时,试求出AF的长度.
19.(8分)顶点都在格点上的多边形叫做格点多边形.以下![]() 的网格中,小正方形的边长为1.请按以下要求,画出一个格点多边形(要标注其它两个顶点字母).
的网格中,小正方形的边长为1.请按以下要求,画出一个格点多边形(要标注其它两个顶点字母).
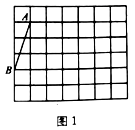
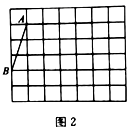
(1)在图甲中,画一个以![]() 为一边且面积为15的格点平行四边形;
为一边且面积为15的格点平行四边形;
(2)在图乙中,画一个以![]() 为一边的格点矩形.
为一边的格点矩形.
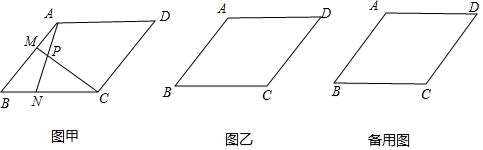
20.(8分)在▱ABCD中,AB=BC=9,∠BCD=120°.点M从点A出发沿射线AB方向移动.同时点N从点B出发,以相同的速度沿射线BC方向移动,连接AN,CM,直线AN、CM相交于点P.
(1)如图甲,当点M、N分别在边AB、BC上时,
①求证:AN=CM;
②连接MN,当△BMN是直角三角形时,求AM的值.
(2)当M、N分别在边AB、BC的延长线上时,在图乙中画出点P,并直接写出∠CPN的度数.
21.(8分)已知关于x的一元二次方程x2﹣(n+3)x+3n=1.求证:此方程总有两个实数根.
22.(10分)如图,已知点A.B在双曲线y=![]() (x>0)上,AC⊥x轴于C,BD⊥y轴于点D,AC与BD交于点P,P是AC的中点.
(x>0)上,AC⊥x轴于C,BD⊥y轴于点D,AC与BD交于点P,P是AC的中点.
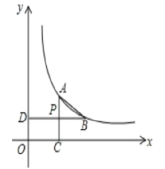
(1)设A的横坐标为m,试用m、k表示B的坐标.
(2)试判断四边形ABCD的形状,并说明理由.
(3)若△ABP的面积为3,求该双曲线的解析式.
23.(10分)数257-512能被120整除吗?请说明理由.
24.(12分)在一次数学实践活动中,观测小组对某品牌节能饮水机进行了观察和记录,当观察到第![]() 分钟时,水温为
分钟时,水温为![]() ,记录的相关数据如下表所示:
,记录的相关数据如下表所示:
| 第一次加热、降温过程 | … | ||||||||||
t(分钟) | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | … |
y( | 20 | 40 | 60 | 80 | 100 | 80 | 66.7 | 57.1 | 50 | 44.4 | 40 | … |
(饮水机功能说明:水温加热到![]() 时饮水机停止加热,水温开始下降,当降到
时饮水机停止加热,水温开始下降,当降到![]() 时饮水机又自动开始加热)
时饮水机又自动开始加热)
请根据上述信息解决下列问题:
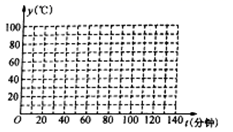
(1)根据表中数据在如图给出的坐标系中,描出相应的点;
(2)选择适当的函数,分别求出第一次加热过程和第一次降温过程![]() 关于
关于![]() 的函数关系式,并写出相应自变量的取值范围;
的函数关系式,并写出相应自变量的取值范围;
(3)已知沏茶的最佳水温是![]() ,若18:00开启饮水机(初始水温
,若18:00开启饮水机(初始水温![]() )到当晚20:10,沏茶的最佳水温时间共有多少分钟?
)到当晚20:10,沏茶的最佳水温时间共有多少分钟?
参考答案
一、选择题(每小题3分,共30分)
1、D
2、C
3、A
4、C
5、D
6、A
7、D
8、C
9、C
10、B
二、填空题(本大题共有6小题,每小题3分,共18分)
11、x=2.
12、m>5
13、![]()
14、![]()
15、1.
16、![]()
三、解下列各题(本大题共8小题,共72分)
17、解:(1)![]() ;
;![]() ; (2)
; (2)![]() ,
,![]()
18、(1)A(1,0),B(1,1);(2)OD⊥BF,理由见解析;(3)当P点为线段DE的三等分点时,AF的长度为2或2.
19、(1)见解析;(2)见解析.
20、(1)①见解析②3或6(2)120°
21、见解析.
22、(1)B(2m,![]() );(2)四边形ABCD是菱形,理由见解析;(3)y=
);(2)四边形ABCD是菱形,理由见解析;(3)y=![]() .
.
23、能,见解析.
24、(1)见解析;(2)第一次加热:![]() ,
,![]() ;第一次降温:
;第一次降温:![]() ,
,![]() ;(3)
;(3)![]() 分钟.
分钟.
江苏省仪征市第三中学2022-2023学年七下数学期末质量检测模拟试题含答案: 这是一份江苏省仪征市第三中学2022-2023学年七下数学期末质量检测模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,方程x等内容,欢迎下载使用。
江苏省仪征市古井中学2022-2023学年数学七下期末统考试题含答案: 这是一份江苏省仪征市古井中学2022-2023学年数学七下期末统考试题含答案,共7页。试卷主要包含了答题时请按要求用笔等内容,欢迎下载使用。
2022-2023学年江苏省苏州昆山、太仓市七下数学期末联考模拟试题含答案: 这是一份2022-2023学年江苏省苏州昆山、太仓市七下数学期末联考模拟试题含答案,共8页。












