


2022-2023学年广西北海市银海区七下数学期末监测模拟试题含答案
展开2022-2023学年广西北海市银海区七下数学期末监测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。
2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题(每小题3分,共30分)
1.一次函数![]() 的图像经过点
的图像经过点![]() ,且
,且![]() 的值随
的值随![]() 值的增大而增大,则点
值的增大而增大,则点![]() 的坐标可以为( )
的坐标可以为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1500m,小敏行走的路线为B→A→G→E,小聪行走的路线为B→A→D→E→F,若小敏行走的路程为3100m,则小聪行走的路程为( )m.
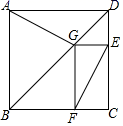
A.3100 B.4600 C.3000 D.3600
3.下列标志既是轴对称图形又是中心对称图形的是( )
A. B.
B. C.
C. D.
D.
4.明明家与学校的图书馆和食堂在同一条直线上,食堂在家和图书馆之间。一天明明先去食堂吃了早餐,接着去图书馆看了一会书,然后回家。如图反应了这个过程中明明离家的距离y与时间x之间的对应关系,下列结论:①明明从家到食堂的平均速度为0.075km/min;②食堂离图书馆0.2km;③明明看书用了30min;④明明从图书馆回家的平均速度是0.08km/min,其中正确的个数是( )
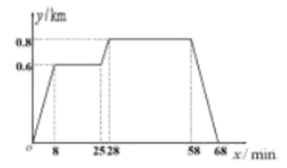
A.1个 B.2个 C.3个 D.4个
5.点![]() 向右平移
向右平移![]() 个单位后落在直线
个单位后落在直线![]() 上,则
上,则![]() 的值为( )
的值为( )
A.2 B.3 C.4 D.5
6.如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,且BD=2CD,BC=6cm,则点D到AB的距离为( )
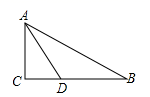
A.4cm B.3cm C.2cm D.1cm
7.矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点,将矩形右下角沿
的中点,将矩形右下角沿![]() 折叠,使点
折叠,使点![]() 落在矩形内部点
落在矩形内部点![]() 位置,如图所示,则
位置,如图所示,则![]() 的长度为( )
的长度为( )
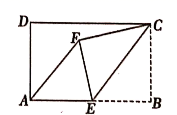
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.向最大容量为60升的热水器内注水,每分钟注水10升,注水2分钟后停止1分钟,然后继续注水,直至注满.则能反映注水量与注水时间函数关系的图象是 ( )
A.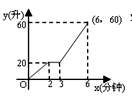 B.
B.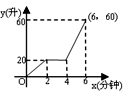
C.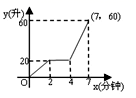 D.
D.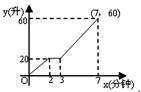
9.估计![]() 的值在( )
的值在( )
A.2和3之间 B.3和4之间
C.4和5之间 D.5和6之间
10.如图,在![]() 中,
中,![]() ,
,![]() ,分别以AC,BC为边向
,分别以AC,BC为边向![]() 外作正方形,两个正方形的面积分别记为
外作正方形,两个正方形的面积分别记为![]() ,
,![]() ,则
,则![]() 等于( )
等于( )
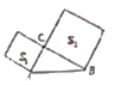
A.30 B.150 C.200 D.225
二、填空题(本大题共有6小题,每小题3分,共18分)
11.以正方形ABCD一边AB为边作等边三角形ABE,则∠CED=_____.
12.某公司招聘英语翻译,听、说、写成绩按3∶3∶2计入总成绩.某应聘者的听、说、写成绩分别为80分,90分,95分(单项成绩和总成绩满分均为百分制),则他的总成绩为____________分.
13.五边形从某一个顶点出发可以引_____条对角线.
14.直线![]() 与两坐标轴围成的三角形的面积为4,则
与两坐标轴围成的三角形的面积为4,则![]() 的值为______.
的值为______.
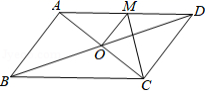
15.把直线y=﹣2x﹣1沿x轴向右平移3个单位长度,所得直线的函数解析式为_____.
16.如图,![]() ABCD的对角线相交于点O,且AD
ABCD的对角线相交于点O,且AD![]() CD,过点O作OM
CD,过点O作OM![]() AC,交AD于点M.如果
AC,交AD于点M.如果![]() CDM的周长为8,那么
CDM的周长为8,那么![]() ABCD的周长是__.
ABCD的周长是__.
三、解下列各题(本大题共8小题,共72分)
17.(8分)如图,在矩形![]() 中,点
中,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,且
上,且![]() .
.
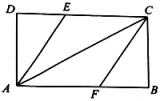
(1)求证:四边形![]() 是平行四边形.
是平行四边形.
(2)若四边形![]() 是菱形,
是菱形,![]() ,
,![]() ,求菱形
,求菱形![]() 的周长.
的周长.
18.(8分)先观察下列等式,再回答问题:
①![]() =1+1=2;
=1+1=2;
②![]() =2+
=2+ ![]() =2
=2 ![]() ;
;
③![]() =3+
=3+![]() =3
=3![]() ;…
;…
(1)根据上面三个等式提供的信息,请猜想第四个等式;
(2)请按照上面各等式规律,试写出用 n(n 为正整数)表示的等式,并用所学知识证明.
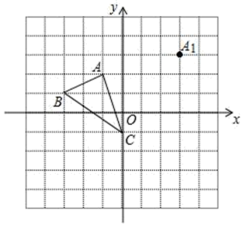
19.(8分)如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(0,﹣1).
(1)写出A、B两点的坐标
(1)经过平移,△ABC的顶点A移到了点A1,画出平移后的△A1B1C1;若△ABC内有一点P(a,b),直接写出按(1)的平移变换后得到对应点P1的坐标.
(3)画出△ABC绕点C旋转180°后得到的△A1B1C1.
20.(8分)任丘市举办一场中学生乒乓球比赛,比赛的费用y(元)包括两部分:一部分是租用比赛场地等固定不变的费用b(元),另一部分费用与参加比赛的人数(x)人成正比.当x=20时,y=1600;当x=30时,y=1.
(1)求y与x之间的函数关系式;
(2)如果承办此次比赛的组委会共筹集;经费6350元,那么这次比赛最多可邀请多少名运动员参赛?
21.(8分)如图.已知A、B两点的坐标分别为A(0,![]() ),B(2,0).直线AB与反比例函数
),B(2,0).直线AB与反比例函数![]() 的图象交于点C和点D(
的图象交于点C和点D(![]() 1,a).
1,a).
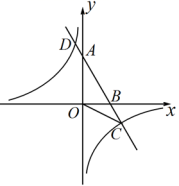
(1)求直线AB和反比例函数的解析式.
(2)求∠ACO的度数.
22.(10分)如图,矩形OABC的顶点A,C在x,y轴正半轴上,反比例函数![]() 过OB的中点D,与BC,AB交于M,N,且已知D(m,2),N(8,n).
过OB的中点D,与BC,AB交于M,N,且已知D(m,2),N(8,n).
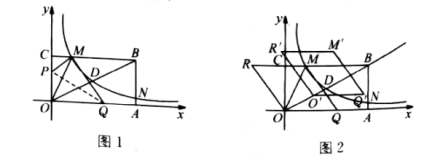
(1)求反比例函数的解析式;
(2)若将矩形一角折叠,使点O与点M重合,折痕为PQ,求点P的坐标;
(3)如图2,若将![]() 沿OM向左翻折,得到菱形OQMR,将该菱形沿射线OB以每秒
沿OM向左翻折,得到菱形OQMR,将该菱形沿射线OB以每秒![]() 个单位向上平移t秒.
个单位向上平移t秒.
① 用t的代数式表示![]() 和
和![]() 的坐标;
的坐标;
② 要使该菱形始终与反比例函数图像有交点,求t的取值范围.
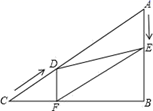
23.(10分)如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出t的值,如果不能,说明理由;
(3)在运动过程中,四边形BEDF能否为正方形?若能,求出t的值;若不能,请说明理由.
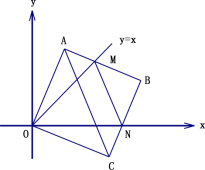
24.(12分)在平面直角坐标中,边长为 2 的正方形 OABC 的两顶点 A、C 分别在 y 轴、x 轴的正半轴上,点 O 在原点.现将正方形 OABC 绕 O 点顺时针旋转,当 A 点第一次落在直线 y=x 上时停止旋转,旋转过程中,AB 边交直线 y=x于点 M,BC 边交 x 轴于点 N(如图).
(1)求边 OA 在旋转过程中所扫过的面积;
(2)旋转过程中,当 MN 和 AC 平行时,求正方形 OABC 旋转的度数;
(3)试证明在旋转过程中, △MNO 的边 MN 上的高为定值;
(4)设△MBN 的周长为 p,在旋转过程中,p 值是否发生变化?若发生变化,说明理由;若不发生变化,请给予证明,并求出 p 的值.
参考答案
一、选择题(每小题3分,共30分)
1、A
2、B
3、C
4、D
5、A
6、C
7、A
8、D
9、C
10、D
二、填空题(本大题共有6小题,每小题3分,共18分)
11、30°或150°.
12、87.1
13、1
14、![]()
15、y=﹣2x+1
16、16
三、解下列各题(本大题共8小题,共72分)
17、(1)见解析;(2)20.
18、(1)![]()
![]()
![]() ;(2)
;(2)![]()
![]() ,证明见解析.
,证明见解析.
19、(1)A(﹣1,1),B(﹣3,1);(1)P1(a+4,b+1);(3)见解析.
20、 (1) 函数的解析式是:y=40x+800;(2) 这次比赛最多可邀请138名运动员.
21、(1)y=![]() x+
x+![]() ,y=﹣
,y=﹣![]() ;(2)∠ACO=30°;
;(2)∠ACO=30°;
22、(1)![]() ;(2)
;(2)![]() ;(3)①
;(3)①![]() ;
;![]() ;②
;② ![]()
23、(1)证明见解析;(2)当t=10时,四边形AEFD是菱形;(3)四边形BEDF不能为正方形,理由见解析.
24、(1)OA 在旋转过程中所扫过的面积为 0.5π ;(1)旋转过程中,当 MN 和 AC 平行时,正方形 OABC 旋转的度数为 25°-11.5°=11.5 度;(3)MN 边上的高为 1(2)在旋转正方形 OABC 的过程中,p 值无变化.见解析.
广西北海市银海区2023-2024学年九年级数学第一学期期末检测模拟试题含答案: 这是一份广西北海市银海区2023-2024学年九年级数学第一学期期末检测模拟试题含答案,共9页。试卷主要包含了考生要认真填写考场号和座位序号,下列事件中,是随机事件的是等内容,欢迎下载使用。
广西北海市银海区2023-2024学年九年级数学第一学期期末监测模拟试题含答案: 这是一份广西北海市银海区2023-2024学年九年级数学第一学期期末监测模拟试题含答案,共8页。试卷主要包含了图1是一个地铁站入口的双翼闸机,下列命题中,不正确的是,下列方程中,是一元二次方程的是等内容,欢迎下载使用。
2023-2024学年广西北海市银海区八年级数学第一学期期末学业质量监测模拟试题含答案: 这是一份2023-2024学年广西北海市银海区八年级数学第一学期期末学业质量监测模拟试题含答案,共6页。试卷主要包含了一组数据,计算等内容,欢迎下载使用。












