


2022-2023学年山西省运城市芮城县数学七下期末经典试题含答案
展开2022-2023学年山西省运城市芮城县数学七下期末经典试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
请考生注意:
1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。
2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。
一、选择题(每小题3分,共30分)
1.如图正方形ABCD中,点E、F分别在CD、BC边上,△AEF是等边三角形.以下结论:①EC=FC;②∠AED=75°;③AF=![]() CE;④EF的垂直平分线是直线AC.正确结论个数有( )个.
CE;④EF的垂直平分线是直线AC.正确结论个数有( )个.
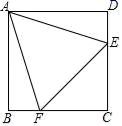
A.1 B.2 C.3 D.4
2.不等式![]() 的解集在数轴上表示为( )
的解集在数轴上表示为( )
A.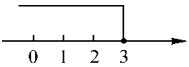 B.
B.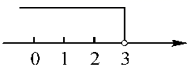 C.
C.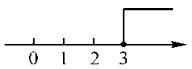 D.
D.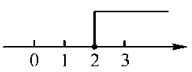
3.如图,矩形OABC的边OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交正半轴于一点,则这个点表示的实数是( )
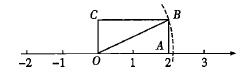
A.25 B.![]() C.
C.![]() D.
D.![]()
4.已知函数![]() 是反比例函数,则此反比例函数的图象在( )
是反比例函数,则此反比例函数的图象在( )
A.第一、三象限 B.第二、四象限
C.第一、四象限 D.第二、三象限
5.芝麻的用途广泛,经测算,一粒芝麻约有0. 00000201千克. 数据0. 00000201用科学记数法表示为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.下列交通标志既是中心对称图形又是轴对称图形的是( )
A. B.
B. C.
C. D.
D.
7.下列关系式中,不是函数关系的是( )
A.y=![]() (x<0) B.y=±
(x<0) B.y=±![]() (x>0) C.y=
(x>0) C.y=![]() (x>0) D.y=﹣
(x>0) D.y=﹣![]() (x>0)
(x>0)
8.若直线y=kx+b经过第一、二、四象限,则直线y=bx+k的图象大致是( )
A.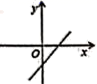 B.
B.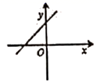 C.
C.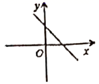 D.
D.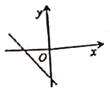
9.一次函数y=kx+b的图象如图所示,则一元一次不等式kx+b<0的解集为( )
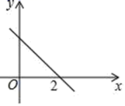
A.x<2 B.x>2 C.x<0 D.x>0
10.若一个直角三角形的两直角边长分别为3和4,则下列说法不正确的是( )
A.这个直角三角形的斜边长为5
B.这个直角三角形的周长为12
C.这个直角三角形的斜边上的高为![]()
D.这个直角三角形的面积为12
二、填空题(本大题共有6小题,每小题3分,共18分)
11.在直角ΔABC中,∠BAC=90°,AC=3,∠B=30°,点D在BC上,若ΔABD为等腰三角形,则BD=___________.
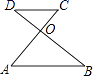
12.如图,线段AC、BD交于点O,请你添加一个条件:________,使△AOB∽△COD.
13.当x________时,分式![]() 有意义.
有意义.
14.已知![]() ,
,![]() ,则代数式
,则代数式![]() 的值为________.
的值为________.
15.使![]() 为整数的
为整数的![]() 的值可以是________(只需填一个).
的值可以是________(只需填一个).
16.下表记录了某校篮球队队员的年龄分布情况,则该校篮球队队员的平均年龄为_____.
年龄/岁 | 12 | 13 | 14 | 15 |
人数 | 1 | 3 | 4 | 2 |
三、解下列各题(本大题共8小题,共72分)
17.(8分)在菱形ABCD中,∠ABC=60°,P是射线BD上一动点,以AP为边向右侧作等边△APE,连接CE.
(1)如图1,当点P在菱形ABCD内部时,则BP与CE的数量关系是 ,CE与AD的位置关系是 .
(2)如图2,当点P在菱形ABCD外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由;
(3)如图2,连接BE,若AB=2![]() ,BE=2
,BE=2![]() ,求AP的长.
,求AP的长.

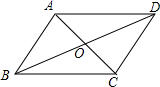
18.(8分)如图,已知平行四边形ABCD的对角线AC和BD交于点O,且AC+BD=28,BC=12,求△AOD的周长.
19.(8分)已知直线 y=kx+b(k≠0)过点 F(0,1),与抛物线 ![]() 相交于B、C 两点
相交于B、C 两点
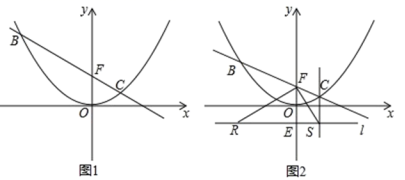
(1)如图 1,当点 C 的横坐标为 1 时,求直线 BC 的解析式;
(2)在(1)的条件下,点 M 是直线 BC 上一动点,过点 M 作 y 轴的平行线,与抛物线交于点 D, 是否存在这样的点 M,使得以 M、D、O、F 为顶点的四边形为平行四边形?若存在,求出点 M 的坐标;若不存在,请说明理由;
(3)如图 2,设 B(m,n)(m<0),过点 E(0,-1)的直线 l∥x 轴,BR⊥l 于 R,CS⊥l 于 S,连接 FR、FS.试判断△ RFS 的形状,并说明理由.
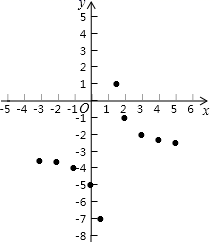
20.(8分)有这样一个问题:探究函数![]() 的图象与性质.
的图象与性质.
小亮根据学习函数的经验,对函数![]() 的图象与性质进行了探究。
的图象与性质进行了探究。
下面是小亮的探究过程,请补充完整:
(1)函数![]() 中自变量x的取值范围是_________.
中自变量x的取值范围是_________.
(2)下表是y与x的几组对应值.
x | … | -3 | -2 | -1 | 0 |
|
| 2 | 3 | 4 | 5 | … |
y | … | - | - | -4 | -5 | -7 | m | -1 | -2 | - | - | … |
求m的值;
(3)在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(4)根据画出的函数图象,发现下列特征:该函数的图象与直线x=1越来越靠近而永不相交,该函数的图象还与直线_________越来越靠近而永不相交.
21.(8分)考虑下面两种移动电话计费方式
| 方式一 | 方式二 |
月租费(月/元) | 30 | 0 |
本地通话费(元/分钟) | 0.30 | 0.40 |
(1)直接写出两种计费方式的费用y(单位:元)关于本地通话时间x(单位:分钟)的关系式.
(2)求出两种计费方式费用相等的本地通话时间是多少分钟.
22.(10分)先化简![]() ,然后在0、±1、±2这5个数中选取一个作为x的值代入求值.
,然后在0、±1、±2这5个数中选取一个作为x的值代入求值.
23.(10分)如图,在![]() ABCD中,对角线AC,BD交于点O,过点B作BE⊥CD于点E,延长CD到点F,使DF=CE,连接AF.
ABCD中,对角线AC,BD交于点O,过点B作BE⊥CD于点E,延长CD到点F,使DF=CE,连接AF.
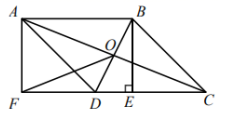
(1)求证:四边形ABEF是矩形;
(2)连接OF,若AB=6,DE=2,∠ADF=45°,求OF的长度.
24.(12分)如图,正方形ABCD和正方形CEFC中,点D在CG上,BC=1,CE=3,H是AF的中点,EH与CF交于点O.
(1)求证:HC=HF.
(2)求HE的长.
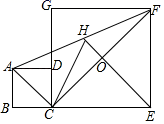
参考答案
一、选择题(每小题3分,共30分)
1、D
2、A
3、D
4、A
5、C
6、C
7、B
8、A
9、B
10、D
二、填空题(本大题共有6小题,每小题3分,共18分)
11、3或![]()
12、OB=OD.(答案不唯一)
13、![]()
14、![]()
15、1.
16、13.1.
三、解下列各题(本大题共8小题,共72分)
17、(1)BP=CE,CE⊥AD;(2)结论仍然成立,理由见解析;(3)2![]()
18、1
19、(1)![]() ;(2)存在;M点坐标为:(-3,
;(2)存在;M点坐标为:(-3,![]() ),
),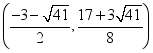 ,
,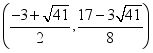 ;(3)△RFS是直角三角形;证明见详解.
;(3)△RFS是直角三角形;证明见详解.
20、 (1)![]() ;(2)1;(2)见解析;(4)y=-2.
;(2)1;(2)见解析;(4)y=-2.
21、(1)方式一y=0.3x+30,方式二y=0.4x;(2)300分钟.
22、![]() ,-
,-![]()
23、 (1)见解析;(2) OF =![]() .
.
24、(1)见解析;(2)HE=![]() .
.
2023-2024学年山西省运城市芮城县数学九上期末考试模拟试题含答案: 这是一份2023-2024学年山西省运城市芮城县数学九上期末考试模拟试题含答案,共8页。试卷主要包含了答题时请按要求用笔,估计+1的值在,若,则的值为,如图,函数y=kx+b等内容,欢迎下载使用。
2022-2023学年山西省运城市芮城县九年级(上)期末数学试卷(含详细答案解析): 这是一份2022-2023学年山西省运城市芮城县九年级(上)期末数学试卷(含详细答案解析),共28页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年山西省运城市芮城县九年级(上)期末数学试卷(含解析): 这是一份2022-2023学年山西省运城市芮城县九年级(上)期末数学试卷(含解析),共28页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












