


2022-2023学年广东省东莞市信义学校七年级数学第二学期期末达标检测模拟试题含答案
展开2022-2023学年广东省东莞市信义学校七年级数学第二学期期末达标检测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项
1.考生要认真填写考场号和座位序号。
2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。
3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。
一、选择题(每小题3分,共30分)
1.在□ABCD中,∠A:∠B=7:2,则∠C等于( )
A.40° B.80° C.120° D.140°
2.如图,矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴的正半轴于M,则点M的表示的数为( )
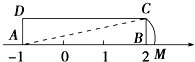
A.(2,0) B.(![]() ,0) C.(
,0) C.(![]() ,0) D.(
,0) D.(![]() ,0)
,0)
3.如图,有一块菱形纸片ABCD,沿高DE剪下后拼成一个矩形,矩形的相邻两边DC和DE的长分别是5,1.则EB的长是( )
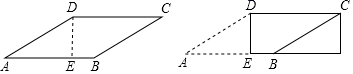
A.0.5 B.1 C.1.5 D.2
4.满足下述条件的三角形中,不是直角三角形的是![]()
![]()
A.三个内角之比为1:2:3 B.三条边长之比为1:![]() :
:![]()
C.三条边长分别为![]() ,
,![]() ,8 D.三条边长分别为41,40,9
,8 D.三条边长分别为41,40,9
5.如图,四边形ABCD是正方形,AB=1,点F是对角线AC延长线上一点,以BC、CF为邻边作菱形BEFC,连接DE,则DE的长是( ).
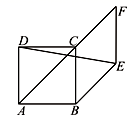
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
6.一个多边形的内角和与外角和相等,则这个多边形的边数为( )
A.8 B.6 C.5 D.4
7.下列方程是关于x的一元二次方程的是![]()
![]()
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8.如图,直线![]() 与x轴、y轴交于A、B两点,∠BAO的平分线所在的直线AM的解析式是( )
与x轴、y轴交于A、B两点,∠BAO的平分线所在的直线AM的解析式是( )
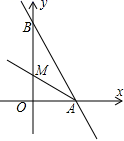
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.下列运算正确的是( )
A.![]() -
-![]() =
=![]() B.
B.![]() =2
=2![]() C.
C.![]() -
-![]() =
=![]() D.
D.![]() =2-
=2-![]()
10.如图,在△ABC中,AB=AC,AD是中线,DE⊥AB,DF⊥AC,垂足分别为E,F,则下列四个结论中:①AB上任一点与AC上任一点到D的距离相等;②AD上任一点到AB,AC的距离相等;③∠BDE=∠CDF;④∠1=∠2;其中正确的有( )
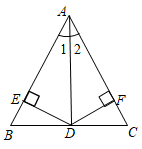
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共有6小题,每小题3分,共18分)
11.已知关于![]() 的方程
的方程![]() 会产生增根,则
会产生增根,则![]() __________.
__________.
12.若直角三角形斜边上的高和中线分别是 5 cm 和 6 cm,则面积为________,
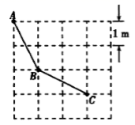
13.如图是由边长为1m的正方形地砖铺设的地面示意图,小明沿A→B→C所走的路程是____m.(结果保留根号)
14.将正比例函数![]() 的图象向上平移3个单位,所得的直线不经过第______象限.
的图象向上平移3个单位,所得的直线不经过第______象限.
15.菱形ABCD的周长为24,∠ABC=60°,以AB为腰在菱形外作底角为45°的等腰△ABE,连结AC,CE,则△ACE的面积为___________.
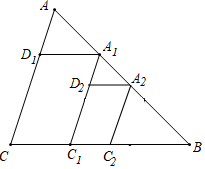
16.在△ABC中,BC=a.作BC边的三等分点C1,使得CC1:BC1=1:2,过点C1作AC的平行线交AB于点A1,过点A1作BC的平行线交AC于点D1,作BC1边的三等分点C2,使得C1C2:BC2=1:2,过点C2作AC的平行线交AB于点A2,过点A2作BC的平行线交A1C1于点D2;如此进行下去,则线段AnDn的长度为______________.
三、解下列各题(本大题共8小题,共72分)
17.(8分)在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上,请解答下列问题:
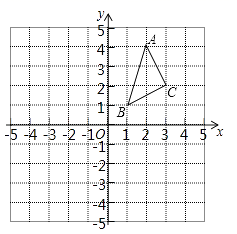
(1)①作出△ABC向左平移4个单位长度后得到的△A1B1C1, 并写出点C1的坐标;
②作出△ABC关于原点O对称的△A2B2C2, 并写出点C2的坐标;
(2)已知△ABC关于直线l对称的△A3B3C3的顶点A3的坐标为(-4,-2),请直接写出直线l的函数解析式.
18.(8分)为了绿化环境,某中学八年级(3班)同学都积极参加了植树活动,下面是今年3月份该班同学植树情况的扇形统计图和不完整的条形统计图:
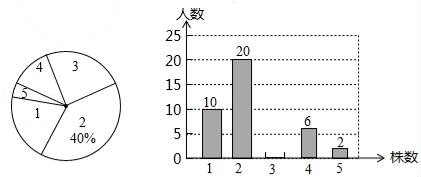
请根据以上统计图中的信息解答下列问题.
(1)植树3株的人数为 ;
(2)扇形统计图中植树为1株的扇形圆心角的度数为 ;
(3)该班同学植树株数的中位数是
(4)小明以下方法计算出该班同学平均植树的株数是:(1+2+3+4+5)÷5=3(株),根据你所学的统计知识
判断小明的计算是否正确,若不正确,请写出正确的算式,并计算出结果
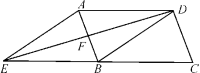
19.(8分)如图,在平行四边形ABCD中,DB=DA,∠ADB的平分线交AB于点F,交CB的延长线于点E,连接AE.
(1)求证:四边形AEBD是菱形;
(2)若DC=![]() ,EF:BF=3,求菱形AEBD的面积.
,EF:BF=3,求菱形AEBD的面积.
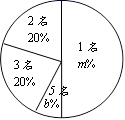
20.(8分)为了有效地落实国家精准扶贫政策,切实关爱贫困家庭学生.某校对全校各班贫困家庭学生的人数情况进行了调查.发现每个班级都有贫困家庭学生,经统计班上贫困家庭学生人数分别有1名、2名、3名、5名,共四种情况,并将其制成了如下两幅不完整的统计图:
(1)填空:a = ,b= ;
(2)求这所学校平均每班贫困学生人数;
(3)某爱心人士决定从2名贫困家庭学生的这些班级中,任选两名进行帮扶,请用列表或画树状图的方法,求出被选中的两名学生来自同一班级的概率.
贫困学生人数 | 班级数 |
1名 | 5 |
2名 | 2 |
3名 | a |
5名 | 1 |
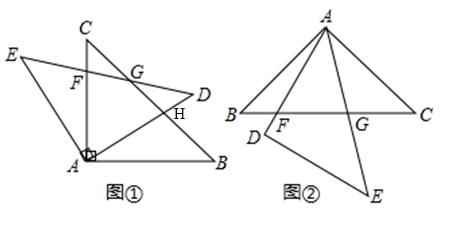
21.(8分)(1)如图①所示,将![]() 绕顶点
绕顶点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 角,得到
角,得到![]() ,
,![]() ,
,![]() 分别与
分别与![]() 、
、![]() 交于点
交于点![]() 、
、![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() .求证:
.求证:![]() ;
;
(2)如图②所示,![]() 和
和![]() 是全等的等腰直角三角形,
是全等的等腰直角三角形,![]() ,
,![]() 与
与![]() 、
、![]() 分别交于点
分别交于点![]() 、
、![]() ,请说明
,请说明![]() ,
,![]() ,
,![]() 之间的数量关系.
之间的数量关系.
22.(10分)如图,在直角坐标系中,每个小方格都是边长为![]() 的正方形,
的正方形,![]() 的顶点均在格点上,点
的顶点均在格点上,点![]() 的坐标是
的坐标是![]() .
.
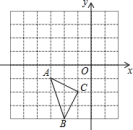
![]() 先将
先将![]() 沿
沿![]() 轴正方向向上平移
轴正方向向上平移![]() 个单位长度,再沿
个单位长度,再沿![]() 轴负方向向左平移
轴负方向向左平移![]() 个单位长度得到
个单位长度得到![]() ,画出
,画出![]() ,点
,点![]() 坐标是________;
坐标是________;
![]() 将
将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,得到
,得到![]() ,画出
,画出![]() ,并求出点
,并求出点![]() 的坐标是________;
的坐标是________;
![]() 我们发现点
我们发现点![]() 、
、![]() 关于某点中心对称,对称中心的坐标是________.
关于某点中心对称,对称中心的坐标是________.
23.(10分)数学活动课上,老师提出问题:如图,有一张长4dm,宽1dm的长方形纸板,在纸板的四个角裁去四个相同的小正方形,然后把四边折起来,做成一个无盖的盒子,问小正方形的边长为多少时,盒子的体积最大.
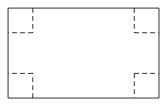
下面是探究过程,请补充完整:
(1)设小正方形的边长为x dm,体积为y dm1,根据长方体的体积公式得到y和x的关系式: ;
(2)确定自变量x的取值范围是 ;
(1)列出y与x的几组对应值.
x/dm | … |
|
|
|
|
|
|
|
|
|
| … |
y/dm1 | … | 1.1 | 2.2 | 2.7 | m | 1.0 | 2.8 | 2.5 | n | 1.5 | 0.9 | … |
(4)在下面的平面直角坐标系![]() 中,描出补全后的表中各对对应值为坐标的点,并画出该函数的图象如下图;
中,描出补全后的表中各对对应值为坐标的点,并画出该函数的图象如下图;
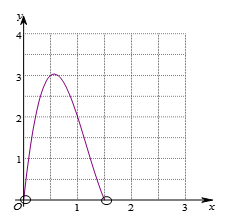
结合画出的函数图象,解决问题:
当小正方形的边长约为 dm时,(保留1位小数),盒子的体积最大,最大值约为 dm1.(保留1位小数)
24.(12分)某小区积极创建环保示范社区,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,已知温馨提示牌的单价为每个30元,垃圾箱的单价为每个90元,共需购买温馨提示牌和垃圾箱共100个.
(1)若规定温馨提示牌和垃圾箱的个数之比为1:4,求所需的购买费用;
(2)若该小区至多安放48个温馨提示牌,且费用不超过6300元,请列举所有购买方案,并说明理由.
参考答案
一、选择题(每小题3分,共30分)
1、A
2、C
3、B
4、C
5、C
6、D
7、D
8、B
9、A
10、C
二、填空题(本大题共有6小题,每小题3分,共18分)
11、4
12、30cm1
13、![]()
14、三
15、9或![]() .
.
16、![]()
三、解下列各题(本大题共8小题,共72分)
17、 (1)作图见解析,C1的坐标C1(-1,2), C2的坐标C2(-3,-2);(2)y=-x.
18、(1)12;(2)72°;(3)2;(1)小明的计算不正确,2.1.
19、(1)见解析;(2)1.
20、 (1) a=2,b=10;(2)2;(3)![]() .
.
21、(1)见解析;(1)FG1=BF1+GC1.理由见解析
22、![]() ,
, ![]() ,
, ![]() .
.
23、(1)![]() (或
(或![]() );(2)
);(2)![]() ;(1)m=1,n=2;(4)
;(1)m=1,n=2;(4)![]() ~
~![]() 都行,1~1.1都行.
都行,1~1.1都行.
24、(1)7800元;(2)购买方案为:温馨提示牌和垃圾箱个数分别为45,55;46,54;47,53;48,1.
广东省东莞市寮步镇信义学校2023-2024学年数学九上期末达标测试试题含答案: 这是一份广东省东莞市寮步镇信义学校2023-2024学年数学九上期末达标测试试题含答案,共8页。试卷主要包含了二次函数y=2-3的顶点坐标是等内容,欢迎下载使用。
广东省东莞市虎门外国语学校2023-2024学年九上数学期末达标检测模拟试题含答案: 这是一份广东省东莞市虎门外国语学校2023-2024学年九上数学期末达标检测模拟试题含答案,共7页。试卷主要包含了方程x2-x-1=0的根是等内容,欢迎下载使用。
广东省东莞市寮步镇信义学校2023-2024学年数学八上期末质量检测模拟试题含答案: 这是一份广东省东莞市寮步镇信义学校2023-2024学年数学八上期末质量检测模拟试题含答案,共6页。试卷主要包含了考生必须保证答题卡的整洁,如果代数式,下列说法正确的是等内容,欢迎下载使用。












