


2022-2023学年山东省泰安岱岳区六校联考七年级数学第二学期期末质量跟踪监视模拟试题含答案
展开2022-2023学年山东省泰安岱岳区六校联考七年级数学第二学期期末质量跟踪监视模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.答题时请按要求用笔。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题(每小题3分,共30分)
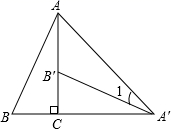
1.如图,将![]() 绕直角顶点C顺时针旋转
绕直角顶点C顺时针旋转![]() ,得到
,得到![]() ,连接
,连接![]() ,若
,若![]() ,则
,则![]() 的度数是
的度数是![]()
![]()
A.![]()
B.![]()
C.![]()
D.![]()
2.分解因式x2-4的结果是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.施工队要铺设![]() 米的下水管道,因在中考期间需停工
米的下水管道,因在中考期间需停工![]() 天,每天要比原计划多施工
天,每天要比原计划多施工![]() 米才能按时完成任务.设原计划每天施工
米才能按时完成任务.设原计划每天施工![]() 米,所列方程正确的是( )
米,所列方程正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
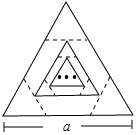
4.边长为a的等边三角形,记为第1个等边三角形,取其各边的三等分点,顺次连接得到一个正六边形,记为第1个正六边形,取这个正六边形不相邻的三边中点,顺次连接又得到一个等边三角形,记为第2个等边三角形,取其各边的三等分点,顺次连接又得到一个正六边形,记为第2个正六边形(如图),…,按此方式依次操作,则第6个正六边形的边长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.某中学随机地调查了50名学生,了解他们一周在校的体育锻炼时间,结果如下表所示:
时间(小时) | 5 | 6 | 7 | 8 |
人数 | 10 | 15 | 20 | 5 |
则这50名学生这一周在校的平均体育锻炼时间是( )
A.6.2小时 B.6.4小时 C.6.5小时 D.7小时
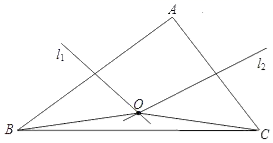
6.如图,在△ABC中,AB、AC的垂直平分线l1、l2相交于点O,若∠BAC等于82°,则∠OBC等于( )
A.8° B.9° C.10° D.11°
7.如图,![]() 中,
中,![]() 平分
平分![]() ,则
,则![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.已知点A(﹣2,y1),点B(﹣4,y2)在直线y=﹣2x+3上,则( )
A.y1>y2 B.y1=y2 C.y1<y2 D.无法比较
9.若![]() 在实数范围内有意义,则a的取值范围是( )
在实数范围内有意义,则a的取值范围是( )
A.a≥![]() B.a≤
B.a≤![]() C.a>
C.a>![]() D.a<
D.a<![]()
10.估计![]() 的运算结果在哪两个整数之间( )
的运算结果在哪两个整数之间( )
A.3和4 B.4和5 C.5和6 D.6和7
二、填空题(本大题共有6小题,每小题3分,共18分)
11.已知一次函数y=kx+b(k≠0)的图象过点(2,0),且与两坐标轴围成的三角形的面积为1,则这个一次函数的解析式是_____.
12.已知线段a,b,c能组成直角三角形,若a=3,b=4,则c=_____.
13.小明对自己上学路线的长度进行了20次测量,得到20个数据x1,x2,…,x20,已知x1+x2+…+x20=2019,当代数式(x﹣x1)2+(x﹣x2)2+…+(x﹣x20)2取得最小值时,x的值为___________.
14.若关于x的二次方程(m+1)x2+5x+m2-3m=4的常数项为0,则m的值为______.
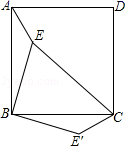
15.如图,点E是正方形ABCD内的一点,连接AE、BE、CE,将△ABE绕点B顺时针旋转90°到△CBE′的位置.若AE=1,BE=2,CE=3,则∠BE′C= 度.
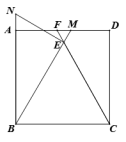
16.如图,矩形![]() 中,
中,![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,
,![]() ,则
,则![]() =_________.
=_________.
三、解下列各题(本大题共8小题,共72分)
17.(8分)某水果店经销进价分别为![]() 元/千克、
元/千克、![]() 元/千克的甲、乙两种水果,下表是近两天的销售情况:(进价、售价均保持不变,利润=售价-进价)
元/千克的甲、乙两种水果,下表是近两天的销售情况:(进价、售价均保持不变,利润=售价-进价)
时间 | 甲水果销量 | 乙水果销量 | 销售收入 |
周五 |
|
|
|
周六 |
|
|
|
(1)求甲、乙两种水果的销售单价;
(2)若水果店准备用不多于![]() 元的资金再购进两种水果共
元的资金再购进两种水果共![]() 千克,求最多能够进甲水果多少千克?
千克,求最多能够进甲水果多少千克?
(3)在(2)的条件下,水果店销售完这![]() 千克水果能否实现利润为
千克水果能否实现利润为![]() 元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
18.(8分)阅读下列题目的解题过程:
已知![]() 为
为![]() 的三边,且满足
的三边,且满足![]() ,试判断
,试判断![]() 的形状.
的形状.
解:∵![]() ①
①
∴![]() ②
②
∴![]() ③
③
∴![]() 是直角三角形
是直角三角形
问:(1)上述解题过程,从哪一步开始出现错误?请写出该步的代号: ;
(2)该步正确的写法应是: ;
(3)本题正确的结论为: .
19.(8分)先化简,再求![]() 的值,其中x=2
的值,其中x=2
20.(8分)已知,如图,在![]() ABCD中,E、F是对角线AC上的两点,且AE=CF,
ABCD中,E、F是对角线AC上的两点,且AE=CF,
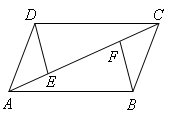
求证:DE=BF
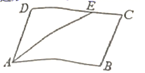
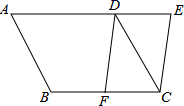
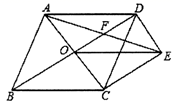
21.(8分)如图,将平行四边形ABCD的AD边延长至点E,使DE=![]() AD,连接CE,F是BC边的中点,连接FD.求证:四边形CEDF是平行四边形.
AD,连接CE,F是BC边的中点,连接FD.求证:四边形CEDF是平行四边形.
22.(10分)已知四边形ABCD的对角线AC与BD交于点O,给出下列四个论断:
①OA=OC,②AB=CD,③∠BAD=∠DCB,④AD∥BC.
请你从中选择两个论断作为条件,以“四边形ABCD为平行四边形”作为结论,完成下列各题:
(1)构造一个真命题,画图并给出证明;
(2)构造一个假命题,举反例加以说明.
23.(10分)如图,菱形![]() 的对角线
的对角线![]() 、
、![]() 相交于点
相交于点![]() ,过点
,过点![]() 作
作![]() 且
且![]() ,连接
,连接![]() 、
、![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)若菱形![]() 的边长为2,
的边长为2, ![]() .求
.求![]() 的长.
的长.
24.(12分)文美书店决定用不多于20000元购进甲乙两种图书共1200本进行销售.甲、乙两种图书的进价分别为每本20元、14元,甲种图书每本的售价是乙种图书每本售价的1.4倍,若用1680元在文美书店可购买甲种图书的本数比用1400元购买乙种图书的本数少10本.
(1)甲乙两种图书的售价分别为每本多少元?
(2)书店为了让利读者,决定甲种图书售价每本降低3元,乙种图书售价每本降低2元,问书店应如何进货才能获得最大利润?(购进的两种图书全部销售完.)
参考答案
一、选择题(每小题3分,共30分)
1、C
2、C
3、A
4、A
5、B
6、A
7、B
8、C
9、A
10、C
二、填空题(本大题共有6小题,每小题3分,共18分)
11、![]() 或
或![]()
12、5或![]()
13、100.1
14、1
15、135
16、![]()
三、解下列各题(本大题共8小题,共72分)
17、(1)甲、乙两种水果的销售单价分别为![]() 元、
元、![]() 元;(2)最多购进甲水果
元;(2)最多购进甲水果![]() 千克时,采购资金不多于
千克时,采购资金不多于![]() 元;(3)在(2)的条件下水果店不能实现利润
元;(3)在(2)的条件下水果店不能实现利润![]() 元的目标.
元的目标.
18、故答案为:(1)③;(2) 当a![]() −b
−b![]() =0时,a=b;当a
=0时,a=b;当a![]() −b
−b![]() ≠0时,a
≠0时,a![]() +b
+b![]() =c
=c![]() ;(3)△ABC是直角三角形或等腰三角形或等腰直角三角形.
;(3)△ABC是直角三角形或等腰三角形或等腰直角三角形.
19、![]() ,
,![]() .
.
20、见解析
21、见解析.
22、(1)见解析;(2)见解析.
23、(1)证明见解析(1)![]()
24、(1)甲种图书售价每本28元,乙种图书售价每本20元;(2)甲种图书进货533本,乙种图书进货667本时利润最大.
2023-2024学年山东省泰安岱岳区六校联考数学八上期末统考模拟试题含答案: 这是一份2023-2024学年山东省泰安岱岳区六校联考数学八上期末统考模拟试题含答案,共7页。试卷主要包含了已知A等内容,欢迎下载使用。
山东省青岛李沧区四校联考2022-2023学年七下数学期末质量跟踪监视模拟试题含答案: 这是一份山东省青岛李沧区四校联考2022-2023学年七下数学期末质量跟踪监视模拟试题含答案,共6页。试卷主要包含了化简的结果是,兴趣小组的同学要测量树的高度等内容,欢迎下载使用。
山东省潍坊联考2022-2023学年数学七年级第二学期期末质量跟踪监视模拟试题含答案: 这是一份山东省潍坊联考2022-2023学年数学七年级第二学期期末质量跟踪监视模拟试题含答案,共7页。












