


浙江省衢州市衢江区2022-2023学年八年级下学期期末数学试题(含答案)
展开
这是一份浙江省衢州市衢江区2022-2023学年八年级下学期期末数学试题(含答案),共11页。试卷主要包含了在中,,则的大小是,统计5位学生的成绩,如图,在中,AB=AD等内容,欢迎下载使用。
![]() 2022学年第二学期八年级期末考试数学试题卷考试须知:1.全卷共有三大题,23小题,满分为100分,考试时间为90分钟.2.答题前,请用黑色字迹的钢笔或签字笔将学校、姓名、考号填写在答题卷的相应位置上,不要漏写.3.选择题的答案请用2B铅笔填涂,其它试题的答案必须使用0.5毫米及以上的黑色字迹的钢笔或签字笔书写(画图用2B铅笔).答案必须书写在答题卷上,做在试卷上无效.本次考试不允许使用计算器.一、选择题(本大题共有10小题,每小题3分,共30分,请选出一个符合题意的正确的选项填涂在答题卷内,不选、多选、错选均不给分)1.下列中国品牌新能源车的车标中,是中心对称图形的是()A.
2022学年第二学期八年级期末考试数学试题卷考试须知:1.全卷共有三大题,23小题,满分为100分,考试时间为90分钟.2.答题前,请用黑色字迹的钢笔或签字笔将学校、姓名、考号填写在答题卷的相应位置上,不要漏写.3.选择题的答案请用2B铅笔填涂,其它试题的答案必须使用0.5毫米及以上的黑色字迹的钢笔或签字笔书写(画图用2B铅笔).答案必须书写在答题卷上,做在试卷上无效.本次考试不允许使用计算器.一、选择题(本大题共有10小题,每小题3分,共30分,请选出一个符合题意的正确的选项填涂在答题卷内,不选、多选、错选均不给分)1.下列中国品牌新能源车的车标中,是中心对称图形的是()A. B.
B.![]() C.
C.![]() D.
D.![]() 2.下列式子中属于最简二次根式的是()A.
2.下列式子中属于最简二次根式的是()A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 3.下列各点在反比例函数
3.下列各点在反比例函数![]() 图象上是()A.(2,3) B.
图象上是()A.(2,3) B.![]() C.
C.![]() D.(6,-1)4.在
D.(6,-1)4.在![]() 中,
中,![]() ,则
,则![]() 的大小是()A.
的大小是()A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 5.统计5位学生的成绩(均为不同整数),错将最高分写低了1分.则一定不受影响的统计量是()A.中位数 B.方差 C.众数 D.平均数6.如图,建筑公司验收门框时要求是矩形.在
5.统计5位学生的成绩(均为不同整数),错将最高分写低了1分.则一定不受影响的统计量是()A.中位数 B.方差 C.众数 D.平均数6.如图,建筑公司验收门框时要求是矩形.在![]() 中,对角线AC,BD相交于点O,下列验收方法错误的是()
中,对角线AC,BD相交于点O,下列验收方法错误的是() A.
A.![]() B.OA=OB C.AC=BD D.OA=OC7.用反证法证明“在直角三角形中至少有一个锐角小于或等于45°”,应假设两个锐角()A.都大于45° B.都小于45° C.都不大于45° D.都不小于45°8.罕见病“脊髓性肌萎缩症”治疗用药利司扑兰口服液在2023年医保谈判中经两轮“砍价”,从63800元/瓶降至3900元/瓶,成功进入医保目录.设这两轮谈判药物价格平均下降率为x,则可列方程为()A.
B.OA=OB C.AC=BD D.OA=OC7.用反证法证明“在直角三角形中至少有一个锐角小于或等于45°”,应假设两个锐角()A.都大于45° B.都小于45° C.都不大于45° D.都不小于45°8.罕见病“脊髓性肌萎缩症”治疗用药利司扑兰口服液在2023年医保谈判中经两轮“砍价”,从63800元/瓶降至3900元/瓶,成功进入医保目录.设这两轮谈判药物价格平均下降率为x,则可列方程为()A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 9.如图,在
9.如图,在![]() 中,AB=AD.利用尺规作图作菱形ABCD.第1步:作BD的中垂线l交BD于点O.完成下述第2步作法后,不一定能作出菱形的是()
中,AB=AD.利用尺规作图作菱形ABCD.第1步:作BD的中垂线l交BD于点O.完成下述第2步作法后,不一定能作出菱形的是()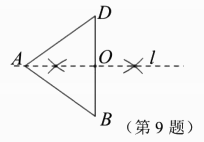 A.以D为圆心,DA的长度为半径画圆弧,交直线l于点C(A,C不重合),连结BC,CD.B.在直线l上截取OC=OA(A,C不重合),连结BC,CD.C.以B为圆心,BD的长度为半径画圆弧,交直线l于点C(在点O的右侧),连结BC,CD.D.过点D作AB的平行线,交直线l于点C,连结BC,CD.10.如图,在
A.以D为圆心,DA的长度为半径画圆弧,交直线l于点C(A,C不重合),连结BC,CD.B.在直线l上截取OC=OA(A,C不重合),连结BC,CD.C.以B为圆心,BD的长度为半径画圆弧,交直线l于点C(在点O的右侧),连结BC,CD.D.过点D作AB的平行线,交直线l于点C,连结BC,CD.10.如图,在![]() 中,CD=6,
中,CD=6,![]() ,垂足为E.点F在CE上,CF=4,连结AF,BF,点M,N分别是AF,BC的中点,连结MN,则MN的长为()
,垂足为E.点F在CE上,CF=4,连结AF,BF,点M,N分别是AF,BC的中点,连结MN,则MN的长为()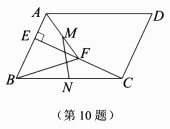 A.3 B.
A.3 B.![]() C.4 D.
C.4 D.![]() 二、填空题(本大题共有6小题,每小题3分,共18分)11.当x=______时,
二、填空题(本大题共有6小题,每小题3分,共18分)11.当x=______时,![]() 的值最小.12.五边形ABCDE的内角和为______度.13.若方程
的值最小.12.五边形ABCDE的内角和为______度.13.若方程![]() (c为常数)的一个解是
(c为常数)的一个解是![]() ,则另一个解
,则另一个解![]() ______.14.如图,
______.14.如图,![]() 的面积为18,点E在BC上,点F,G在AD上,则图中阴影部分的面积为______.
的面积为18,点E在BC上,点F,G在AD上,则图中阴影部分的面积为______.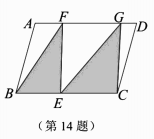 15.如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙、无重叠的四边形EFGH.若AB=4,AD=5,则BF的长为______.
15.如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙、无重叠的四边形EFGH.若AB=4,AD=5,则BF的长为______. 16.如图,已知在平面直角坐标系xOy中,
16.如图,已知在平面直角坐标系xOy中,![]() 的直角顶点A在x轴的正半轴上,点B在第一象限,OA=AB=1,反比例函数
的直角顶点A在x轴的正半轴上,点B在第一象限,OA=AB=1,反比例函数![]() 的图象分别交OB,AB于点C,D,连结CD并延长交x轴于点E.若
的图象分别交OB,AB于点C,D,连结CD并延长交x轴于点E.若![]() 的面积和
的面积和![]() 的面积相等,则:
的面积相等,则: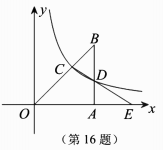 (1)
(1)![]() 的面积为______.(2)点C的坐标是______.三、解答题(本大题共有7小题,共52分请务必写出解答过程)17.(本题6分)计算:(1)
的面积为______.(2)点C的坐标是______.三、解答题(本大题共有7小题,共52分请务必写出解答过程)17.(本题6分)计算:(1)![]() (2)
(2)![]() .18.(本题6分)解方程:(1)
.18.(本题6分)解方程:(1)![]() (2)
(2)![]() .19.(本题6分)已知:如图,E,F分别是
.19.(本题6分)已知:如图,E,F分别是![]() 的边AB,CD上的点,且AE=CF.求证:四边形DEBF是平行四边形.
的边AB,CD上的点,且AE=CF.求证:四边形DEBF是平行四边形.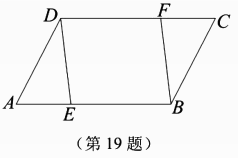 20.(本题8分)某班准备选取一名同学参加校级知识竞赛,需对甲、乙、丙三名候选人进行笔试和口试,并组织全班40名同学民主投票(无弃权且每人只能投1票,每得一票记作2分).测试成绩与得票率分别统计如下:测试项目测试成绩(分)甲乙丙笔试758084口试908080
20.(本题8分)某班准备选取一名同学参加校级知识竞赛,需对甲、乙、丙三名候选人进行笔试和口试,并组织全班40名同学民主投票(无弃权且每人只能投1票,每得一票记作2分).测试成绩与得票率分别统计如下:测试项目测试成绩(分)甲乙丙笔试758084口试908080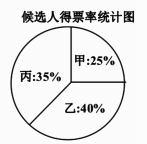 (1)请算出三人的得票分.(2)通过计算说明根据笔试、口试、投票三项得分的平均数是否可确定人选.(3)如果将笔试,口试,投票三项得分按40%,35%,25%计入个人成绩,请说明谁将被选中.21.(本题8分)某连锁超市以每支3元的价格购进某品牌牙膏,规定牙膏销售单价不低于进价又不高于5.5元,经市场调研发现,牙膏的日均销售量y(万支)与销售单价x(元)之间存在着如图所示关系.
(1)请算出三人的得票分.(2)通过计算说明根据笔试、口试、投票三项得分的平均数是否可确定人选.(3)如果将笔试,口试,投票三项得分按40%,35%,25%计入个人成绩,请说明谁将被选中.21.(本题8分)某连锁超市以每支3元的价格购进某品牌牙膏,规定牙膏销售单价不低于进价又不高于5.5元,经市场调研发现,牙膏的日均销售量y(万支)与销售单价x(元)之间存在着如图所示关系.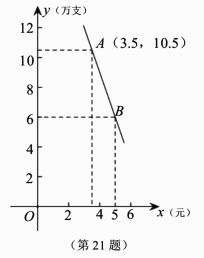 (1)求牙膏的日均销售量y(万支)关于销售单价x(元)的函数表达式(写出x的取值范围).(2)若该连锁超市想要获得9万元的日均销售利润,牙膏的销售单价应定为多少元?(3)该超市日均销售利润能否达到13万元?请说明理由.22.(本题8分)【思路点拨】如图1,点
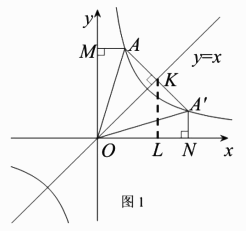
(1)求牙膏的日均销售量y(万支)关于销售单价x(元)的函数表达式(写出x的取值范围).(2)若该连锁超市想要获得9万元的日均销售利润,牙膏的销售单价应定为多少元?(3)该超市日均销售利润能否达到13万元?请说明理由.22.(本题8分)【思路点拨】如图1,点![]() 是点A关于直线y=x的对称点,分别过点A,
是点A关于直线y=x的对称点,分别过点A,![]() 作y轴,x轴的垂线,垂足为M,N,连结OA,
作y轴,x轴的垂线,垂足为M,N,连结OA,![]() ,
,![]() .可以利用轴对称图形的性质证明
.可以利用轴对称图形的性质证明![]() ≌
≌![]() ,从而由点A的坐标可求点
,从而由点A的坐标可求点![]() 的坐标.【应用拓展】如图2,若点A横坐标为
的坐标.【应用拓展】如图2,若点A横坐标为![]() ,且在函数
,且在函数![]() 的图象上.
的图象上.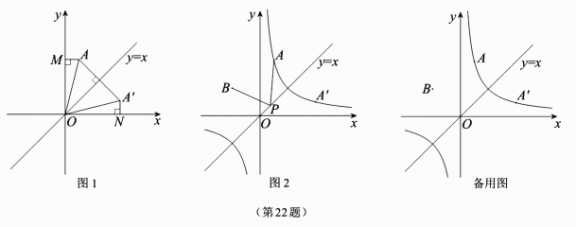 (1)求点A关于直线y=x的对称点
(1)求点A关于直线y=x的对称点![]() 的坐标.(2)若点B的坐标为(-1,1),点P是直线y=x.上的任意一点,连结AP,BP,求AP+BP的最小值.23.(本题10分)如图1,已知正方形ABCD和正方形AEFG,点E在DA的延长线上,点G在边AB上.(1)求证:
的坐标.(2)若点B的坐标为(-1,1),点P是直线y=x.上的任意一点,连结AP,BP,求AP+BP的最小值.23.(本题10分)如图1,已知正方形ABCD和正方形AEFG,点E在DA的延长线上,点G在边AB上.(1)求证:![]() ≌
≌![]() .(2)现将正方形AEFG绕点A按顺时针方向旋转
.(2)现将正方形AEFG绕点A按顺时针方向旋转![]() 度
度![]() ,在旋转过程中,探究下列问题.①当正方形AEFG旋转至图2位置时,DG分别交AB,BE于点M,N.求证:
,在旋转过程中,探究下列问题.①当正方形AEFG旋转至图2位置时,DG分别交AB,BE于点M,N.求证:![]() .②若
.②若![]() ,AG=1,当正方形AEFG的顶点(点A除外)在直线AC上时,求DG的长度.
,AG=1,当正方形AEFG的顶点(点A除外)在直线AC上时,求DG的长度.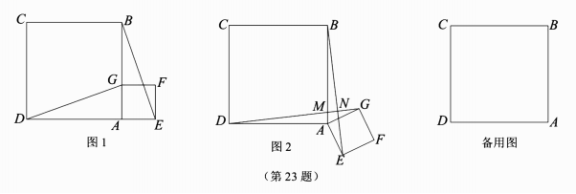 衢州市2022学年第二学期八年级学习情况调研试卷数学评分标准一、选择题:本大题有10个小题,每小题3分,共30分.1.B 2.B 3.A 4.C 5.A 6.D 7.A 8.D 9.C 10.B二、填空题:本大题有6个小题,每小题3分,共18分.11.1.12.540.13.0 14.9 15.1或4(只答对一个给2分)16.(1)
衢州市2022学年第二学期八年级学习情况调研试卷数学评分标准一、选择题:本大题有10个小题,每小题3分,共30分.1.B 2.B 3.A 4.C 5.A 6.D 7.A 8.D 9.C 10.B二、填空题:本大题有6个小题,每小题3分,共18分.11.1.12.540.13.0 14.9 15.1或4(只答对一个给2分)16.(1)![]() (2)
(2) (第(1)题1分,第(2)题2分)三、解答题:本大题有7个小题,共52分.17.(本题满分6分)解:(1)
(第(1)题1分,第(2)题2分)三、解答题:本大题有7个小题,共52分.17.(本题满分6分)解:(1)![]()
![]()
![]() (2)
(2)![]()
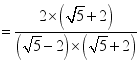
![]() 18.(本题满分6分)解:(1)∵a=2,b=3,c=-1,
18.(本题满分6分)解:(1)∵a=2,b=3,c=-1,![]() ,∴
,∴![]() ,∴
,∴![]() ,
,![]() .(2)
.(2)![]() ∴
∴![]() ,∴
,∴![]() 19.(本题满分6分)证明:∵四边形ABCD是平行四边形,∴
19.(本题满分6分)证明:∵四边形ABCD是平行四边形,∴![]() ,即
,即![]() ,AB=CD.∵AE=CF,∴AB-AE=CD-CF,即BE=DF.∴四边形DEBF是平行四边形.
,AB=CD.∵AE=CF,∴AB-AE=CD-CF,即BE=DF.∴四边形DEBF是平行四边形.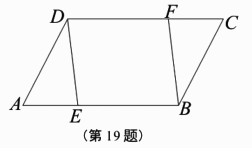 20.(本题满分 8分)解:(1)甲20分,乙32分,丙28分.(2)甲
20.(本题满分 8分)解:(1)甲20分,乙32分,丙28分.(2)甲![]() 分,乙64(即
分,乙64(即![]() )分,丙64(即
)分,丙64(即![]() )分,乙和丙的平均分相同,无法确定人选.(3)甲:75×40%+90×35%+20×25%=30+31.5+5=66.5(分).乙:80×40%+80×35%+32×25%=32+28+8=68(分).丙:84×40%+80×35%+28×25%=33.6+28+7=68.6(分).所以丙被选中.21.(本题满分8分)解:(1)设函数表达式为y=kx+b,把(3.5,10.5),(5,6)代入表达式得:
)分,乙和丙的平均分相同,无法确定人选.(3)甲:75×40%+90×35%+20×25%=30+31.5+5=66.5(分).乙:80×40%+80×35%+32×25%=32+28+8=68(分).丙:84×40%+80×35%+28×25%=33.6+28+7=68.6(分).所以丙被选中.21.(本题满分8分)解:(1)设函数表达式为y=kx+b,把(3.5,10.5),(5,6)代入表达式得:![]() 解得:
解得:![]() ∴
∴![]() .(2)设牙膏的销售单价应定为x元,根据题意得:
.(2)设牙膏的销售单价应定为x元,根据题意得:![]() ,即
,即![]() .解得:
.解得:![]() 或
或![]() .∵
.∵![]() ∴x=4.答:牙膏的销售单价应定为4元.(3)设牙膏的销售单价应定为x元,根据题意得:
∴x=4.答:牙膏的销售单价应定为4元.(3)设牙膏的销售单价应定为x元,根据题意得:![]() ,即
,即![]() .∵
.∵![]() ,∴该超市日均销售利润不可能达到13万元.22.(本题满分8分)解:(1)如图1,分别过点A,
,∴该超市日均销售利润不可能达到13万元.22.(本题满分8分)解:(1)如图1,分别过点A,![]() 作y轴,x轴的垂线,垂足为M,N,连结OA,
作y轴,x轴的垂线,垂足为M,N,连结OA,![]() ,
,![]() .
.![]() 交直线y=x于点K.∵点A,
交直线y=x于点K.∵点A,![]() 关于直线y=x对称,∴直线y=x是线段
关于直线y=x对称,∴直线y=x是线段![]() 的中垂线.∴
的中垂线.∴![]() .∵
.∵![]() ,∴
,∴![]() (三线合一).作
(三线合一).作![]() 轴于点L,易求得
轴于点L,易求得![]() ,∴
,∴![]() .∴
.∴![]() .∵
.∵![]() ,∴
,∴![]() ≌
≌![]() .∴
.∴![]() ,OM=ON.由题意可知点A坐标为
,OM=ON.由题意可知点A坐标为![]() ,∴
,∴![]() ,OM=ON=2.∴点
,OM=ON=2.∴点![]() 坐标为
坐标为![]() .
. 如图2,连结
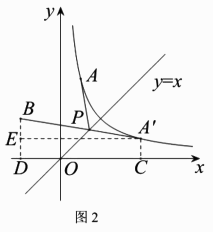
如图2,连结![]() ,交直线y=x于点P,连结AP,此时
,交直线y=x于点P,连结AP,此时![]() 为最小值(两点之间分别过点
为最小值(两点之间分别过点![]() ,B作x轴的垂线,垂足为C,D,过点
,B作x轴的垂线,垂足为C,D,过点![]() 作BD的垂线,垂足为E.∵由(1)知点
作BD的垂线,垂足为E.∵由(1)知点![]() 坐标为
坐标为![]() ,∴OC=2,
,∴OC=2,![]() .∵点B的坐标为(-1,1),∴OD=BD=1,∴CD=3.∵
.∵点B的坐标为(-1,1),∴OD=BD=1,∴CD=3.∵![]() ,∴四边形
,∴四边形![]() 是矩形.∴
是矩形.∴![]() ,
,![]() .∴
.∴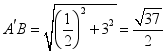 .即AP+BP的最小值为
.即AP+BP的最小值为![]() .
. 23.(本题满分10分)证明:(1)在正方形ABCD和正方形AEFG中,
23.(本题满分10分)证明:(1)在正方形ABCD和正方形AEFG中,![]() ,AD=AB,AG=AE,∴
,AD=AB,AG=AE,∴![]() ≌
≌![]() (SAS).(2)①∵∠DAB=∠GAE=90°,∴∠DAB+∠BAG=∠GAE+∠BAG,即∠DAG=∠BAE.∵AD=AB,AG=AE,∴
(SAS).(2)①∵∠DAB=∠GAE=90°,∴∠DAB+∠BAG=∠GAE+∠BAG,即∠DAG=∠BAE.∵AD=AB,AG=AE,∴![]() ≌
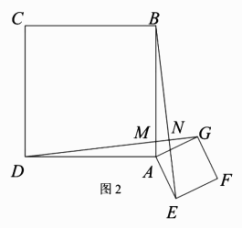
≌![]() .∴∠ADG=∠ABE.∵∠DMA=∠BMN,∴∠BNM=∠DAM=90°,∴BE⊥DG.②在正方形ABCD中,AC平分∠DAB,∴∠DAC=∠BAC=45°.Ⅰ如图3,当E在直线AC上时,过点E作EH⊥BA于点H,则∠HAE=∠CAB=45°.∵AE=AG=1,∴
.∴∠ADG=∠ABE.∵∠DMA=∠BMN,∴∠BNM=∠DAM=90°,∴BE⊥DG.②在正方形ABCD中,AC平分∠DAB,∴∠DAC=∠BAC=45°.Ⅰ如图3,当E在直线AC上时,过点E作EH⊥BA于点H,则∠HAE=∠CAB=45°.∵AE=AG=1,∴![]() ,
,![]() ,∴
,∴![]() ,∴
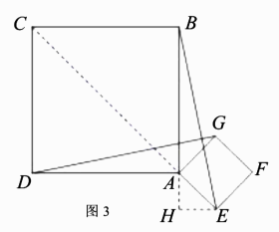
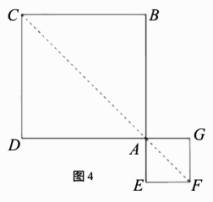
,∴![]() .Ⅱ如图4,当F在直线AC上时,在正方形AEFG中,AF平分∠EAG,∴∠EAF=∠GAF=45°.∴∠EAD=180°-∠CAD-∠EAF=90°,∠EAD+∠EAG=180°,即D,A,G三点共线.∴DG=AD+AG=
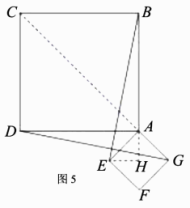
.Ⅱ如图4,当F在直线AC上时,在正方形AEFG中,AF平分∠EAG,∴∠EAF=∠GAF=45°.∴∠EAD=180°-∠CAD-∠EAF=90°,∠EAD+∠EAG=180°,即D,A,G三点共线.∴DG=AD+AG=![]() .Ⅲ如图5,当G在直线AC上,过点E作EH⊥BA于点H,则∠HAG=∠CAB=∠HAE=45°.∵AE=1,∴
.Ⅲ如图5,当G在直线AC上,过点E作EH⊥BA于点H,则∠HAG=∠CAB=∠HAE=45°.∵AE=1,∴![]() ,
,![]() .∴
.∴![]() ,∴
,∴![]() .综上所述:DG为
.综上所述:DG为![]() 或
或![]() .
.
相关试卷
这是一份浙江省衢州市衢江区2023-2024学年八年级上学期1月期末数学试题,共5页。
这是一份2023年浙江省衢州市衢江区中考二模数学试题,共9页。
这是一份2023年浙江省衢州市衢江区中考三模数学试题(含解析),共27页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。








