


2022-2023学年安徽省阜阳太和县联考数学七下期末学业质量监测模拟试题含答案
展开2022-2023学年安徽省阜阳太和县联考数学七下期末学业质量监测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
请考生注意:
1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。
2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。
一、选择题(每小题3分,共30分)
1.菱形的两条对角线长分别为12与16,则此菱形的周长是( )
A.10 B.30 C.40 D.100
2.在Rt△ABC中,斜边长AB=3,AB²+AC²+BC²的值为( )
A.18 B.24 C.15 D.无法计算
3.打开某洗衣机开关,在洗涤衣服时(洗衣机内无水),洗衣机经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间满足某种函数关系,其函数图象大致为( )
A.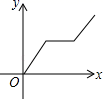 B.
B.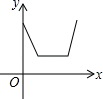
C.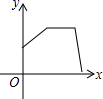 D.
D.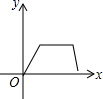
4.如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,CD⊥AB于D,则CD的长是( )
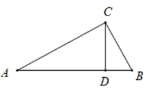
A.5 B.7 C.![]() D.
D.![]()
5.如果直线y=kx+b经过一、三、四象限,那么直线y=bx+k经过第( )象限
A.一、二、三 B.一、二、四 C.一、三、四 D.二、三、四
6.在下列各式中,(1)![]() ,(2)x2y-3xy2,(3)
,(2)x2y-3xy2,(3)![]() ,(4)
,(4)![]() ,是分式的有( )
,是分式的有( )
A.(1).(2) B.(1).(3) C.(1).(4) D.(3).(4)
7.点P(1,a),Q(﹣2,b)是一次函数y=kx+1(k<0)图象上两点,则a与b的大小关系是( )
A.a>b B.a=b C.a<b D.不能确定
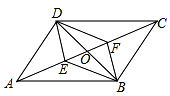
8.如图,在![]() ABCD中, 对角线AC、BD相交于点O. E、F是对角线AC上的两个不同点,当E、F两点满足下列条件时,四边形DEBF不一定是平行四边形( ).
ABCD中, 对角线AC、BD相交于点O. E、F是对角线AC上的两个不同点,当E、F两点满足下列条件时,四边形DEBF不一定是平行四边形( ).
A.AE=CF B.DE=BF C.![]() D.
D.![]()
9.下列关于变量![]() ,
,![]() 的关系,其中
的关系,其中![]() 不是
不是![]() 的函数的是( )
的函数的是( )
A.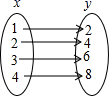 B.
B.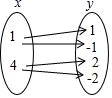
C.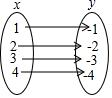 D.
D.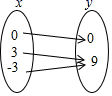
10.若关于x的分式方程![]() =1的解为正数,则m的取值范围是( )
=1的解为正数,则m的取值范围是( )
A.m>3 B.m≠-2 C.m>-3且m≠1 D.m>-3且m≠-2
二、填空题(本大题共有6小题,每小题3分,共18分)
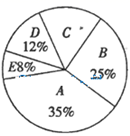
11.某中学组织八年级学生进行“绿色出行,低碳生活”知识竞赛,为了了解本次竞赛的成绩,把学生成绩分成![]() 五个等级,并绘制如图所示的扇形统计图(不完整)统计成绩,则
五个等级,并绘制如图所示的扇形统计图(不完整)统计成绩,则![]() 等级所在扇形的圆心角是_______º.
等级所在扇形的圆心角是_______º.
12.在平面直角坐标系中,已知点A(﹣![]() ,0),B(
,0),B(![]() ,0),点C在x轴上,且AC+BC=6,写出满足条件的所有点C的坐标_____.
,0),点C在x轴上,且AC+BC=6,写出满足条件的所有点C的坐标_____.
13.已知![]() ,则
,则![]() ______
______
14. 若A(x1,y1)和B(x2,y2)在反比例函数![]() 的图象上,且0<x1<x2,则y1与y2的大小关系是y1 y2;
的图象上,且0<x1<x2,则y1与y2的大小关系是y1 y2;
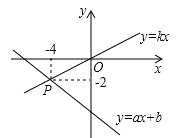
15.已知函数y=ax+b和y=kx的图象交于点P,根据图象可得,求关于x的不等式ax+b>kx的解是____________.
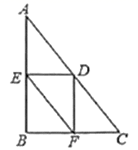
16.如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,点D是AC上的任意一点,过点D作
,点D是AC上的任意一点,过点D作![]() 于点E,
于点E,![]() 于点F,连接EF,则EF的最小值是_________.
于点F,连接EF,则EF的最小值是_________.
三、解下列各题(本大题共8小题,共72分)
17.(8分)某工厂为了解甲、乙两个部门员工的生产技能情况,从甲、乙两个部门各随机抽取20名员工,进行生产技能测试,测试成绩(百分制)如下:
甲 78 86 74 81 75 76 87 70 75 90 75 79 81 70 74 80 86 69 83 77
乙 93 73 88 81 72 81 94 83 77 83 80 81 70 81 73 78 82 80 70 40
(说明:成绩80分及以上为优秀,70-79分为良好,60-69分为合格,60分以下为不合格)
(1)请填完整表格:
部门 | 平均数 | 中位数 | 众数 |
甲 | 78.3 |
| 75 |
乙 | 78 | 80.5 |
|
(2)从样本数据可以推断出 部门员工的生产技能水平较高,请说明理由.(至少从两个不同的角度说明推断的合理性).
18.(8分)如图,在平面直角坐标系中,直线![]() 过点
过点![]() 且与
且与![]() 轴交于点
轴交于点![]() ,把点
,把点![]() 向左平移2个单位,再向上平移4个单位,得到点
向左平移2个单位,再向上平移4个单位,得到点![]() .过点
.过点![]() 且与
且与![]() 平行的直线交
平行的直线交![]() 轴于点
轴于点![]() .
.
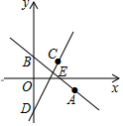
(1)求直线CD的解析式;
(2)直线AB与CD交于点E,将直线CD沿EB方向平移,平移到经过点B的位置结束,求直线CD在平移过程中与x轴交点的横坐标的取值范围.
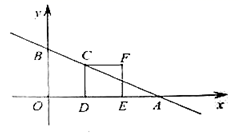
19.(8分)如图,在平面直角坐标系中,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,正方形
,正方形![]() 的点
的点![]() 在线段
在线段![]() 上,点
上,点![]() ,
,![]() 在
在![]() 轴正半轴上,点
轴正半轴上,点![]() 在点
在点![]() 的右侧,
的右侧,![]() .将正方形
.将正方形![]() 沿
沿![]() 轴正方向平移,得到正方形
轴正方向平移,得到正方形![]() ,当点
,当点![]() 与点
与点![]() 重合时停止运动.设平移的距离为
重合时停止运动.设平移的距离为![]() ,正方形
,正方形![]() 与
与![]() 重合部分的面积为
重合部分的面积为![]() .
.
(1)求直线![]() 的解析式;
的解析式;
(2)求点![]() 的坐标;
的坐标;
(3)求![]() 与
与![]() 的解析式,并直接写出自变量
的解析式,并直接写出自变量![]() 的取值范围.
的取值范围.
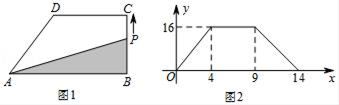
20.(8分)如图1,在直角梯形ABCD中,动点P从B点出发,沿B→C→D→A匀速运动,设点P运动的路程为x,△ABP的面积为y,图象如图2所示.
(1)在这个变化中,自变量、因变量分别是 、 ;
(2)当点P运动的路程x=4时,△ABP的面积为y= ;
(3)求AB的长和梯形ABCD的面积.
21.(8分)如图,边长为 7 的正方形 OABC 放置在平面直角坐标系中,动点 P 从点 C 出发,以 每秒 1 个单位的速度向 O 运动,点 Q 从点 O 同时出发,以每秒 1 个单位的速度向点 A 运动,到达端点即停止运动,运动时间为 t 秒,连 PQ、BP、BQ.
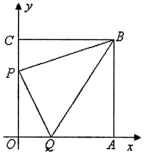
(1)写出 B 点的坐标;
(2)填写下表:
时间 t(单位:秒) | 1 | 2 | 3 | 4 | 5 | 6 |
OP 的长度 |
|
|
|
|
|
|
OQ 的长度 |
|
|
|
|
|
|
PQ 的长度 |
|
|
|
|
|
|
四边形 OPBQ 的面积 |
|
|
|
|
|
|
①根据你所填数据,请描述线段 PQ 的长度的变化规律?并猜测 PQ 长度的最小值.
②根据你所填数据,请问四边形 OPBQ 的面积是否会发生变化?并证明你的论断;
(3)设点 M、N 分别是 BP、BQ 的中点,写出点 M,N 的坐标,是否存在经过 M, N 两点的反比例函数?如果存在,求出 t 的值;如果不存在,说明理由.
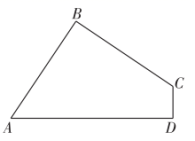
22.(10分)如图,在四边形![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,
,![]() .求证
.求证![]() .
.
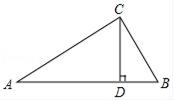
23.(10分)如图所示,在△ABC中,CD⊥AB于D,AC=4,BC=3,CD=![]() (1)求AD的长;(2)求证:△ABC是直角三角形.
(1)求AD的长;(2)求证:△ABC是直角三角形.
24.(12分)某乳品公司向某地运输一批牛奶,由铁路运输每千克需运费0.60元,由公路运输,每千克需运费0.30元,另需补助600元
(1)设该公司运输的这批牛奶为x千克,选择铁路运输时,所需运费为y1元,选择公路运输时,所需运费为y2元,请分别写出y1、y2与x之间的关系式;
(2)若公司只支出运费1500元,则选用哪种运输方式运送的牛奶多?若公司运送1500千克牛奶,则选用哪种运输方式所需费用较少?
参考答案
一、选择题(每小题3分,共30分)
1、C
2、A
3、D
4、C
5、B
6、B
7、C
8、B
9、B
10、D
二、填空题(本大题共有6小题,每小题3分,共18分)
11、72°
12、(3,0)或(﹣3,0)
13、34
14、>;
15、x<-1.
16、2.4
三、解下列各题(本大题共8小题,共72分)
17、(1)77.5,81;(2)乙,理由见解析.
18、(1)y=3x-10;(2)![]()
19、 (1)![]() ;(2)
;(2) ![]() ;(3)
;(3) 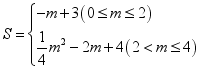 .
.
20、(1)x,y;(2)2;(3)AB=8,梯形ABCD的面积=1.
21、(1)B(7,7);(2)表格填写见解析;①,PQ长度的最小值是![]() ;
;
②四边形OPBQ的面积不会发生变化;(3)t=3.5存在经过M,N两点的反比例函数.
22、见解析
23、(1)![]() ,(2)见解析.
,(2)见解析.
24、(1)![]() ;(2)公路运输方式运送的牛奶多,铁路运输方式所需用较少.
;(2)公路运输方式运送的牛奶多,铁路运输方式所需用较少.
安徽省阜阳太和县联考2023-2024学年八上数学期末考试模拟试题含答案: 这是一份安徽省阜阳太和县联考2023-2024学年八上数学期末考试模拟试题含答案,共6页。试卷主要包含了下列计算中正确的是,已知函数和,当时,的取值范围是,下列命题的逆命题是假命题的是,下列各组值中,不是方程的解的是等内容,欢迎下载使用。
安徽省太和县联考2022-2023学年数学七下期末教学质量检测试题含答案: 这是一份安徽省太和县联考2022-2023学年数学七下期末教学质量检测试题含答案,共7页。试卷主要包含了不等式-2x>1的解集是,关于圆的性质有以下四个判断,下列说法,点P等内容,欢迎下载使用。
安徽省合肥市、安庆市名校大联考2022-2023学年七下数学期末学业质量监测模拟试题含答案: 这是一份安徽省合肥市、安庆市名校大联考2022-2023学年七下数学期末学业质量监测模拟试题含答案,共6页。试卷主要包含了考生必须保证答题卡的整洁,若有意义,则的取值范围是,函数y=中自变量x的取值范围是等内容,欢迎下载使用。













