2022-2023学年安徽省六安市七下数学期末检测试题含答案

2022-2023学年安徽省六安市七下数学期末检测试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项：

1．答卷前，考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。用2B铅笔将试卷类型（B）填涂在答题卡相应位置上。将条形码粘贴在答题卡右上角"条形码粘贴处"。

2．作答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案。答案不能答在试题卷上。

3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。不按以上要求作答无效。

4．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．某校八年级(1)班全体学生进行了第一次体育中考模拟测试，成绩统计如下表：

根据上表中的信息判断，下列结论中错误的是(   )

A．该班一共有42名同学

B．该班学生这次考试成绩的众数是8

C．该班学生这次考试成绩的平均数是27

D．该班学生这次考试成绩的中位数是27分

2．如图，四边形ABCD为平行四边形，延长AD到E，使DE＝AD，连接EB，EC，DB，下列条件中，不能使四边形DBCE成为菱形的是（　　）

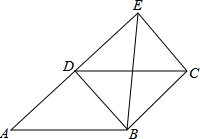
A．AB＝BE B．BE⊥DC C．∠ABE＝90° D．BE平分∠DBC

3．某特警部队为了选拔“神枪手”，举行了1000米射击比赛，最后甲、乙两名战士进入决赛，在相同条件下，两人各射靶10次，经过统计计算，甲、乙两名战士的总成绩都是99.68环，甲的方差是0.28，乙的方差是是0.1．则下列说法中，正确的是（ ）

A．甲的成绩比乙的成绩稳定 B．乙的成绩比甲的成绩稳定

C．甲、乙两人成绩的稳定性相同 D．无法确定谁的成绩更稳定

4．下列实数中,无理数是(       )

A． B． C． D．

5．如图，将一个边长分别为8，16的矩形纸片ABCD沿EF折叠，使C点与A点重合，则EF与AF的比值为（       ） 

A．4  B． C．2 D．

6．下列因式分解错误的是（　　）

A．2x（x﹣2）+（2﹣x）=（x﹣2）（2x+1） B．x2+2x+1=（x+1）2

C．x2y﹣xy2=xy（x﹣y） D．x2﹣y2=（x+y）（x﹣y）

7．若函数，则当函数值y＝8时，自变量x的值是（ ）

A．± B．4 C．±或4 D．4或－

8．函数中，自变量x的取值范围是（  ）

A． B． C． D．x为任意实数

9．如图，a，b，c分别表示苹果、梨、桃子的质量，同类水果质量相等，则下列关系正确的是

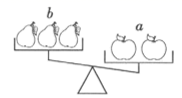
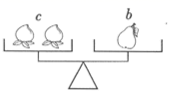
A． B． C． D．

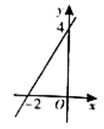
10．一次函数的图象如图所示,则不等式的解集是(　　)

A． B． C． D．

11．使等式成立的x的值是（    ）

A．是正数 B．是负数 C．是0 D．不能确定

12．在平面直角坐标系中,点关于轴的对称点在（    ）

A．第一象限 B．第二象限 C．第三象限 D．第四象限

二、填空题（每题4分，满分20分，将答案填在答题纸上）

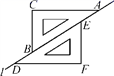
13．如图，两个完全相同的三角尺ABC和DEF在直线l上滑动．要使四边形CBFE为菱形，还需添加的一个条件是____(写出一个即可)．

14．如图,在△ABC中，AD⊥DE，BE⊥DE,AC、BC分别平分∠BAD和∠ABE．点C在线段DE上．若AD=5，BE=2，则AB的长是_____．

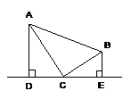
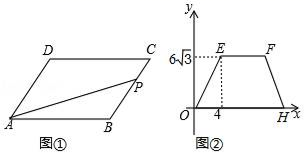
15．如图①，在▱ABCD中，∠B＝120°，动点P从点B出发，沿BC、CD、DA运动至点A停止，设点P运动的路程为xcm，△PAB的面积为ycm2，y关于x的函数的图象如图②所示，则图②中H点的横坐标为_____．

16．已知方程组，则x+y的值是____．

17．计算：﹣＝_____．

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

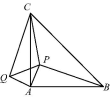
18．（5分）如图,在等腰△ABC中,∠CAB=90°,P是△ABC内一点,PA=1,PB=3,PC=,将△APB绕点A逆时针旋转后与△AQC重合.求:

(1)线段PQ的长;

(2)∠APC的度数.

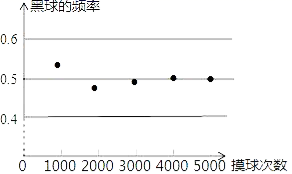
19．（5分）一个不透明的袋子里装有黑白两种颜色的球其40只，这些球除颜色外都相同．小明从袋子中随机摸一个球，记下颜色后放回，不断重复，并绘制了如图所示的统计图，根据统计图提供的信息解决下列问题：

（1）摸到黑球的频率会接近　　（精确到0.1）；

（2）估计袋中黑球的个数为　　只：

（3）若小明又将一些相同的黑球放进了这个不透明的袋子里，然后再次进行摸球试验，当重复大量试验后，发现黑球的频率稳定在0.6左右，则小明后来放进了　　个黑球．

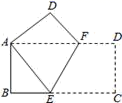
20．（8分）如图，在平面直角坐标系中，矩形OABC的顶点A，C分别在x轴，y轴的正半轴上，且OA=4，OC=3，若抛物线经过O，A两点，且顶点在BC边上，对称轴交BE于点F，点D，E的坐标分别为（3，0），（0，1）.

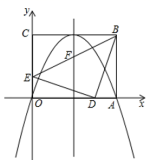
（1）求抛物线的解析式；

（2）猜想△EDB的形状并加以证明.

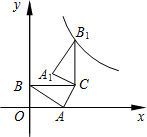
21．（10分）如图，在平面直角坐标系中，△ABC的顶点A、B分别落在x轴、y轴的正半轴上，顶点C在第一象限，BC与x轴平行．已知BC=2，△ABC的面积为1．

（1）求点C的坐标．

（2）将△ABC绕点C顺时针旋转90°，△ABC旋转到△A1B1C的位置，求经过点B1的反比例函数关系式．

22．（10分）如图，正方形ABCD中，AC是对角线，今有较大的直角三角板，一边始终经过点B，直角顶点P在射线AC上移动，另一边交DC于Q．

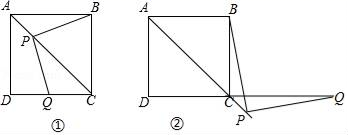
（1）如图①，当点Q在DC边上时，猜想并写出PB与PQ所满足的数量关系，并加以证明；

（2）如图②，当点Q落在DC的延长线上时，猜想并写出PB与PQ满足的数量关系，并证明你的猜想．

23．（12分）如图，在中，点、分别是、的中点，平分，交于点，交于点.

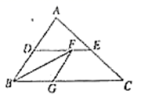
（1）求证：四边形是菱形；

（2）若，，求四边形的周长.

参考答案

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1、B

2、A

3、B

4、D

5、B

6、A

7、D

8、B

9、C

10、A

11、C

12、D

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13、CB=BF；BE⊥CF；∠EBF=60°；BD=BF等（写出一个即可）．

14、1

15、14

16、﹣1．

17、

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18、（1）；（2）135°

19、（1）0.5；（2）20；（3）10

20、（1）y=—x2+3x；（2）△EDB为等腰直角三角形，见解析.

21、（1）C（2，1）；（2）经过点B1的反比例函数为y=．

22、（1）PB＝PQ.证明见解析；（2）PB＝PQ.证明见解析.

23、（1）见解析；（2）8.