


2022-2023学年四川省遂宁市射洪县数学七年级第二学期期末质量跟踪监视试题含答案
展开2022-2023学年四川省遂宁市射洪县数学七年级第二学期期末质量跟踪监视试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
考生请注意:
1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。
2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。
3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
1.若点P(-1,3)在过原点的一条直线上,则这条直线所对应的函数解析式为( )
A.y=-3x B.y=![]() x
x
C.y=3x-1 D.y=1-3x
2.如图, ![]() OABC的顶点O,A,C的坐标分别是(0,0),(2,0),(
OABC的顶点O,A,C的坐标分别是(0,0),(2,0),(![]() ,1),则点B的坐标是( )
,1),则点B的坐标是( )
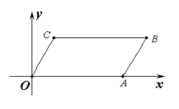
A.(1,2) B.(![]() ,2) C.(
,2) C.(![]() ,1) D.(3,1)
,1) D.(3,1)
3.若正比例函数的图像经过点![]() ,则这个图像必经过点( )
,则这个图像必经过点( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
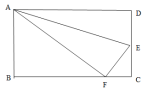
4.如图,矩形![]() 沿
沿![]() 折叠,使
折叠,使![]() 点落在
点落在![]() 边上的
边上的![]() 点处,如果
点处,如果![]() ,那么
,那么![]() 的度数是( )
的度数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.下列多项式中,不是完全平方式的是![]()
![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.下列给出的四个点中,在直线![]() 的是( )
的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
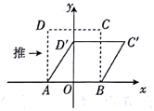
7.我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB的中点是坐标原点O,固定点A、B,把正方形沿箭头方向推,使点D落在y轴的正半轴上的点![]() 处,则点C的对应点
处,则点C的对应点![]() 的坐标为( )
的坐标为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.在直角坐标系中,点![]() 关于原点对称的点为
关于原点对称的点为![]() ,则点
,则点![]() 的坐标是( )
的坐标是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.方程 x2 x 的解是( )
A.x 1 B.x1 1 , x2 0
C.x 0 D.x1 1 , x2 0
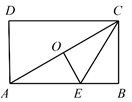
10.如图,点![]() 是矩形
是矩形![]() 两条对角线的交点,E是边
两条对角线的交点,E是边![]() 上的点,沿
上的点,沿![]() 折叠后,点
折叠后,点![]() 恰好与点
恰好与点![]() 重合.若
重合.若![]() ,则折痕
,则折痕![]() 的长为 ( )
的长为 ( )
A.![]() B.
B.![]() C.
C.![]() D.6
D.6
二、填空题(本大题共有6小题,每小题3分,共18分)
11.使![]() 有意义的x的取值范围是_____.
有意义的x的取值范围是_____.
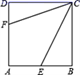
12.如图,正方形ABCD的边长为6,点E,F分别在AB,AD上,若CE=![]() ,且∠ECF=45°,则CF的长为__________.
,且∠ECF=45°,则CF的长为__________.
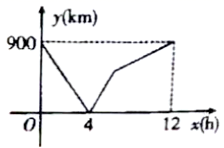
13.一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,两车的距离![]() 与慢车行驶的时间
与慢车行驶的时间![]() 之间的函数关系如图所示,则快车的速度为__________.
之间的函数关系如图所示,则快车的速度为__________.
14.关于x的一元二次方程(m﹣5)x2+2x+2=0有实根,则m的最大整数解是__.
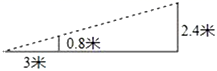
15.如图,小丽在打网球时,为使球恰好能过网(网高0.8米),且落在对方区域离网3米的位置上,已知她的击球高度是2.4米,则她应站在离网________米处.
16.如果![]() 是关于
是关于![]() 的方程
的方程![]() 的增根,那么实数
的增根,那么实数![]() 的值为__________
的值为__________
三、解下列各题(本大题共8小题,共72分)
17.(8分)如图,矩形OABC的顶点与坐标原点O重合,将△OAB沿对角线OB所在的直线翻折,点A落在点D处,OD与BC相交于点E,已知OA=8,AB=4
(1)求证:△OBE是等腰三角形;
(2)求E点的坐标;
(3)坐标平面内是否存在一点P,使得以B,D,E,P为顶点的四边形是平行四边形?若存在,请直接写出P点坐标;若不存在,请说明理由.
18.(8分)通过类比联想,引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例,先阅读再解决后面的问题:
原题:如图1,点E,F分别在正方形ABCD的边BC,CD上,![]() ,连接EF,求证:EF=BE+DF.
,连接EF,求证:EF=BE+DF.
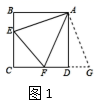
解题分析:由于AB=AD,我们可以延长CD到点G,使DG=BE,易得![]() ,可证
,可证![]() .再证明
.再证明![]() ,得EF=FG=DG+FD=BE+DF.
,得EF=FG=DG+FD=BE+DF.
问题(1):如图2,在四边形ABCD中,AB=AD,![]() ,E,F分别是边BC,CD上的点,且
,E,F分别是边BC,CD上的点,且![]() ,求证:EF=BE+FD;
,求证:EF=BE+FD;
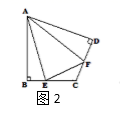
问题(2):如图3,在四边形ABCD中,![]() ,
,![]() ,AB=AD=1,点E,F分别在四边形ABCD的边BC,CD上的点,且
,AB=AD=1,点E,F分别在四边形ABCD的边BC,CD上的点,且![]() ,求此时
,求此时![]() 的周长
的周长

19.(8分)已知:如图,在正方形ABCD中,点E、F分别在BC和CD上,AE = AF
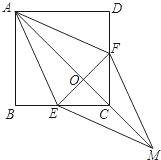
(1)求证:BE = DF;
(2)连接AC交EF于点O,延长OC至点M,使OM = OA,连接EM、FM.判断四边形AEMF是什么特殊四边形?并证明你的结论.
20.(8分)(1)先化简,再求值:![]() ,其中
,其中![]() ;
;
(2)三个数4,![]() ,
,![]() 在数轴上从左到右依次排列,求a的取值范围.
在数轴上从左到右依次排列,求a的取值范围.
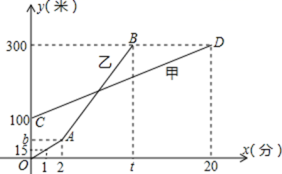
21.(8分)甲、乙两人相约周末登花果山,甲、乙两人距地面的高度![]() (米)与登山时间
(米)与登山时间![]() (分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在![]() 地时距地面的高度
地时距地面的高度![]() 为 米;
为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度![]() (米)与登山时间
(米)与登山时间![]() (分)之间的函数关系式.
(分)之间的函数关系式.
(3)登山多长时间时,甲、乙两人距地面的高度差为50米?
22.(10分)如图,已知正方形ABCD的对角线AC、BD交于点O,CE⊥AC与AD边的延长线交于点E.
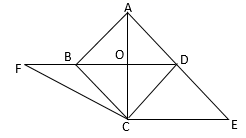
(1)求证:四边形BCED是平行四边形;
(2)延长DB至点F,联结CF,若CF=BD,求∠BCF的大小.
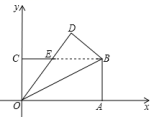
23.(10分)如图,在平面直角坐标系中,已知点A(3,4),B(﹣3,0).

(1)只用直尺(没有刻度)和圆规按下列要求作图.
(要求:保留作图痕迹,不必写出作法)
Ⅰ)AC⊥y轴,垂足为C;
Ⅱ)连结AO,AB,设边AB,CO交点E.
(2)在(1)作出图形后,直接判断△AOE与△BOE的面积大小关系.
24.(12分)综合与探究
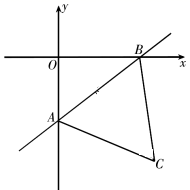
如图,在平面直角坐标系中,直线y=![]() x-3与坐标轴交于A,B两点.
x-3与坐标轴交于A,B两点.
(1)求A,B两点的坐标;
(2)以AB为边在第四象限内作等边三角形ABC,求△ABC的面积;
(3)在平面内是否存在点M,使得以M,O,A,B为顶点的四边形是平行四边形,若存在,直接写出M点的坐标:若不存在,说明理由.
参考答案
一、选择题(每小题3分,共30分)
1、A
2、C
3、B
4、C
5、D
6、D
7、A
8、B
9、B
10、A
二、填空题(本大题共有6小题,每小题3分,共18分)
11、x≥2
12、![]()
13、150km/h
14、m=1.
15、6
16、1
三、解下列各题(本大题共8小题,共72分)
17、(1)见解析; (2)(3,4); (3)(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
18、(1)![]() ,见解析;(2)
,见解析;(2)![]() 周长为
周长为![]() .
.
19、(1)证明见解析;(2)四边形AEMF是菱形,证明见解析.
20、 (1)-![]() ;(2)
;(2) ![]()
21、(1)10;1;(2)![]() ;(3)4分钟、9分钟或3分钟.
;(3)4分钟、9分钟或3分钟.
22、(1)见解析;(2)∠BCF=15°
23、(1)见解析;(2)△AOE的面积与△BOE的面积相等.
24、 (1) A(0,-3),B(4,0);(2) ![]() ;(3)存在,(-4,-3)或(4,3)或(4,-3).
;(3)存在,(-4,-3)或(4,3)或(4,-3).
四川省遂宁市遂宁市第二中学2023-2024学年数学八年级第一学期期末质量跟踪监视试题含答案: 这是一份四川省遂宁市遂宁市第二中学2023-2024学年数学八年级第一学期期末质量跟踪监视试题含答案,共8页。试卷主要包含了下列计算中,正确的是,下列等式变形中,不正确的是等内容,欢迎下载使用。
四川省阆中学2022-2023学年数学七年级第二学期期末质量跟踪监视模拟试题含答案: 这是一份四川省阆中学2022-2023学年数学七年级第二学期期末质量跟踪监视模拟试题含答案,共7页。试卷主要包含了答题时请按要求用笔,与最接近的整数是,如图是一次函数等内容,欢迎下载使用。
2022-2023学年铜陵市数学七年级第二学期期末质量跟踪监视试题含答案: 这是一份2022-2023学年铜陵市数学七年级第二学期期末质量跟踪监视试题含答案,共7页。试卷主要包含了已知一组数据,下列二次根式是最简二次根式的是,若有意义,则的取值范围是等内容,欢迎下载使用。













