


2022-2023学年四川省达州市达川区数学七年级第二学期期末联考试题含答案
展开
这是一份2022-2023学年四川省达州市达川区数学七年级第二学期期末联考试题含答案,共7页。
2022-2023学年四川省达州市达川区数学七年级第二学期期末联考试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 请考生注意:1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.不列调查方式中,最合适的是( )A.调查某品牌电脑的使用寿命,采用普查的方式B.调查游客对某国家5A级景区的满意程度情况,采用抽样调查的方式C.调查“神舟七号”飞船的零部件质量情况,采用抽样调查的方式D.调查苏州地区初中学生的睡眠时间,采用普查的方式2.设直角三角形的两条直角边长及斜边上的高分别为a,b及h,则下列关系正确的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 3.已知一次函数y=kx+b的图象如图,则k、b的符号是( )
3.已知一次函数y=kx+b的图象如图,则k、b的符号是( )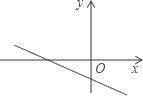 A.k>0,b>0 B.k>0,b<0 C.k<0,b>0 D.k<0,b<04.为了研究特殊四边形,李老师制作了这样一个教具(如图1):用钉子将四根木条钉成一个平行四边形框架ABCD,并在A与C、B与D两点之间分别用一根橡皮筋拉直固定,课上,李老师右手拿住木条BC,用左手向右推动框架至AB⊥BC(如图2)观察所得到的四边形,下列判断正确的是( )
A.k>0,b>0 B.k>0,b<0 C.k<0,b>0 D.k<0,b<04.为了研究特殊四边形,李老师制作了这样一个教具(如图1):用钉子将四根木条钉成一个平行四边形框架ABCD,并在A与C、B与D两点之间分别用一根橡皮筋拉直固定,课上,李老师右手拿住木条BC,用左手向右推动框架至AB⊥BC(如图2)观察所得到的四边形,下列判断正确的是( )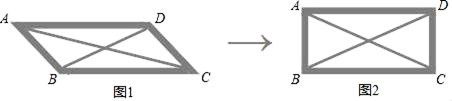 A.∠BCA=45° B.AC=BDC.BD的长度变小 D.AC⊥BD5.某水资源保护组织对邢台某小区的居民进行节约水资源的问卷调查.某居民在问卷的选项代号上画“√”,这个过程是收集数据中的( )A.确定调查范围 B.汇总调查数据C.实施调查 D.明确调查问题6.关于四边形ABCD:①两组对边分别平行;②两组对边分别相等;③有一组对边平行且相等;④对角线AC和BD相等.以上四个条件中可以判定四边形ABCD是平行四边形的有( )A.1个B.2个C.3个D.4个7.如图,直线y=x+b与直线y=kx+7交于点P(3,5),通过观察图象我们可以得到关于x的不等式x+b>kx+7的解集为x>3,这一求解过程主要体现的数学思想是( )
A.∠BCA=45° B.AC=BDC.BD的长度变小 D.AC⊥BD5.某水资源保护组织对邢台某小区的居民进行节约水资源的问卷调查.某居民在问卷的选项代号上画“√”,这个过程是收集数据中的( )A.确定调查范围 B.汇总调查数据C.实施调查 D.明确调查问题6.关于四边形ABCD:①两组对边分别平行;②两组对边分别相等;③有一组对边平行且相等;④对角线AC和BD相等.以上四个条件中可以判定四边形ABCD是平行四边形的有( )A.1个B.2个C.3个D.4个7.如图,直线y=x+b与直线y=kx+7交于点P(3,5),通过观察图象我们可以得到关于x的不等式x+b>kx+7的解集为x>3,这一求解过程主要体现的数学思想是( )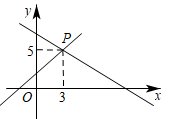 A.分类讨论 B.类比 C.数形结合 D.公理化8.一个多边形的每一个外角都等于40°,则这个多边形的内角和是.( )A.360° B.980° C.1260° D.1620°9.如图,菱形ABCD的对角线AC、BD的长分别为6和8,则这个菱形的周长是( )
A.分类讨论 B.类比 C.数形结合 D.公理化8.一个多边形的每一个外角都等于40°,则这个多边形的内角和是.( )A.360° B.980° C.1260° D.1620°9.如图,菱形ABCD的对角线AC、BD的长分别为6和8,则这个菱形的周长是( )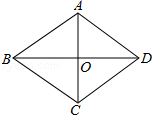 A.20 B.24 C.40 D.4810.如图,直线y1=kx+b过点A(0,2),且与直线y2=mx交于点P(1,m),则不等式组
A.20 B.24 C.40 D.4810.如图,直线y1=kx+b过点A(0,2),且与直线y2=mx交于点P(1,m),则不等式组![]() 的解集是( )
的解集是( )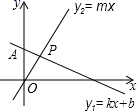 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 11. “已知:正比例函数
11. “已知:正比例函数 ![]() 与反比例函数
与反比例函数 ![]() 图象相交于
图象相交于 ![]() 两点, 其横坐标分别是 1 和﹣1,求不等式
两点, 其横坐标分别是 1 和﹣1,求不等式 ![]() 的解集.”对于这道题,某同学是这样解答的:“由图象可知:当
的解集.”对于这道题,某同学是这样解答的:“由图象可知:当![]() 或
或![]() 时,
时,![]() ,所以不等式
,所以不等式![]() 的解集是
的解集是![]() 或
或![]() ”.他这种解决问题的思路体现的数学思想方法是( )A.数形结合 B.转化 C.类比 D.分类讨论12.若
”.他这种解决问题的思路体现的数学思想方法是( )A.数形结合 B.转化 C.类比 D.分类讨论12.若![]() ,则下列不等式不成立的是( )A.
,则下列不等式不成立的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 二、填空题(每题4分,满分20分,将答案填在答题纸上)13.如图,已知Rt△ABC中,∠BCA=90°,CD是斜边上的中线,BC=12,AC=5,那么CD=_______.
二、填空题(每题4分,满分20分,将答案填在答题纸上)13.如图,已知Rt△ABC中,∠BCA=90°,CD是斜边上的中线,BC=12,AC=5,那么CD=_______.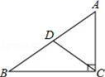 14.赵爽(约公元182~250年),我国历史上著名的数学家与天文学家,他详细解释了《周髀算经》中勾股定理,将勾股定理表述为:“勾股各自乘,并之为弦实.开方除之,即弦.”又给出了新的证明方法“赵爽弦图”,巧妙地利用平面解析几何面积法证明了勾股定理.如图所示的“赵爽弦图”是由四个全等的直角三角形和中间一个小正方形拼成的一个大正方形,如果小正方形的面积为1,直角三角形较长直角边长为4,则大正方形的面积为_____________________.
14.赵爽(约公元182~250年),我国历史上著名的数学家与天文学家,他详细解释了《周髀算经》中勾股定理,将勾股定理表述为:“勾股各自乘,并之为弦实.开方除之,即弦.”又给出了新的证明方法“赵爽弦图”,巧妙地利用平面解析几何面积法证明了勾股定理.如图所示的“赵爽弦图”是由四个全等的直角三角形和中间一个小正方形拼成的一个大正方形,如果小正方形的面积为1,直角三角形较长直角边长为4,则大正方形的面积为_____________________.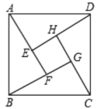 15.甲、乙两位选手各射击10次,成绩的平均数都是9.2环,方差分别是
15.甲、乙两位选手各射击10次,成绩的平均数都是9.2环,方差分别是![]() ,
,![]() ,则____选手发挥更稳定.16.如图,将边长为12的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,当两个三角形重叠部分的面积为32时,它移动的距离AA′等于________.
,则____选手发挥更稳定.16.如图,将边长为12的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,当两个三角形重叠部分的面积为32时,它移动的距离AA′等于________.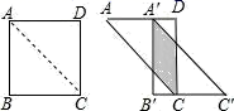 17.已知一个样本:1,3,5,x,2,它的平均数为3,则这个样本的方差是_________.三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)已知△ABC,AB=AC,D为BC上一点,E为AC上一点,AD=AE.(1)如果∠BAD=10°,∠DAE=30°,那么∠EDC= °.(2)如果∠ABC=60°,∠ADE=70°,那么∠BAD= °,∠CDE= °.(3)设∠BAD=α,∠CDE=β猜想α,β之间的关系式,并说明理由.
17.已知一个样本:1,3,5,x,2,它的平均数为3,则这个样本的方差是_________.三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)已知△ABC,AB=AC,D为BC上一点,E为AC上一点,AD=AE.(1)如果∠BAD=10°,∠DAE=30°,那么∠EDC= °.(2)如果∠ABC=60°,∠ADE=70°,那么∠BAD= °,∠CDE= °.(3)设∠BAD=α,∠CDE=β猜想α,β之间的关系式,并说明理由.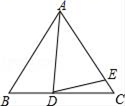 19.(5分)某班“数学兴趣小组”对函数y=x
19.(5分)某班“数学兴趣小组”对函数y=x![]() −2|x|的图象和性质进行了探究,探究过程如下,请补充完整:
−2|x|的图象和性质进行了探究,探究过程如下,请补充完整: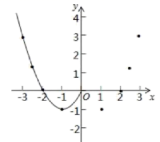 (1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下: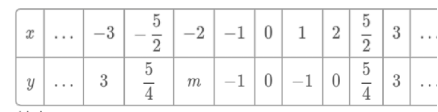 其中,m=___.(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.(3)探究函数图象发现:①函数图象与x轴有___个交点,所以对应的方程x
其中,m=___.(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.(3)探究函数图象发现:①函数图象与x轴有___个交点,所以对应的方程x![]() −2|x|=0有___个实数根;②方程x
−2|x|=0有___个实数根;②方程x![]() −2|x|=−
−2|x|=−![]() 有___个实数根;③关于x的方程x
有___个实数根;③关于x的方程x![]() −2|x|=a有4个实数根时,a的取值范围是___. 20.(8分)如图,已知一次函数的图象经过A(0,-3)、B(4,0)两点.(1)求这个一次函数的解析式; (2)若过O作OM⊥AB于M,求OM的长.
−2|x|=a有4个实数根时,a的取值范围是___. 20.(8分)如图,已知一次函数的图象经过A(0,-3)、B(4,0)两点.(1)求这个一次函数的解析式; (2)若过O作OM⊥AB于M,求OM的长.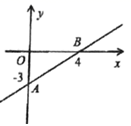 21.(10分)探究:如图,分别以△ABC的两边AB和AC为边向外作正方形ANMB和正方形ACDE,NC、BE交于点P.求证:∠ANC=∠ABE.应用:Q是线段BC的中点,若BC=6,则PQ= .
21.(10分)探究:如图,分别以△ABC的两边AB和AC为边向外作正方形ANMB和正方形ACDE,NC、BE交于点P.求证:∠ANC=∠ABE.应用:Q是线段BC的中点,若BC=6,则PQ= .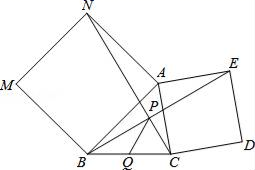 22.(10分)如图,正方形网格中的每个小正方形边长都为1,每个小正方形的顶点叫做格点.(1)以格点为顶点画
22.(10分)如图,正方形网格中的每个小正方形边长都为1,每个小正方形的顶点叫做格点.(1)以格点为顶点画![]() ,使三这长分别为
,使三这长分别为![]() ;(2)若
;(2)若![]() 的三边长分别为m、n、d,满足
的三边长分别为m、n、d,满足![]() ,求三边长,若能画出以格点为顶点的三角形,请画出该格点三角形.
,求三边长,若能画出以格点为顶点的三角形,请画出该格点三角形.
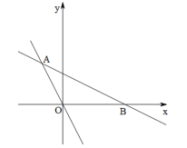
 23.(12分)如图,一次函数
23.(12分)如图,一次函数![]() 的图象与正比例函数
的图象与正比例函数![]() 的图象交于
的图象交于![]() 点,与
点,与![]() 轴交于
轴交于![]() 点,且点
点,且点![]() 的纵坐标为4,
的纵坐标为4,![]() .
. (1)求一次函数的解析式;(2)将正比例函数
(1)求一次函数的解析式;(2)将正比例函数![]() 的图象向下平移3个单位与直线
的图象向下平移3个单位与直线![]() 交于
交于![]() 点,求点
点,求点![]() 的坐标. 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、B2、A3、D4、B5、C6、C7、C8、C9、A10、A11、A12、C 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、6.514、115、甲16、1或817、1. 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)5(2)20,10(3)α=2β,理由见解析.19、(1)0;(2)见解析;(3)①3、3;②4;③0<a<−1.20、(1)y=
的坐标. 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、B2、A3、D4、B5、C6、C7、C8、C9、A10、A11、A12、C 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、6.514、115、甲16、1或817、1. 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)5(2)20,10(3)α=2β,理由见解析.19、(1)0;(2)见解析;(3)①3、3;②4;③0<a<−1.20、(1)y=![]() x-3;(2)OM=
x-3;(2)OM=![]() .21、证明见解析,322、(1)见解析如图(1);(2)三边分别为
.21、证明见解析,322、(1)见解析如图(1);(2)三边分别为![]() ,3,2是格点三角形.图见解析.23、(1)
,3,2是格点三角形.图见解析.23、(1)![]() ;(2)
;(2)![]()
相关试卷
这是一份四川省达州市达川区2023-2024学年八上数学期末统考模拟试题含答案,共8页。试卷主要包含了考生要认真填写考场号和座位序号,化简,其结果是,的相反数是,如图,已知,计算的结果是,如图,能说明的公式是等内容,欢迎下载使用。
这是一份四川省达州市达川区2023-2024学年八上数学期末检测模拟试题含答案,共8页。试卷主要包含了如图,线段关于轴对称的线段是,下图中为轴对称图形的是,下列图形中是轴对称图形的有等内容,欢迎下载使用。
这是一份四川省达州市达川区2022-2023学年七年级数学第二学期期末联考模拟试题含答案,共6页。试卷主要包含了下列分解因式,正确的是等内容,欢迎下载使用。











