2022-2023学年四川省宜宾市观音片区数学七年级第二学期期末调研模拟试题含答案

2022-2023学年四川省宜宾市观音片区数学七年级第二学期期末调研模拟试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

请考生注意：

1．请用2B铅笔将选择题答案涂填在答题纸相应位置上，请用0．5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。

2．答题前，认真阅读答题纸上的《注意事项》，按规定答题。

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．下列实数中，是方程的根的是（     ）

A．1 B．2 C．3 D．4

2．甲车行驶40km与乙车行使30km所用的时间相同，已知甲车比乙车每小时多行驶15km．设甲车的速度为xkm/h，依题意，下列所列方程正确的是（　　）

A．＝ B．＝ C．＝ D．＝

3．在一条笔直的航道上依次有甲、乙、丙三个港口，一艘船从甲出发，沿直线匀速行驶经过乙港驶向丙港，最终达到丙港，设行驶x (h)后，船与乙港的距离为y (km)，y与x的关系如图所示，则下列说法正确的是（   ）

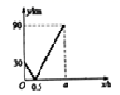
A．甲港与丙港的距离是90km B．船在中途休息了0.5小时

C．船的行驶速度是45km/h D．从乙港到达丙港共花了1.5小时

4．2022年将在北京-张家口举办冬季奥运会，很多学校开设了相关的课程．如表记录了某校4名同学短道速滑选拔赛成绩的平均数与方差：

根据表中数据，要从中选择一名成绩好又发挥稳定的运动员参加比赛，应该选择(   )

A．队员1 B．队员2 C．队员3 D．队员4

5．对于代数式（为常数），下列说法正确的是（  ）

①若，则有两个相等的实数根

②存在三个实数，使得

③若与方程的解相同，则

A．①② B．①③ C．②③ D．①②③

6．设a、b是直角三角形的两条直角边，若该三角形的周长为12，斜边长为5，则ab的值是（　　）

A．6 B．8 C．12 D．24

7．如果把分式中的、都扩大到10倍，那么分式的值（  ）

A．扩大10倍 B．不变 C．扩大20倍 D．是原来的

8．如图，已知直线y＝x与双曲线y＝ (k>0)交于A，B两点，且点A的横坐标为4.点C是双曲线上一点，且纵坐标为8，则△AOC的面积为(　　)

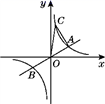
A．8 B．32 C．10 D．15

9．下列等式从左边到右边的变形，是因式分解的是（　　）

A．（3﹣a）（3+a）＝9﹣a2 B．x2﹣y2+1＝（x+y）（x﹣y）+1

C．a2+1＝a（a+） D．m2﹣2mn+n2＝（m﹣n）2

10．如图，在梯形ABCD中，∠ABC=90°，AD∥BC，AE∥CD交BC于E，∠BAE=∠EAC，O是AC的中点，AD=DC=2，下面结论：①AC=2AB；②AB=；③S△ADC=2S△ABE；④BO⊥AE，其中正确的个数是（　　）

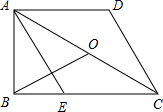
A．1 B．2 C．3 D．4

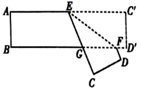
11．把一张对边互相平行的纸条，折成如图所示，是折痕，若，则下列结论正确的有是(　　)

（1）；（2）；

（3）；（4）．

A．1个 B．2个 C．3个 D．4个

12．某校将举办一场“中国汉字听写大赛”，要求每班推选一名同学参加比赛，为此，八年级（1)班组织了五轮班级选拔赛，下表记录了该班甲、乙、丙、丁四名同学五轮选拔赛成绩的平均数与方差S2：根据表中数据，要从中选择一名成绩好又发挥稳定的同学参赛，应该选择（　　）　

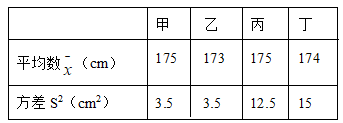
A．甲 B．乙 C．丙 D．丁

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13．与最简二次根式3是同类二次根式，则a＝_____．

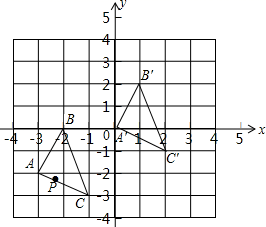
14．如图，把△ABC经过一定的变换得到△A′B′C′，如果△ABC上点P的坐标为（a，b），那么点P变换后的对应点P′的坐标为_____．

15．若分式的值为0，则__．

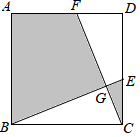
16．如图，在正方形ABCD中，AB=3，点E，F分别在CD，AD上，CE=DF，BE，CF相交于点G,若图中阴影部分的面积与正方形ABCD的面积之比为2：3，则△BCG的周长为_____．

17．将直线向右平移个单位，所得的直线的与坐标轴所围成的面积是_______.

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18．（5分）计算：

(1).

(2).

(3).

(4)解方程：.

19．（5分）在平面直角坐标系中，一次函数的图象与反比例函数（k≠0）图象交于A、B两点，与y轴交于点C，与x轴交于点D，其中A点坐标为（﹣2，3）．

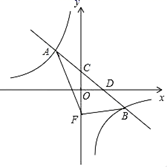
（1）求一次函数和反比例函数解析式．

（2）若将点C沿y轴向下平移4个单位长度至点F，连接AF、BF，求△ABF的面积．

（3）根据图象，直接写出不等式的解集．

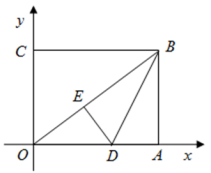
20．（8分）如图，在平面直角坐标系中，为坐标原点，矩形的顶点、，将矩形的一个角沿直线折叠，使得点落在对角线上的点处，折痕与轴交于点．

   （1）求线段的长度；

   （2）求直线所对应的函数表达式；

   （3）若点在线段上，在线段上是否存在点，使以为顶点的四边形是平行四边形？若存在，请求出点的坐标；若不存在，请说明理由．

21．（10分）已知：直线始终经过某定点．

（1）求该定点的坐标；

（2）已知，，若直线与线段相交，求的取值范围；

（3）在范围内，任取3个自变量，，，它们对应的函数值分别为，，，若以，，为长度的3条线段能围成三角形，求的取值范围．

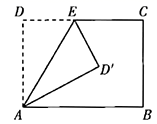
22．（10分）如图，矩形中，，，点为上一个动点，把沿折叠，当点的对应点落在的平分线上时，求的长．

23．（12分）（2013年四川广安8分）某商场筹集资金12.8万元，一次性购进空调、彩电共30台．根据市场需要，这些空调、彩电可以全部销售，全部销售后利润不少于1.5万元，其中空调、彩电的进价和售价见表格．

设商场计划购进空调x台，空调和彩电全部销售后商场获得的利润为y元．

（1）试写出y与x的函数关系式；

（2）商场有哪几种进货方案可供选择？

（3）选择哪种进货方案，商场获利最大？最大利润是多少元？

参考答案

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1、B

2、A

3、D

4、B

5、B

6、C

7、A

8、D

9、D

10、D

11、C

12、A

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13、3

14、（a+3，b+2）

15、2

16、+1．

17、

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18、 (1)-1；(2)+1；(3)；(4)x＝－15

19、（1）y＝﹣x+，y＝;(2)12;(3) x＜﹣2或0＜x＜4.

20、（1）15；（2）；（3）

21、（1）；（2）；（3）或．

22、或

23、解：（1）设商场计划购进空调x台，则计划购进彩电（30﹣x）台，由题意，得

y=（6100﹣5400）x+（3900﹣3500）（30﹣x）=300x+12000。

（2）依题意，得，

 解得10≤x≤。

∵x为整数，∴x=10，11，12。∴商场有三种方案可供选择：

方案1：购空调10台，购彩电20台；

方案2：购空调11台，购彩电19台；

方案3：购空调12台，购彩电18台。

（3）∵y=300x+12000，k=300＞0，∴y随x的增大而增大。

∴当x=12时，y有最大值，y最大=300×12+12000=15600元．

故选择方案3：购空调12台，购彩电18台时，商场获利最大，最大利润是15600元。