2022-2023学年上海民办日日学校七年级数学第二学期期末综合测试试题含答案

这是一份2022-2023学年上海民办日日学校七年级数学第二学期期末综合测试试题含答案，共7页。
2022-2023学年上海民办日日学校七年级数学第二学期期末综合测试试题（时间：120分钟             分数：120分） 学校_______            年级_______        姓名_______ 注意事项1．考生要认真填写考场号和座位序号。2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。 一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．下列各式中，一定是二次根式的有(   )个．A．2 B．3 C．4 D．52．下表记录了甲、乙、丙、丁四名同学最近几次数学考试成绩的平均数与方差： 甲乙丙丁平均数（分）92959592方差3.63.67.48.1要选择一名成绩好且发挥稳定的同学参加数学比赛，应该选择（　　）A．甲 B．乙 C．丙 D．丁3．11名同学参加数学竞赛初赛，他们的等分互不相同，按从高分录到低分的原则，取前6名同学参加复赛，现在小明同学已经知道自己的分数，如果他想知道自己能否进入复赛，那么还需知道所有参赛学生成绩的（ ）A．平均数    B．中位数    C．众数    D．方差4．已知反比例函数y=kx-1的图象过点A（1，-2），则k的值为（　　）A．1 B．2 C．-2 D．-15．为了比较甲乙两足球队的身高谁更整齐，分别量出每人身高，发现两队的平均身高一样，甲、乙两队的方差分别是1.7、2.4，则下列说法正确的是（　　）A．甲、乙两队身高一样整齐 B．甲队身高更整齐C．乙队身高更整齐 D．无法确定甲、乙两队身高谁更整齐6．不等式 的解集为（    ）.A． B． C． D．7．乒乓球是我国的国球，也是世界上流行的球类体育项目.我国乒乓球名将与其对应身高如下表所示：乒乓球名将刘诗雯邓亚萍白杨丁宁陈梦孙颖莎姚彦身高（）160155171173163160175这些乒乓球名将身高的中位数和众数是（    ）A．160，163 B．173，175 C．163，160 D．172，1608．如图，在平面直角坐标系中，以O（0，0），A（1，1），B（3，0）为顶点，构造平行四边形，下列各点中不能作为平行四边形顶点坐标的是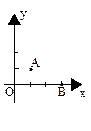（ ）A．（－3，1） B．（4，1）C．（－2，1） D．（2，－1）9．如果成立，那么实数a的取值范围是(    )A． B． C． D．10．如图，在四边形中，，对角线、相交于点O，于点E，于点F，连接、，若，则下列结论不一定正确的是（    ）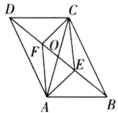A． B． C．为直角三角形 D．四边形是平行四边形11．点P是正方形ABCD边AB上一点(不与A、B重合),连接PD并将线段PD绕点P顺时针旋转90°,得线段PE,连接BE,则∠CBE等于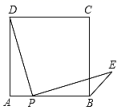（   ）A．75° B．60° C．30° D．45°12．下列各点中，不在反比例函数图象上的点是（    ）A． B． C． D．二、填空题（每题4分，满分20分，将答案填在答题纸上）13．某同学在体育训练中统计了自己五次“1分钟跳绳”成绩，并绘制了如图所示的折线统计图，这五次“1分钟跳绳”成绩的中位数是__________个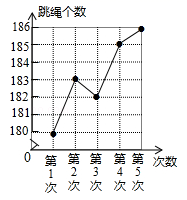．14．如果关于x的不等式组的解集是，那么m=___15．如图，函数y=2x和y=ax+4的图象相交于点A(，3)，则不等式2x＞ax+4的解集为___.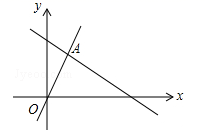16．一个装有进水管出水管的容器，从某时刻起只打开进水管进水，经过一段时间，在打开出水管放水，至15分钟时，关停进水管.在打开进水管到关停进水管这段时间内，容器内的水量y(升)与时间x（分钟）之间的关系如图所示，关停进水管后，经过_____________分钟，容器中的水恰好放完.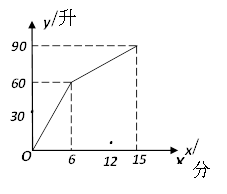17．直角三角形两条边的长度分别为3cm，4cm，那么第三条边的长度是_____cm．三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）18．（5分）如图，正方形ABCD中，点E在BC边上，AF平分∠DAE，DF//AE，AF与CD相交于点G.（1）如图1，当∠AEC = ，AE=4时，求FG的长； （2）如图2，在AB边上截取点H，使得DH=AE，DH与AF、AE分别交于点M、N，求证：AE=AH+DG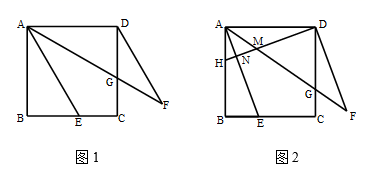   19．（5分）△ABC在平面直角坐标系xOy中的位置如图所示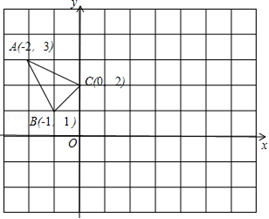．（1）作△ABC关于点C成中心对称的△A1B1C1．（2）将△A1B1C1向右平移4个单位，作出平移后的△A2B2C2．（3）在x轴上求作一点P，使PA1+PC2的值最小，并写出点P的坐标（不写解答过程，直接写出结果）   20．（8分）如图，点的纵坐标为，过点的一次函数的图象与正比例函数的图象相交于点.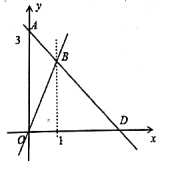（1）求该一次函数的解析式.（2）若该一次函数的图象与轴交于点，求的面积.   21．（10分）小颖和小红两位同学在做投掷骰子（质地均匀的正方体）实验，他们共做了次实验，实验的结果如下：朝上的点数出现的次数（1）计算“点朝上”的频率和“点朝上”的频率．（2）小颖说：“根据实验得出，出现点朝上的机会最大”；小红说：“如果投掷次，那么出现 点朝上的次数正好是次．”小颖和小红的说法正确吗？为什么？   22．（10分）（感知）如图①，四边形ABCD、CEFG均为正方形．可知BE=DG．（拓展）如图②，四边形ABCD、CEFG均为菱形，且∠A=∠F．求证：BE=DG．（应用）如图③，四边形ABCD、CEFG均为菱形，点E在边AD上，点G在AD延长线上．若AE=2ED，∠A=∠F，△EBC的面积为8，菱形CEFG的面积是_______．（只填结果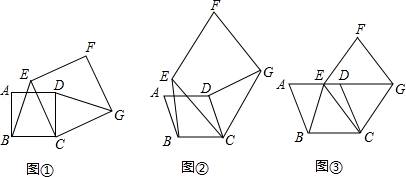）   23．（12分）已知正方形ABCD，点P是对角线AC所在直线上的动点，点E在BC边所在直线上， PE＝PB．(1)如图1，当点E在线段BC上时，求证：①PE＝PD，②PE⊥PD．简析： 由正方形的性质，图1中有三对全等的三角形，即△ABC≌△ADC，_______≌_______，和_______≌______，由全等三角形性质，结合条件中PE＝PB，易证PE＝PD．要证PE⊥PD，考虑到∠ECD = 90°，故在四边形PECD中，只需证∠PDC +∠PEC＝______即可.再结合全等三角形和等腰三角形PBE的性质，结论可证.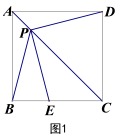(2)如图2，当点E在线段BC的延长线上时，(1)中的结论是否成立？如果成立，请给出证明；如果不成立，请说明理由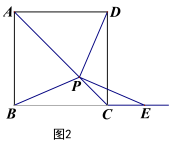；(3)若AB＝1，当△PBE是等边三角形时，请直接写出PB的长.   参考答案 一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.1、B2、B3、B4、C5、B6、B7、C8、A9、B10、C11、D12、A 二、填空题（每题4分，满分20分，将答案填在答题纸上）13、1．14、-315、x＞16、13.517、5或 三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）18、（1）FG＝2；（2）见解析.19、（1）见解析（2）见解析（3）（，0）20、（1）；（2）．21、（1）；；（2）两人的说法都是错误的，见解析.22、见解析23、 (1)△PAB；△PAD；△PBC；△PDC，180°；(2)成立，证明见解析；(3)或.