


2023年高考数学真题模拟试题专项汇编:(14)坐标系与参数方程、不等式选讲(含答案)
展开
这是一份2023年高考数学真题模拟试题专项汇编:(14)坐标系与参数方程、不等式选讲(含答案),共9页。
(14)坐标系与参数方程、不等式选讲——2023年高考数学真题模拟试题专项汇编1. 【2023年全国乙卷文科】[选修4-4:坐标系与参数方程]在直角坐标系xOy中,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() (
(![]() 为参数,
为参数,![]() ).(1)写出
).(1)写出![]() 的直角坐标方程;(2)若直线
的直角坐标方程;(2)若直线![]() 既与
既与![]() 没有公共点,也与
没有公共点,也与![]() 没有公共点,求m的取值范围.2. 【2023年全国甲卷理科】[选修4-4:坐标系与参数方程]已知点
没有公共点,求m的取值范围.2. 【2023年全国甲卷理科】[选修4-4:坐标系与参数方程]已知点![]() ,直线
,直线![]() (t为参数),
(t为参数),![]() 为l的倾斜角,l与x轴正半轴、y轴正半轴分别交于点A,B,且
为l的倾斜角,l与x轴正半轴、y轴正半轴分别交于点A,B,且![]() .(1)求
.(1)求![]() ;(2)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求l的极坐标方程.3. 【2023年全国乙卷文科】[选修4-5:不等式选讲]已知
;(2)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求l的极坐标方程.3. 【2023年全国乙卷文科】[选修4-5:不等式选讲]已知![]() .(1)求不等式
.(1)求不等式![]() 的解集;(2)在直角坐标系xOy中,求不等式组
的解集;(2)在直角坐标系xOy中,求不等式组![]() 所确定的平面区域的面积.4. 【2023年全国甲卷理科】[选修4-5:不等式选讲]设
所确定的平面区域的面积.4. 【2023年全国甲卷理科】[选修4-5:不等式选讲]设![]() ,函数
,函数![]() .(1)求不等式
.(1)求不等式![]() 的解集;(2)若曲线
的解集;(2)若曲线![]() 与x轴所围成的图形的面积为2,求a.5. 【2023年四川绵阳模拟】在平面直角坐标
与x轴所围成的图形的面积为2,求a.5. 【2023年四川绵阳模拟】在平面直角坐标![]() 中,曲线C的参数方程为
中,曲线C的参数方程为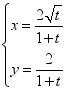 (t为参数)(1)写出曲线C的普通方程;(2)若A、B是曲线上的两点且
(t为参数)(1)写出曲线C的普通方程;(2)若A、B是曲线上的两点且![]() ,求
,求![]() 的最大值.6. 【2023年四川绵阳模拟】已知定义在R上的函数
的最大值.6. 【2023年四川绵阳模拟】已知定义在R上的函数![]() 的最大值为p.(1)求p的值;(2)设
的最大值为p.(1)求p的值;(2)设![]() ,
,![]() 求证:
求证:![]() .7. 【2023年广西省模拟】在平面直角坐标系中,曲线C的参数方程为
.7. 【2023年广西省模拟】在平面直角坐标系中,曲线C的参数方程为 (t为参数,且
(t为参数,且![]() ),曲线C与x轴交于A点,与y轴交于B.(1)求|AB|(2)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求以线段AB为直径的圆M的极坐标方程.8. 【2023年广西省模拟】已知a,b均为正实数,且
),曲线C与x轴交于A点,与y轴交于B.(1)求|AB|(2)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求以线段AB为直径的圆M的极坐标方程.8. 【2023年广西省模拟】已知a,b均为正实数,且![]() ,证明:(1)
,证明:(1)![]() ;(2)
;(2)![]() .9. 【2023年甘肃省模拟】在平面直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线
.9. 【2023年甘肃省模拟】在平面直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() (1)写出曲线
(1)写出曲线![]() 的参数方程;(2)设M是曲线
的参数方程;(2)设M是曲线![]() 上的动点,N是曲线
上的动点,N是曲线![]() 上的动点,求
上的动点,求![]() 的最大值.10. 【2023年甘肃省模拟】已知函数
的最大值.10. 【2023年甘肃省模拟】已知函数![]() .(1)求不等式
.(1)求不等式![]() 的解集;(2)已知函数
的解集;(2)已知函数![]() 的最小值为m,且a,b,c都是正数,
的最小值为m,且a,b,c都是正数,![]() ,证明:
,证明:![]() .
.
答案以及解析1.答案:(1)![]() (
(![]() ,
,![]() )(2)
)(2)![]() 解析:(1)
解析:(1)![]() ,方程两边问时乘以
,方程两边问时乘以![]() ,得
,得![]() ,将
,将![]() ,
,![]() 代入,得
代入,得![]() ,又
,又![]() ,所以
,所以![]() 的直角坐标方程为
的直角坐标方程为![]() (
(![]() ,
,![]() ).(2)由
).(2)由![]() 的参数方程可得
的参数方程可得![]() 的普通方程为
的普通方程为![]() (
(![]() ,
,![]() ).数形结合可知,若直线
).数形结合可知,若直线![]() 与
与![]() 没有公共点,则
没有公共点,则![]() 或
或![]() ;若直线
;若直线![]() 与
与![]() 没有公共点,可先求相切时的临界情况,即
没有公共点,可先求相切时的临界情况,即![]() ,得
,得![]() ,所以当
,所以当![]() 或
或![]() 时,直线
时,直线![]() 与
与![]() 没有公共点.综上,当
没有公共点.综上,当![]() 或
或![]() 时,直线
时,直线![]() 与
与![]() 和
和![]() 均没有公共点,故m的取值范围为
均没有公共点,故m的取值范围为![]() .2.答案:(1)
.2.答案:(1)![]() (2)
(2)![]() 解析:(1)记点A,B对应的参数分别为
解析:(1)记点A,B对应的参数分别为![]() ,
,![]() .令
.令![]() ,得
,得![]() ,令
,令![]() ,得
,得![]() ,则
,则![]() ,所以
,所以![]() ,由题可知
,由题可知![]() ,所以
,所以![]() 或
或![]() .因为直线l与x轴正半轴、y轴正半轴相交,所以
.因为直线l与x轴正半轴、y轴正半轴相交,所以![]() .(2)根据(1)得直线l的参数方程为
.(2)根据(1)得直线l的参数方程为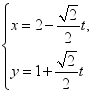 (t为参数),转化为普通方程为
(t为参数),转化为普通方程为![]() ,因为
,因为![]() ,
,![]() ,所以l的极坐标方程为
,所以l的极坐标方程为![]() .3.答案:(1)
.3.答案:(1)![]() (2)8解析:(1)
(2)8解析:(1)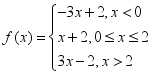 ,当
,当![]() 时,
时,![]() ,得
,得![]() ;当
;当![]() 时,
时,![]() ,得
,得![]() ;当
;当![]() 时,
时,![]() ,得
,得![]() ,与
,与![]() 矛盾.综上,不等式
矛盾.综上,不等式![]() 的解集为
的解集为![]() .(2)如图所示,作出不等式组
.(2)如图所示,作出不等式组![]() ,即
,即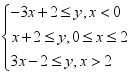 所确定的平面区域(图中阴影部分),为
所确定的平面区域(图中阴影部分),为![]() ,
,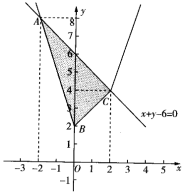 其中
其中![]() ,
,![]() ,
,![]() ,直线
,直线![]() 与y轴交于点
与y轴交于点![]() ,所以
,所以![]() .4.答案:(1)
.4.答案:(1)![]() (2)
(2)![]() 解析:解法一:(1)求不等式
解析:解法一:(1)求不等式![]() 的解集,即求不等式
的解集,即求不等式![]() 的解集,整理得
的解集,整理得![]() ,不等式两边同时平方,得
,不等式两边同时平方,得![]() ,整理得
,整理得![]() 因式分解得
因式分解得![]() ,因为
,因为![]() ,所以可得
,所以可得![]() ,故不等式的解集为
,故不等式的解集为![]() .(2)设曲线
.(2)设曲线![]() 与x轴的两个交点的横坐标分别为
与x轴的两个交点的横坐标分别为![]() ,
,![]() ,
,![]() .令
.令![]() ,得
,得![]() ,即
,即![]() 或
或![]() ,得
,得![]() ,
,![]() ,故曲线
,故曲线![]() 与x轴的两个交点之间的距离
与x轴的两个交点之间的距离![]() ,易得三角形不在x轴上的顶点的坐标为
,易得三角形不在x轴上的顶点的坐标为![]() ,所以三角形的面积
,所以三角形的面积![]() ,即
,即![]() ,解得
,解得![]() 或
或![]() (舍去),故
(舍去),故![]() .解法二:(1)若
.解法二:(1)若![]() ,则
,则![]() ,即
,即![]() ,解得
,解得![]() ,得
,得![]() ;(注:
;(注:![]() )若
)若![]() ,则
,则![]() ,解得
,解得![]() ,得
,得![]() .综上,不等式的解集为
.综上,不等式的解集为![]() .(2)
.(2)![]() ,作出
,作出![]() 的大致图象如图,曲线
的大致图象如图,曲线![]() 与x轴围成的图形即
与x轴围成的图形即![]() ,
, 易得
易得![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,
,![]() 的底边AB上的高为a,所以
的底边AB上的高为a,所以![]() ,解得
,解得![]() 或
或![]() (舍去),故
(舍去),故![]() .5.答案:(1)
.5.答案:(1)![]() (2)2解析:(1)由曲线C的参数方程为
(2)2解析:(1)由曲线C的参数方程为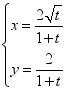 ,消去t可得:
,消去t可得:![]() .(2)因为
.(2)因为![]() 的半径为1,且A、B是曲线C上的两点,
的半径为1,且A、B是曲线C上的两点,![]() ,所以
,所以![]() ,所以
,所以![]() .不妨设点A对应的参数为
.不妨设点A对应的参数为![]() ,
,![]() ,则点B所对应的参数为
,则点B所对应的参数为![]() ,所以
,所以![]() 则
则![]() ,即点
,即点![]() .所以
.所以![]()
![]() .
.![]() ,
,![]() ,
,![]() 的最大值为
的最大值为![]() ,即当
,即当![]() ,
,![]() 时,
时,![]() 的最大值为2.6.答案:(1)
的最大值为2.6.答案:(1)![]() (2)证明见解析解析:(1)
(2)证明见解析解析:(1)![]() ,当且仅当
,当且仅当![]() 时等号成立.
时等号成立.![]() ,即
,即![]() .(2)依题意可知
.(2)依题意可知![]() ,则由柯西不等式得,
,则由柯西不等式得,![]() ,
,![]() ,即
,即![]() ,当且仅当
,当且仅当![]() 时,等号成立.7.答案:(1)
时,等号成立.7.答案:(1)![]() (2)
(2)![]() 解析:(1)令
解析:(1)令![]() ,则
,则![]() ,解得
,解得![]() 或
或![]() (舍),则
(舍),则![]() ,即
,即![]() .令
.令![]() ,则
,则![]() ,解得
,解得![]() 或
或![]() (舍),则
(舍),则![]() ,即
,即![]() .
.![]() (2)由(1)可知
(2)由(1)可知![]() ,则以线段AB为直径的圆M的半径为
,则以线段AB为直径的圆M的半径为![]() ,所以圆M的直角坐标方程为
,所以圆M的直角坐标方程为![]() .由
.由![]() ,
,![]() 可得,直线AB的极坐标方程为
可得,直线AB的极坐标方程为![]() .8.答案:(1)证明见解析(2)证明见解析解析:(1)由柯西不等式有
.8.答案:(1)证明见解析(2)证明见解析解析:(1)由柯西不等式有![]() ,又
,又![]() ,则
,则![]() ,当且仅当
,当且仅当![]() 时,取等号
时,取等号![]() .(2)
.(2)![]() ,
,![]()
![]() 又
又![]() ,
,![]() ,当且仅当
,当且仅当![]() ,即
,即![]() 时取等号,
时取等号,![]() .9.答案:(1)
.9.答案:(1)![]() (
(![]() 为参数)(2)
为参数)(2)![]() 解析:(1)由曲线
解析:(1)由曲线![]() 的极坐标方程为
的极坐标方程为![]() ,得
,得![]() ,即
,即![]() ,即
,即![]() ,所以由线
,所以由线![]() 的直角坐标方程为
的直角坐标方程为![]() 由圆锥曲线参数方程定义,得曲线
由圆锥曲线参数方程定义,得曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).(2)由曲线
为参数).(2)由曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),得曲线
为参数),得曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ,其圆心
,其圆心![]() ,半径
,半径![]() .由題意可得设
.由題意可得设![]() ,易知
,易知![]() 的最大值为点N到圆心
的最大值为点N到圆心![]() 的距离的最大值再加上半径,歫
的距离的最大值再加上半径,歫![]() ,由二次函数性质可知,当
,由二次函数性质可知,当![]() 时,
时,![]() ,所以
,所以![]() 的最大值为
的最大值为![]() .10.答案:(1)
.10.答案:(1)![]() (2)证明见解析解析:(1)当
(2)证明见解析解析:(1)当![]() 时,
时,![]() ,解得
,解得![]() ;当
;当![]() 时,则有
时,则有![]() ,解得
,解得![]() 当
当![]() 时,
时,![]() ,解得
,解得![]() .综上所述,不等式
.综上所述,不等式![]() 的解集为
的解集为![]() .(2)证明:由绝对值三角不等式可得
.(2)证明:由绝对值三角不等式可得![]() ,当且仅当
,当且仅当![]() 时,即当
时,即当![]() 时,等号成立,故
时,等号成立,故![]() ,所以
,所以![]() ,又因为a,b,c均为正数,所以
,又因为a,b,c均为正数,所以![]()
![]() 当且仅当
当且仅当![]() 时,等号成立,故
时,等号成立,故![]() .
.
相关试卷
这是一份【讲通练透】专题18 坐标系与参数方程、不等式选讲-2021-2023年高考真题分享汇编(全国通用),文件包含专题18坐标系与参数方程不等式选讲全国通用原卷版docx、专题18坐标系与参数方程不等式选讲全国通用解析版docx等2份试卷配套教学资源,其中试卷共17页, 欢迎下载使用。
这是一份三年(2021-2023)高考数学真题专项18坐标系与参数方程、不等式选讲含答案,文件包含通用版三年2021-2023高考数学真题专项18坐标系与参数方程不等式选讲含答案docx、通用版三年2021-2023高考数学真题专项18坐标系与参数方程不等式选讲docx等2份试卷配套教学资源,其中试卷共17页, 欢迎下载使用。
这是一份高考数学真题分项汇编三年(2021-2023)(全国通用)专题18+坐标系与参数方程、不等式选讲,文件包含专题18坐标系与参数方程不等式选讲全国通用解析版docx、专题18坐标系与参数方程不等式选讲全国通用原卷版docx等2份试卷配套教学资源,其中试卷共15页, 欢迎下载使用。










