


2021届高三上学期期中适应性考试数学(文)试卷 Word版含答案
展开 www.ks5u.com赣县三中2020-2021学年上学期高三期中适应性考文数试题
www.ks5u.com赣县三中2020-2021学年上学期高三期中适应性考文数试题
一、选择题(本题共12道小题,每小题5分,共60分)
1、“![]() ”是“
”是“![]() ”的( )
”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
2、若![]() ,则下列不等式成立的是( )
,则下列不等式成立的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3、若![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
4、已知向量![]() ,向量
,向量![]() ,若
,若![]() ,则实数x的值为( )
,则实数x的值为( )
A. -5 B. 5 C. -1 D. 1
5、已知函数![]() ,则其单调增区间是( )
,则其单调增区间是( )
A. (1,+∞) B. (0,+∞) C. (0,1] D. [0,1]
6、函数y=xcos x+sin x的图象大致为 ( ).
A.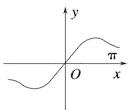 B.
B.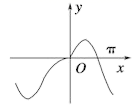
C.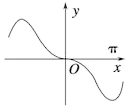 D.
D.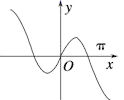
A. B. C. D.
7、设数列{an}的前n项和Sn,若![]() ,则a4=( )
,则a4=( )
A. 27 B. -27 C. ![]() D.
D. ![]()
8、已知函数![]() 是偶函数,则
是偶函数,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.0
D.0
9、已知定义在R上的函数![]() 是奇函数,且满足
是奇函数,且满足![]() ,
,![]() ,则
,则![]() ( )
( )
A .-2 B.2 C.-3 D.3
10、我国南宋著名数学家秦九韶发现了从三角形三边求三角形面积的“三斜公式”,设△ABC三个内角A,B,C所对的边分别为a,b,c,面积为S,则“三斜求积”公式为S=![]() .若a2sinC=4sinA,(a+c)2=12+b2,则用“三斜求积”公式求得△ABC的面积为( )
.若a2sinC=4sinA,(a+c)2=12+b2,则用“三斜求积”公式求得△ABC的面积为( )
A.![]() B.2 C.3 D.
B.2 C.3 D.![]()
11、已知![]() 为定义在
为定义在![]() 上的可导函数,
上的可导函数,![]() 为其导函数,且
为其导函数,且![]() 恒成立,则( )
恒成立,则( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
12.把函数![]() 的图象向右平移一个单位,所得图象与函数
的图象向右平移一个单位,所得图象与函数![]() 的图象关于直线
的图象关于直线![]() 对称;已知偶函数
对称;已知偶函数![]() 满足
满足![]() ,当
,当![]() 时,
时,![]() ;若函数
;若函数![]() 有五个零点,则
有五个零点,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(本题共4道小题,每小题5分,共20分)
13.已知实数![]() 、
、![]() 满足
满足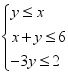 ,则
,则![]() 与
与![]() 之积的最大值为____________.
之积的最大值为____________.
14、在3与156之间插入50个数,使这52个数成等差数列,则插入的50个数的和等于________.
15、已知平面向量![]() ,
,![]() 满足
满足![]() ,
,![]() ,
,![]() ,则
,则![]() 与
与![]() 的夹角为________.
的夹角为________.
16、下列结论:①函数![]() 的图象的一条对称轴方程是
的图象的一条对称轴方程是![]() ;②
;②![]() 中,若
中,若![]() ,则
,则![]() ;③在△ABC中,内角A,B,C成等差数列,则
;③在△ABC中,内角A,B,C成等差数列,则![]() ;④已知数列{an}的通项公式为
;④已知数列{an}的通项公式为![]() ,其前n项和为Sn,当Sn取得最大值时
,其前n项和为Sn,当Sn取得最大值时![]() ,其中正确的序号是______.
,其中正确的序号是______.
三、解答题(本题共6道小题,第17题10分, 第18—22题12分,共70分) |
17、已知命题![]() :
:![]() ,
,![]() ;命题
;命题![]() :
:![]() ,
, ![]() .
.
(1)写出命题![]() 的否定;
的否定;
(2)若“![]() ”及“
”及“![]() 或
或![]() ”均为真命题,求实数
”均为真命题,求实数![]() 的取值范围.
的取值范围.
18、已知等比数列![]() 各项均为正数,
各项均为正数,![]() 是数列
是数列![]() 的前
的前![]() 项和,且
项和,且![]() ,
,![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
19、设平面向量![]() ,
,![]() ,函数
,函数![]() .
.
(1)求函数![]() 的最小正周期和单调增区间;
的最小正周期和单调增区间;
(2)当![]() 时,求函数
时,求函数![]() 的最大值和最小值.
的最大值和最小值.
20、已知![]() ,
,![]() ,
,![]() 分别为
分别为![]() 内角
内角![]() ,
,![]() ,
,![]() 的对边,且
的对边,且![]() .
.
(1)证明:![]() ,
,![]() ,
,![]() 成等差数列;
成等差数列;
(2)若![]() 的外接圆半径为
的外接圆半径为![]() ,且
,且![]() ,求
,求![]() 的面积.
的面积.
21、新冠肺炎疫情发生以后,口罩供不应求,某口罩厂日夜加班生产,为抗击疫情做贡献.生产口罩的固定成本为200万元,每生产![]() 万箱,需另投入成本
万箱,需另投入成本![]() 万元,当产量不足90万箱时,
万元,当产量不足90万箱时,![]() ;当产量不小于90万箱时,
;当产量不小于90万箱时,![]() ,若每箱口罩售价100元,通过市场分析,该口罩厂生产的口罩可以全部销售完.
,若每箱口罩售价100元,通过市场分析,该口罩厂生产的口罩可以全部销售完.
(1)求口罩销售利润![]() (万元)关于产量
(万元)关于产量![]() (万箱)的函数关系式;
(万箱)的函数关系式;
(2)当产量为多少万箱时,该口罩生产厂在生产中所获得利润最大?
22、已知函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线为
处的切线为![]() .
.
(1)求a,b的值;
(2)若对任意的![]() ,
,![]() 恒成立,求正整数m的最大值.
恒成立,求正整数m的最大值.
高三期中适应性考文数参考答案
一、选择:1-5 ABCBA 6-10 DBABA 11-12 CC
二、填空题
13.512 14.3975 15. ![]() 16.②③
16.②③
三、解答题
17、(1)命题![]() 的否定
的否定![]() 为:
为:![]() ,
,![]() .
.
(2)∵若“![]() ”及“P或q”均为真命题 ∴
”及“P或q”均为真命题 ∴![]() 为假命题,
为假命题,![]() 为真命题
为真命题
∵![]() , ∴
, ∴![]() .
.
∵![]() ,
,![]() ,可得
,可得![]() ,
,
∴![]() 或
或![]() .故命题
.故命题![]() 为真命题时,
为真命题时,![]() 或
或![]() .
.
又命题![]() :
:![]() ,
,![]() 为真, ∴
为真, ∴![]() 或
或![]() ,
,
从而命题![]() 为假命题时,
为假命题时,![]() .
.
所以命题![]() 为真命题,
为真命题,![]() 为假命题时,
为假命题时,![]() 的取值范围为
的取值范围为![]() .
.
18.(1)设等比数列![]() 的公比为
的公比为![]() ,
,
因为![]() ,
,![]() ,所以
,所以![]() ,
,
因为![]() 各项均为正数,解得
各项均为正数,解得![]() (负值舍去),
(负值舍去),
所以![]() ;
;
(2)由已知得,![]() ,
,
所以![]() 为等差数列,
为等差数列,
因为![]()
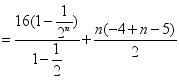 ,
,
所以![]() .
.
19、解(1)因为![]() ,
,![]() ,
,
所以![]()
![]()
![]() 故函数
故函数![]() 的最小正周期
的最小正周期![]() ,
,
由![]() 得
得![]()
![]()
![]() 。。。。。。。。。。。。。。。。。。。。。6分
。。。。。。。。。。。。。。。。。。。。。6分
(2)因为![]() ,所以
,所以![]() ,
,
故当![]() ,即
,即![]() 时,函数
时,函数![]() 取最大值,
取最大值,![]() ,
,
当![]() ,即
,即![]() 时,函数
时,函数![]() 取最小值,
取最小值,![]() .。。。。。。。。。。。。。12分
.。。。。。。。。。。。。。12分
20.(1)证明:由已知得![]() ,即
,即![]() ,
,
由余弦定理得![]() ,
,
∴![]() ,即
,即![]() ,
,![]() ,
,![]() 成等差数列.
成等差数列.
(2)由正弦定理得![]() ,
,
又因为![]() ,
,![]() 得
得![]() ,
,
由(1)知![]() 不可能是钝角,
不可能是钝角,
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() 可得
可得![]() ,
,
∴![]() 的面积为
的面积为![]() .
.
21.【详解】(1)当![]() 时,
时,
![]() ;
;
当![]() 时,
时,![]() ,
,
∴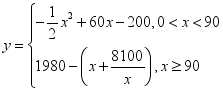 ,
,
(2)当![]() 时,
时,![]() ,
,
∴当![]() 时,
时,![]() 取最大值,最大值为1600万元;
取最大值,最大值为1600万元;
当![]() 时,
时,![]() ,
,
当且仅当![]() ,即
,即![]() 时,
时,![]() 取得最大值,最大值为1800万元.
取得最大值,最大值为1800万元.
综上,当产量为90万箱时,该口罩生产厂在生产中获得利润最大,最大利润为1800万元.
22.【详解】(1)由![]() 得:
得:![]()
由切线方程可知:![]()
![]() ,
,![]() ,解得:
,解得:![]() ,
,![]()
(2)由(1)知![]()
则![]() 时,
时,![]() 恒成立等价于
恒成立等价于![]() 时,
时,![]() 恒成立
恒成立
令![]() ,
,![]() ,则
,则![]()
令![]() ,则
,则![]()
![]() 当
当![]() 时,
时,![]() ,则
,则![]() 单调递增
单调递增
![]() ,
,![]()
![]() ,使得
,使得![]()
当![]() 时,
时,![]() ;
;![]() 时,
时,![]()
![]()
![]()
![]()
![]()
![]() ,即正整数
,即正整数![]() 的最大值为
的最大值为![]()
2024南充高三上学期高考适应性考试(一诊)数学(文)含答案: 这是一份2024南充高三上学期高考适应性考试(一诊)数学(文)含答案,文件包含四川省南充市2024届高三高考适应性考试一诊考试数学文试题docx、四川省南充市2024届高三高考适应性考试一诊考试数学文答案pdf等2份试卷配套教学资源,其中试卷共15页, 欢迎下载使用。
江苏省徐州市大许中学2021届高三上学期期中适应性考试数学试卷 Word版含答案: 这是一份江苏省徐州市大许中学2021届高三上学期期中适应性考试数学试卷 Word版含答案,共10页。试卷主要包含了已知为虚数单位,复数满足,则=,设函数,如果,则的值是,下列指定的函数中,一定有的有等内容,欢迎下载使用。
2021届高三上学期第三次考试数学(文)试卷 Word版含答案: 这是一份2021届高三上学期第三次考试数学(文)试卷 Word版含答案,共11页。













