高考数学一轮复习检测：第3章第5节 正弦定理和余弦定理 含解析

这是一份高考数学一轮复习检测：第3章第5节 正弦定理和余弦定理 含解析，共10页。
限时规范训练(限时练·夯基练·提能练)A级　基础夯实练1．(2018·广东广州调研)△ABC的内角A，B，C所对的边分别为a，b，c，已知b＝，c＝4，cos B＝，则△ABC的面积为(　　)A．3　　　　　　　 B．C．9  D．解析：选B.由余弦定理b2＝c2＋a2－2accos B，得7＝16＋a2－6a，解得a＝3，∵cos B＝，∴sin B＝，∴S△ABC＝casin B＝×4×3×＝.故选B.2．(2018·河南三市联考)已知a，b，c分别为△ABC三个内角A，B，C的对边，sin A∶sin B＝1∶，c＝2cos C＝，则△ABC的周长为(　　)A．3＋3  B．2C．3＋2  D．3＋解析：选C.因为sin A∶sin B＝1∶，所以b＝a，由余弦定理得cos C＝＝＝，又c＝，所以a＝，b＝3，所以△ABC的周长为3＋2，故选C.3．(2018·成都外国语学校二模)在△ABC中，sin2A≤sin2B＋sin2C－sin Bsin C，则A的取值范围是(　　)A.  B．C.  D．解析：选C.由正弦定理及sin2A≤sin2B＋sin2C－sin Bsin C可得a2≤b2＋c2－bc，即b2＋c2－a2≥bc，由余弦定理可得cos A＝≥＝，又0＜A＜π，所以0＜A≤.故A的取值范围是.故选C.4．(2017·山东卷)在△ABC中，角A，B，C的对边分别为a，b，c.若△ABC为锐角三角形，且满足sin B(1＋2cos C)＝2sin Acos C＋cos Asin C，则下列等式成立的是(　　)A．a＝2b  B．b＝2aC．A＝2B  D．B＝2A解析：选A.因为A＋B＋C＝π，sin B(1＋2cos C)＝2sin Acos C＋cos Asin C，所以sin(A＋C)＋2sin Bcos C＝2sin Acos C＋cos Asin C，所以2sin B cos C＝sin Acos C.又cos C≠0，所以2sin B＝sin A，所以2b＝a，故选A.5．(2018·东北三校联考)已知△ABC的内角A，B，C的对边分别为a，b，c，且＝，则B等于(　　)A.  B．C.  D．解析：选C.根据正弦定理＝＝＝2R，得＝＝，即a2＋c2－b2＝ac，得cos B＝＝，又0＜B＜π，所以B＝，故选C.6．(2018·长沙模拟)在△ABC中，A＝，b2sin C＝4sin B，则△ABC的面积为________．解析：因为b2sin C＝4sin B，所以b2c＝4b，即bc＝4，故S△ABC＝bcsin A＝×4×＝2.答案：27．(2018·山西大同联考)在△ABC中，角A，B，C的对边分别为a，b，c，若2(bcos A＋acos B)＝c2，b＝3，3cos A＝1，则a的值为________．解析：由正弦定理可得2(sin Bcos A＋sin Acos B)＝csin C，∵2(sin Bcos A＋sin Acos B)＝2sin(A＋B)＝2sin C，∴2sin C＝csin C，∵sin C＞0，∴c＝2，由余弦定理得a2＝b2＋c2－2bccos A＝22＋32－2×2×3×＝9，∴a＝3.答案：38．(2018·辽宁沈阳模拟)在△ABC中，内角A，B，C的对边分别为a，b，c，已知c＝5，B＝，△ABC的面积为，则cos 2A＝________．解析：由三角形的面积公式，得S△ABC＝acsin B＝×a×5×sin＝××5a＝，解得a＝3.由b2＝a2＋c2－2accos B＝32＋52－2×3×5×＝49，得b＝7.由＝⇒sin A＝sin B＝sin ＝，∴cos 2A＝1－2sin2A＝1－2×＝.答案：9．(2017·全国卷Ⅰ)△ABC的内角A，B，C的对边分别为a，b，c.已知△ABC的面积为.(1)求sin Bsin C；(2)若6cos Bcos C＝1，a＝3，求△ABC的周长．解：(1)由题设得acsin B＝，即csin B＝.由正弦定理得sin Csin B＝.故sin Bsin C＝.(2)由题设及(1)得cos Bcos C－sin Bsin C＝－，即cos(B＋C)＝－.所以B＋C＝，故A＝.由题设得bcsin A＝，a＝3，即bc＝8.由余弦定理得b2＋c2－bc＝9，即(b＋c)2－3bc＝9，由bc＝8，得b＋c＝.故△ABC的周长为3＋.10．在△ABC中，角A，B，C所对的边分别是a，b，c，且＋＝.(1)证明：sin Asin B＝sin C.(2)若b2＋c2－a2＝bc，求tan B．解：(1)证明：由正弦定理＝＝，可知原式可以化简为＋＝＝1，因为A和B为三角形的内角，所以sin Asin B≠0，则两边同时乘以sin Asin B，可得sin Bcos A＋sin Acos B＝sin Asin B，由和角公式可知，sin Bcos A＋sin Acos B＝sin(A＋B)＝sin(π－C)＝sin C，∴sin C＝sin Asin B，故原式得证．(2)由b2＋c2－a2＝bc，根据余弦定理可知，cos A＝＝.因为A为三角形内角，A∈(0，π)，sin A＞0，则sin A＝＝，即＝，由(1)可知＋＝＝1，所以＝＝1－＝1－＝，所以tan B＝4.B级　能力提升练11．在△ABC中，B＝，BC边上的高等于BC，则cos A＝(　　)A.  B．C．－  D．－解析：选C.如图，过A作AD⊥BC，垂足为D，由题意知AD＝BD＝BC，则CD＝BC，AB＝BC，AC＝BC，在△ABC中，由余弦定理的推论可知，cos∠BAC＝＝＝－，故选C. 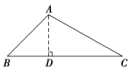12．(2018·六安模拟)在△ABC中，角A，B，C的对边分别为a，b，c，若cos A＋sin A－＝0，则的值是(　　)A．1  B．C.  D．2解析：选B.因为cos A＋sin A－＝0，所以(cos A＋sin A)(cos B＋sin B)＝2，所以cos Acos B＋sin Asin B＋sin Acos B＋cos Asin B＝2，即cos(A－B)＋sin(A＋B)＝2，所以cos(A－B)＝1，sin(A＋B)＝1，又A，B分别为三角形的内角，所以A＝B，A＋B＝，所以a＝b，C＝，所以＝＝，故选B.13．(2017·浙江卷)已知△ABC中，AB＝AC＝4，BC＝2.点D为AB延长线上一点，BD＝2，连接CD，则△BDC的面积是________，cos∠BDC＝________．解析：由余弦定理得cos∠ABC＝＝，∴cos∠CBD＝－，sin∠CBD＝，∴S△BDC＝BD·BC·sin∠CBD＝×2×2×＝.又cos∠ABC＝cos 2∠BDC＝2cos2∠BDC－1＝，0＜∠BDC＜，∴cos∠BDC＝.答案：；14．在锐角三角形ABC中，a，b，c分别为角A，B，C的对边，且4sin Acos2A－cos(B＋C)＝sin 3A＋.(1)求A的大小；(2)若b＝2，求△ABC面积的取值范围．解：(1)∵A＋B＋C＝π，∴cos(B＋C)＝－cos A①，∵3A＝2A＋A，∴sin 3A＝sin(2A＋A)＝sin 2Acos A＋cos 2Asin A②，又sin 2A＝2sin Acos A③，将①②③代入已知，得2sin 2Acos A＋cos A＝sin 2Acos A＋cos 2Asin A＋，整理得sin A＋cos A＝，即sin＝，又A∈，∴A＋＝，即A＝.(2)由(1)得B＋C＝，∴C＝－B，∵△ABC为锐角三角形，∴－B∈且B∈，解得B∈，在△ABC中，由正弦定理得＝，∴c＝＝＝＋1，又B∈，∴∈(0，)，∴c∈(1，4)，∵S△ABC＝bcsin A＝c，∴S△ABC∈.15．在△ABC中，角A，B，C的对边分别为a，b，c.已知2(tan A＋tan B)＝＋.(1)证明：a＋b＝2c；(2)求cos C的最小值．解：(1)由题意知2＝＋，化简得2(sin Acos B＋sin Bcos A)＝sin A＋sin B，即2sin(A＋B)＝sin A＋sin B．因为A＋B＋C＝π，所以sin(A＋B)＝sin(π－C)＝sin C.从而sin A＋sin B＝2sin C.由正弦定理得a＋b＝2c.(2)由(1)知c＝，所以cos C＝＝＝－≥，当且仅当a＝b时，等号成立．故cos C的最小值为.C级　素养加强练16．(2018·湖北八校联考)在△ABC中，角A，B，C的对边分别为a，b，c.(1)若23cos2 A＋cos 2A＝0，且△ABC为锐角三角形，a＝7，c＝6，求b的值；(2)若a＝，A＝，求b＋c的取值范围．解：(1)∵23cos2 A＋cos 2A＝23cos2 A＋2cos2 A－1＝0，∴cos2 A＝，又A为锐角，∴cos A＝，而a2＝b2＋c2－2bccos A，即b2－b－13＝0，解得b＝5(负值舍去)，∴b＝5.(2)解法一：由正弦定理可得b＋c＝2(sin B＋sin C)＝2＝2sin，∵0＜B＜，∴＜B＋＜，∴＜sin≤1，∴b＋c∈(，2]．解法二：由余弦定理a2＝b2＋c2－2bccos A可得b2＋c2－3＝bc，即(b＋c)2－3＝3bc≤(b＋c)2，当且仅当b＝c时取等号，∴b＋c≤2，又由两边之和大于第三边可得b＋c＞，∴b＋c的取值范围为(，2]．