


所属成套资源:高考数学一轮复习 精选习题 含解析
高考数学一轮复习 精选习题:第三篇 三角函数、解三角形 第4节 三角函数的图象与性质 Word版含解析
展开
这是一份高考数学一轮复习 精选习题:第三篇 三角函数、解三角形 第4节 三角函数的图象与性质 Word版含解析,共9页。

 www.ks5u.com第4节 三角函数的图象与性质
www.ks5u.com第4节 三角函数的图象与性质![]() 【选题明细表】知识点、方法题号三角函数的定义域、值域与最值1,7三角函数的单调性、单调区间3,9,13三角函数的奇偶性、周期性与对称性2,5,6,8,10综合应用4,11,12,14基础巩固(时间:30分钟)1.函数y=
【选题明细表】知识点、方法题号三角函数的定义域、值域与最值1,7三角函数的单调性、单调区间3,9,13三角函数的奇偶性、周期性与对称性2,5,6,8,10综合应用4,11,12,14基础巩固(时间:30分钟)1.函数y=![]() 的定义域为( C )(A)[-
的定义域为( C )(A)[-![]() ,
,![]() ](B)[kπ-
](B)[kπ-![]() ,kπ+
,kπ+![]() ](k∈Z)(C)[2kπ-
](k∈Z)(C)[2kπ-![]() ,2kπ+
,2kπ+![]() ](k∈Z)(D)R解析:因为cos x-
](k∈Z)(D)R解析:因为cos x-![]() ≥0,得cos x≥
≥0,得cos x≥![]() ,所以2kπ-
,所以2kπ-![]() ≤x≤2kπ+
≤x≤2kπ+![]() ,k∈Z.2.(2018·全国Ⅲ卷)函数f(x)=
,k∈Z.2.(2018·全国Ⅲ卷)函数f(x)=![]() 的最小正周期为( C )(A)
的最小正周期为( C )(A)![]() (B)
(B)![]() (C)π (D)2π解析:由已知得f(x)=
(C)π (D)2π解析:由已知得f(x)=![]() =
=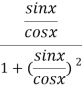 =
=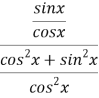 =sin x·cos x=
=sin x·cos x=![]() sin 2x,所以f(x)的最小正周期为T=
sin 2x,所以f(x)的最小正周期为T=![]() =π.故选C.3.函数y=2sin(
=π.故选C.3.函数y=2sin(![]() -2x)(x∈[0,π])的一个递增区间是( A )(A)[
-2x)(x∈[0,π])的一个递增区间是( A )(A)[![]() ,
,![]() ] (B)[
] (B)[![]() ,π](C)[
,π](C)[![]() ,
,![]() ] (D)[-
] (D)[-![]() ,
,![]() ]解析:首先将函数化为y=-2sin(2x-
]解析:首先将函数化为y=-2sin(2x-![]() )(x∈[0,π]),令t=2x-
)(x∈[0,π]),令t=2x-![]() ,x增大,t增大,所以为求函数的增区间,需研究y=2sin t的减区间.由
,x增大,t增大,所以为求函数的增区间,需研究y=2sin t的减区间.由![]() +2kπ≤2x-
+2kπ≤2x-![]() ≤
≤![]() +2kπ,k∈Z得
+2kπ,k∈Z得![]() +kπ≤x≤
+kπ≤x≤![]() +kπ,k∈Z,所以k=0时得[
+kπ,k∈Z,所以k=0时得[![]() ,
,![]() ],故选A.4.(2018·全国Ⅰ卷)已知函数f(x)=2cos2x-sin2x+2,则( B )(A)f(x)的最小正周期为π,最大值为3(B)f(x)的最小正周期为π,最大值为4(C)f(x)的最小正周期为2π,最大值为3(D)f(x)的最小正周期为2π,最大值为4解析:因为f(x)=2cos2x-sin2x+2=1+cos 2x-
],故选A.4.(2018·全国Ⅰ卷)已知函数f(x)=2cos2x-sin2x+2,则( B )(A)f(x)的最小正周期为π,最大值为3(B)f(x)的最小正周期为π,最大值为4(C)f(x)的最小正周期为2π,最大值为3(D)f(x)的最小正周期为2π,最大值为4解析:因为f(x)=2cos2x-sin2x+2=1+cos 2x-![]() +2=
+2=![]() cos 2x+
cos 2x+![]() ,所以f(x)的最小正周期为π,最大值为4.故选B.5.将函数y=2sin(x+
,所以f(x)的最小正周期为π,最大值为4.故选B.5.将函数y=2sin(x+![]() )cos(x+
)cos(x+![]() )的图象向左平移
)的图象向左平移![]() (
(![]() >0)个单位长度,所得图象对应的函数恰为奇函数,则
>0)个单位长度,所得图象对应的函数恰为奇函数,则![]() 的最小值为( B )(A)
的最小值为( B )(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]() 解析:根据题意可得y=sin(2x+
解析:根据题意可得y=sin(2x+![]() ),将其图象向左平移
),将其图象向左平移![]() (
(![]() >0)个单位长度,可得y=sin(2x+
>0)个单位长度,可得y=sin(2x+![]() +2
+2![]() )的图象.因为该图象所对应的函数恰为奇函数,所以
)的图象.因为该图象所对应的函数恰为奇函数,所以![]() +2
+2![]() =kπ(k∈Z),
=kπ(k∈Z),![]() =
=![]() -
-![]() (k∈Z),又
(k∈Z),又![]() >0,所以当k=1时,
>0,所以当k=1时,![]() 取得最小值,且
取得最小值,且![]() min=
min=![]() ,故选B. 6.已知函数f(x)=2sin(
,故选B. 6.已知函数f(x)=2sin(![]() x+
x+![]() ),若对任意的实数x,总有f(x1)≤f(x)≤f(x2),则|x1-x2|的最小值是( A )(A)2 (B)4 (C)π (D)2π解析:由题意可得|x1-x2|的最小值为半个周期,即
),若对任意的实数x,总有f(x1)≤f(x)≤f(x2),则|x1-x2|的最小值是( A )(A)2 (B)4 (C)π (D)2π解析:由题意可得|x1-x2|的最小值为半个周期,即![]() =
=![]() =2.故选A.7.(2017·全国Ⅱ卷)函数f(x)=2cos x+sin x的最大值为 . 解析:f(x)=2cos x+sin x=
=2.故选A.7.(2017·全国Ⅱ卷)函数f(x)=2cos x+sin x的最大值为 . 解析:f(x)=2cos x+sin x=![]() (
(![]() cos x+
cos x+![]() sin x)=
sin x)=![]() sin (x+θ),其中tan θ=2,所以f(x)的最大值为
sin (x+θ),其中tan θ=2,所以f(x)的最大值为![]() .答案:
.答案:![]() 8.已知点P(4,-3)在角
8.已知点P(4,-3)在角![]() 的终边上,函数f(x)=sin(ωx+
的终边上,函数f(x)=sin(ωx+![]() )(ω>0)图象上与y轴最近的两个对称中心间的距离为
)(ω>0)图象上与y轴最近的两个对称中心间的距离为![]() ,则f(
,则f(![]() )的值为 . 解析:由题意
)的值为 . 解析:由题意![]() =
=![]() ,则T=π,即ω=
,则T=π,即ω=![]() =2,则f(x)=sin(2x+
=2,则f(x)=sin(2x+![]() );又由三角函数的定义可得sin
);又由三角函数的定义可得sin ![]() =-
=-![]() ,cos
,cos ![]() =
=![]() ,则f(
,则f(![]() )=sin
)=sin![]() cos
cos ![]() +cos
+cos![]() sin
sin ![]() =
=![]() .答案:
.答案:![]() 能力提升(时间:15分钟)9.(2018·大连二十四中模拟)已知f(x)是偶函数,当x∈[0,
能力提升(时间:15分钟)9.(2018·大连二十四中模拟)已知f(x)是偶函数,当x∈[0,![]() ]时,f(x)=xsin x.若a=f(cos 1),b=f(cos 2),c=f(cos 3),则a,b,c的大小关系为( B )(A)a<b<c (B)b<a<c(C)c<b<a (D)b<c<a解析:由于函数f(x)为偶函数,故b=f(cos 2)=f(-cos 2),c=f(cos 3)=f(-cos 3).由于x∈[0,
]时,f(x)=xsin x.若a=f(cos 1),b=f(cos 2),c=f(cos 3),则a,b,c的大小关系为( B )(A)a<b<c (B)b<a<c(C)c<b<a (D)b<c<a解析:由于函数f(x)为偶函数,故b=f(cos 2)=f(-cos 2),c=f(cos 3)=f(-cos 3).由于x∈[0,![]() ],f′(x)=sin x+xcos x≥0,所以函数在区间[0,
],f′(x)=sin x+xcos x≥0,所以函数在区间[0,![]() ]上为增函数.因为0<-cos 2<cos 1<-cos 3<
]上为增函数.因为0<-cos 2<cos 1<-cos 3<![]() ,根据函数单调性可得f(-cos 2)<f(cos 1)<f(-cos 3),故b<a<c.10.(2018·绵阳一诊)已知函数f(x)=sin ωx+
,根据函数单调性可得f(-cos 2)<f(cos 1)<f(-cos 3),故b<a<c.10.(2018·绵阳一诊)已知函数f(x)=sin ωx+![]() cos ωx(ω>0)图象的最高点与相邻最低点的距离是
cos ωx(ω>0)图象的最高点与相邻最低点的距离是![]() ,若将y=f(x)的图象向右平移
,若将y=f(x)的图象向右平移![]() 个单位得到y=g(x)的图象,则函数y=g(x)图象的一条对称轴方程是( B )(A)x=
个单位得到y=g(x)的图象,则函数y=g(x)图象的一条对称轴方程是( B )(A)x=![]() (B)x=
(B)x=![]() (C)x=
(C)x=![]() (D)x=0解析:f(x)=sin ωx+
(D)x=0解析:f(x)=sin ωx+![]() cos ωx=2sin(ωx+
cos ωx=2sin(ωx+![]() ),ω>0.设函数f(x)的周期为T.则由题意得(
),ω>0.设函数f(x)的周期为T.则由题意得(![]() )2+[2-(-2)]2=(
)2+[2-(-2)]2=(![]() )2,得T=2.所以
)2,得T=2.所以![]() =2,所以ω=π.则f(x)=2sin(πx+
=2,所以ω=π.则f(x)=2sin(πx+![]() ).y=g(x)=2sin[π(x-
).y=g(x)=2sin[π(x-![]() )+
)+![]() ]=2sin(πx+
]=2sin(πx+![]() ).令πx+
).令πx+![]() =
=![]() +kπ,k∈Z得x=k+
+kπ,k∈Z得x=k+![]() ,k∈Z.当k=0时,函数y=g(x)图象的一条对称轴方程为x=
,k∈Z.当k=0时,函数y=g(x)图象的一条对称轴方程为x=![]() .故选B.11.(2018·重庆巴蜀中学模拟)已知函数f(x)=2
.故选B.11.(2018·重庆巴蜀中学模拟)已知函数f(x)=2![]() cos x·sin x+2sin2x(x∈R),给出下列五个命题:①(
cos x·sin x+2sin2x(x∈R),给出下列五个命题:①(![]() ,0)是函数f(x)图象的一个对称中心;②f(x)的最小正周期是2π;③f(x)在区间[-
,0)是函数f(x)图象的一个对称中心;②f(x)的最小正周期是2π;③f(x)在区间[-![]() ,
,![]() ]上是增函数;④f(x)的图象关于直线x=
]上是增函数;④f(x)的图象关于直线x=![]() 对称;⑤x∈[-
对称;⑤x∈[-![]() ,
,![]() ]时,f(x)的值域为[1-
]时,f(x)的值域为[1-![]() ,3].其中正确的命题为( D )(A)①②④ (B)③④⑤(C)②③ (D)③④解析:将原函数化简得,f(x)=
,3].其中正确的命题为( D )(A)①②④ (B)③④⑤(C)②③ (D)③④解析:将原函数化简得,f(x)=![]() sin 2x-cos 2x+1=2sin(2x-
sin 2x-cos 2x+1=2sin(2x-![]() )+1(x∈R),其对称中心为(
)+1(x∈R),其对称中心为(![]() +
+![]() ,1)(k∈Z),故①错;最小正周期T=
,1)(k∈Z),故①错;最小正周期T=![]() =π,故②错;f(x)在-
=π,故②错;f(x)在-![]() +2kπ≤2x-
+2kπ≤2x-![]() ≤
≤![]() +2kπ,k∈Z,即-
+2kπ,k∈Z,即-![]() +kπ≤x≤
+kπ≤x≤![]() +kπ,k∈Z上单调递增,所以当k=0时,f(x)在[-
+kπ,k∈Z上单调递增,所以当k=0时,f(x)在[-![]() ,
,![]() ]上是增函数,故③正确;令2x-
]上是增函数,故③正确;令2x-![]() =
=![]() +kπ,k∈Z,则对称轴为x=
+kπ,k∈Z,则对称轴为x=![]() +
+![]() ,k∈Z,所以当k=0时,x=
,k∈Z,所以当k=0时,x=![]() 是其对称轴,故④正确;因为函数在[-
是其对称轴,故④正确;因为函数在[-![]() ,-
,-![]() ]上单调递减,在[-
]上单调递减,在[-![]() ,
,![]() ]上单调递增,故其最小值为f(-
]上单调递增,故其最小值为f(-![]() )=-1,最大值为f(
)=-1,最大值为f(![]() )=3,故当x∈[-
)=3,故当x∈[-![]() ,
,![]() ]时,f(x)的值域为[-1,3],故⑤错.12.(2018·山西运城康杰中学一模)已知x1,x2是函数f(x)=2sin 2x+cos 2x-m在[0,
]时,f(x)的值域为[-1,3],故⑤错.12.(2018·山西运城康杰中学一模)已知x1,x2是函数f(x)=2sin 2x+cos 2x-m在[0,![]() ]内的两个零点,则sin(x1+x2)= . 解析:f(x)=2sin 2x+cos 2x-m=
]内的两个零点,则sin(x1+x2)= . 解析:f(x)=2sin 2x+cos 2x-m=![]() sin(2x+
sin(2x+![]() )-m,其中 (cos
)-m,其中 (cos ![]() =
=![]() ,sin
,sin ![]() =
=![]() ),由函数f(x)在[0,
),由函数f(x)在[0,![]() ]内的两个零点,知方程
]内的两个零点,知方程![]() sin(2x+
sin(2x+![]() )-m=0在[0,
)-m=0在[0,![]() ]内有两个根,即函数y=m与y=
]内有两个根,即函数y=m与y=![]() sin(2x+
sin(2x+![]() )的图象在[0,
)的图象在[0,![]() ]内有两个交点,且x1,x2关于直线x=
]内有两个交点,且x1,x2关于直线x=![]() -
-![]() 对称,所以x1+x2=
对称,所以x1+x2=![]() -
-![]() ,所以sin(x1+x2)=sin(
,所以sin(x1+x2)=sin(![]() -
-![]() )=cos
)=cos ![]() =
=![]() .答案:
.答案:![]() 13.已知函数f(x)=-2sin(2x+
13.已知函数f(x)=-2sin(2x+![]() )(|
)(|![]() |<π),若(
|<π),若(![]() ,
,![]() )是f(x)的一个单调递增区间,则
)是f(x)的一个单调递增区间,则![]() 的值为 . 解析:令
的值为 . 解析:令![]() +2kπ≤2x+
+2kπ≤2x+![]() ≤
≤![]() +2kπ,k∈Z,有
+2kπ,k∈Z,有![]() -
-![]() +kπ≤x≤
+kπ≤x≤![]() -
-![]() +kπ,k∈Z,此时函数单调递增,若(
+kπ,k∈Z,此时函数单调递增,若(![]() ,
,![]() )是f(x)的一个单调递增区间,则必有
)是f(x)的一个单调递增区间,则必有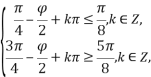 解得
解得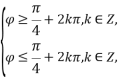 故
故![]() =
=![]() +2kπ,k∈Z,又|
+2kπ,k∈Z,又|![]() |<π,所以
|<π,所以![]() =
=![]() .答案:
.答案:![]() 14.(2018·长沙一中模拟)设函数f(x)=Asin (ωx+
14.(2018·长沙一中模拟)设函数f(x)=Asin (ωx+![]() )(A,ω,
)(A,ω,![]() 是常数,A>0,ω>0).若f(x)在区间[
是常数,A>0,ω>0).若f(x)在区间[![]() ,
,![]() ]上具有单调性,且f(
]上具有单调性,且f(![]() )=f(
)=f(![]() )=-f(
)=-f(![]() ),则f(x)的最小正周期为 . 解析:因为f(x)在[
),则f(x)的最小正周期为 . 解析:因为f(x)在[![]() ,
,![]() ]上具有单调性,且f(
]上具有单调性,且f(![]() )=f(
)=f(![]() )=-f(
)=-f(![]() ),则
),则![]() ×
×![]() ≥
≥![]() -
-![]() ,且函数的图象关于直线x=
,且函数的图象关于直线x=![]() =
=![]() 对称,且一个对称点为(
对称,且一个对称点为(![]() ,0),可得0<ω≤3.且
,0),可得0<ω≤3.且![]() -
-![]() =
=![]() ×
×![]() ,得ω=2.所以f(x)的最小正周期T=
,得ω=2.所以f(x)的最小正周期T=![]() =π.答案:π
=π.答案:π
相关试卷
这是一份新高考数学一轮复习精选讲练专题4.8 三角函数的图象与性质(含解析),共18页。
这是一份新高考数学一轮复习精选讲练专题4.7 三角函数的图象与性质(含解析),共19页。试卷主要包含了正弦函数与余弦函数的图象,正弦函数与余弦函数的性质,正切函数的性质与图象,余切函数的图象及性质等内容,欢迎下载使用。
这是一份新高考数学一轮复习课时过关练习第04章 三角函数、解三角形第4节 三角函数的图象与性质 (含解析),共22页。试卷主要包含了能画出三角函数的图象等内容,欢迎下载使用。









