冀教版八年级上册12.4 分式方程同步练习题

这是一份冀教版八年级上册12.4 分式方程同步练习题，共7页。试卷主要包含了4 分式方程》课时练习，下列方程不是分式方程的是等内容，欢迎下载使用。
2023年冀教版数学八年级上册《12.4 分式方程》课时练习一              、选择题1.下列方程不是分式方程的是(　　)A.＝1         B.﹣＝      C.＝         D.﹣＝72.当x，y满足什么条件时，分式有意义?(     )A.x，y不都为0      B.x，y都不为0      C.x，y都为0        D.x＝﹣y3.若关于x的分式方程的解为x=2，则m值为(　　)A.2         B.0            C.6           D.44.解分式方程﹣2＝，去分母得(     )A.1﹣2(x﹣5)＝﹣3        B.1﹣2(x﹣5)＝3C.1﹣2x﹣10＝﹣3         D.1﹣2x＋10＝35.分式方程－1＝的解为(　　)A.x＝1         B.x＝2         C.x＝－1                            D.无解6.如图，在下框解分式方程的4个步骤中，根据等式基本性质的是(　　)A.①②         B.②④         C.①③         D.③④7.解分式方程＋=分以下几步，其中错误的一步是(  )A.方程两边分式的最简公分母是(x－1)(x＋1)B.方程两边都乘以(x－1)(x＋1)，得整式方程2(x－1)＋3(x＋1)=6C.解这个整式方程，得x=1D.原方程的解为x=18.已知关于x的分式方程＋2＝﹣的解为非负数，则正整数m的所有个数为(　　)A.3        B.4        C.5        D.6二              、填空题9.若关于x的方程的解为x=4，则m=   .10.方程＝的解为          .11.若关于x的分式方程无解，则m的值为       .12.如果，则m=_______.13.已知分式方程，如果设，那么原方程可化为关于y的整式方程是    .14.定义运算“※”：a※b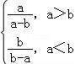＝，若5※x＝2，则x的值为　   　.三              、解答题15.解分式方程：﹣＝1；     16.解分式方程：＝；    17.解分式方程：－＝1；　    18.解方程：＋ = .     19.若关于x的分式方程=－2的解为非负数，求a的取值范围.      20.以下是小明同学解分式方程=－2的过程.解：方程两边同时乘(x－3)，得1－x=－1－2.　　…………………………第一步解得x=4.　……………………………………第二步检验：当x=4时，x－3=4－3=1≠0.　 ………第三步所以，原分式方程的解为x=4.…………………第四步(1)小明的解法从第________步开始出现错误；(2)写出解分式方程=－2的正确过程.        21.解分式方程：＋＋＝.          22.观察下列方程的特征及其解的特点.①x＋=－3的解为x1=－1，x2=－2；②x＋=－5的解为x1=－2，x2=－3；③x＋=－7的解为x1=－3，x2=－4.解答下列问题：(1)请你写出一个符合上述特征的方程：___________，其解为____________；(2)根据这类方程特征，写出第n个方程：__________________，其解为______________；(3)请利用(2)的结论，求关于x的方程x＋=－2(n＋2)(其中n为正整数)的解.
参考答案1.B2.A.3.C4.A5.D6.C7.D8.B.9.答案为：3；10.答案为：x＝3.11.答案为：±.12.答案为：-5.13.答案为：y2-3y+2=0； 14.答案为：或10.15.解：去分母得x2﹣2x＋2＝x2﹣x，解得x＝2，检验：当x＝2时，x(x﹣1)≠0，故x＝2是原方程的解；16.解：方程两边同乘以(x＋2)(x﹣2)，得4(x＋2)＝x﹣2，解得x＝﹣，检验：将 x＝﹣代入(x＋2)(x﹣2)中，(x＋2)(x﹣2)≠0，∴x＝﹣是原分式方程的解.故原分式方程的解为 x＝﹣；17.解：方程两边同乘(x＋3)(x－3)，得(x－2)(x－3)－3(x＋3)＝(x＋3)(x－3)，整理得－8x＝－6，解得x＝.经检验，x＝是原方程的根.18.解：方程两边都乘以(x＋2)(x－2)，得x＋2(x－2)=x＋2.解得x=3.经检验，x=3是原方程的解.19.解：方程两边同时乘2x－2，得2x=3a－2(2x－2)，整理得6x=3a＋4，∴x=.∵方程的解为非负数，∴≥0，解得a≥－.又∵x≠1，∴≠1，∴a≠.故a的取值范围是a≥－且a≠.20.解：(1)一(2)方程两边同时乘(x－3)，得1－x=－1－2x＋6，解得x=4.检验：当x=4时，x－3≠0.所以，原分式方程的解为x=4.21.解：原方程变形为(－)＋(－)＋(－)＝.整理，得－＝，去分母，得2(x＋9)－2x＝9x，解得x＝2.经检验，x＝2是原分式方程的解.22.解：(1)x＋=－9　x1=－4，x2=－5(2)x＋=－(2n＋1)　x1=－n，x2=－n－1(3)x＋=－2(n＋2)，x＋3＋=－2(n＋2)＋3，(x＋3)＋=－(2n＋1)，由(2)知x＋3=－n或x＋3=－(n＋1)，即x1=－n－3，x2=－n－4.检验：∵n为正整数，当x1=－n－3时，x＋3=－n≠0；当x2=－n－4时，x＋3=－n－1≠0.∴原分式方程的解是x1=－n－3，x2=－n－4.