

所属成套资源:高考数学二轮复习题海集训 (30题含答案)
高考数学二轮复习题海集训04 指数函数(30题含答案)
展开
这是一份高考数学二轮复习题海集训04 指数函数(30题含答案),共5页。试卷主要包含了5 C,72等内容,欢迎下载使用。
2020高考数学(理数)题海集训04 指数函数一 、选择题1.下列命题中正确的个数为( )①-3是81的四次方根; ②正数的n次方根有两个; ③a的n次方根就是![]() ; ④
; ④![]() =a(a≥0)A.1个 B.2个 C.3个 D.4个 2.下列结论中正确的个数是( )①当a<0时,
=a(a≥0)A.1个 B.2个 C.3个 D.4个 2.下列结论中正确的个数是( )①当a<0时,![]() =a3; ②
=a3; ②![]() =|a|;③函数y=
=|a|;③函数y=![]() -(3x-7)0的定义域是(2,+∞); ④若100a=5,10b=2,则2a+b=1A.0 B.1 C.2 D.3 3.若
-(3x-7)0的定义域是(2,+∞); ④若100a=5,10b=2,则2a+b=1A.0 B.1 C.2 D.3 3.若![]() ,则实数a的取值范围是( ) A.a∈R B.a=0.5 C.a>0.5 D.a≤0.54.函数
,则实数a的取值范围是( ) A.a∈R B.a=0.5 C.a>0.5 D.a≤0.54.函数 ,满足
,满足![]() 的
的![]() 的取值范围 ( )A.
的取值范围 ( )A.![]() B.
B. ![]() C.
C.![]() D.
D.![]() 5.函数
5.函数![]() ( )A.
( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 6.若指数函数
6.若指数函数![]() 在[-1,1]上的最大值与最小值的差是1,则底数a等于 ( )A.
在[-1,1]上的最大值与最小值的差是1,则底数a等于 ( )A.![]() B.
B. ![]() C.
C.![]() D.
D. ![]() 7.函数y=5-|x|的图象是( )
7.函数y=5-|x|的图象是( ) 8.函数y=a|x|(a>1)的图象是( )
8.函数y=a|x|(a>1)的图象是( )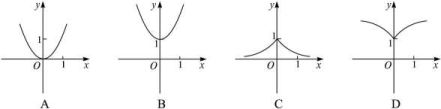 9.若m<0,n>0,则
9.若m<0,n>0,则![]() 等于( )A.
等于( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 10.计算
10.计算![]() 的结果是( )A.a16 B.a8 C.a4 D.a2 11.函数f(x)=(a-1)x在R上是减函数,则a的取值范围( )A、0<a<1 B、1<a<2 C、a>1 D、a>212.函数y=(a2-3a+3)ax是指数函数,则有( )A.a=1或a=2 B.a=1 C.a=2 D.a>0,且a≠1 13.设a=
的结果是( )A.a16 B.a8 C.a4 D.a2 11.函数f(x)=(a-1)x在R上是减函数,则a的取值范围( )A、0<a<1 B、1<a<2 C、a>1 D、a>212.函数y=(a2-3a+3)ax是指数函数,则有( )A.a=1或a=2 B.a=1 C.a=2 D.a>0,且a≠1 13.设a=![]() ,b=
,b=![]() ,c=
,c=![]() ,则a、b、c的大小关系是( ) A.a>c>b B.a>b>c C.c>a>b D.b>c>a14.已知函数f(x)=ax,其中a>0,且a≠1,如果以P(x1,f(x1)),Q(x2,f(x2))为端点的线段的中点在y轴上,那么f(x1)·f(x2)等于( )A.1 B.a C.2 D.a2 15.已知0<a<1,b<-1,则函数y=ax+b的图象不经过( )
,则a、b、c的大小关系是( ) A.a>c>b B.a>b>c C.c>a>b D.b>c>a14.已知函数f(x)=ax,其中a>0,且a≠1,如果以P(x1,f(x1)),Q(x2,f(x2))为端点的线段的中点在y轴上,那么f(x1)·f(x2)等于( )A.1 B.a C.2 D.a2 15.已知0<a<1,b<-1,则函数y=ax+b的图象不经过( )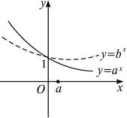 A.第一象限 B.第二象限 C.第三象限 D.第四象限 16.函数在区间上的单调性是( )A、 增函数 B、 减函数C、 常数 D、 有时是增函数有时是减函数 17.函数y=ax+b(a>0且a≠1)与y=ax+b的图象有可能是( ) .
A.第一象限 B.第二象限 C.第三象限 D.第四象限 16.函数在区间上的单调性是( )A、 增函数 B、 减函数C、 常数 D、 有时是增函数有时是减函数 17.函数y=ax+b(a>0且a≠1)与y=ax+b的图象有可能是( ) .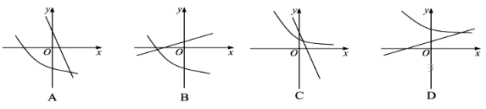 18.函数f(x)=a|x+1|(a>0,且a≠1)的值域为[1,+∞),则f(-4)与f(1)的大小关系是( )A.f(-4)>f(1) B.f(-4)=f(1) C.f(-4)<f(1) D.不能确定19.若
18.函数f(x)=a|x+1|(a>0,且a≠1)的值域为[1,+∞),则f(-4)与f(1)的大小关系是( )A.f(-4)>f(1) B.f(-4)=f(1) C.f(-4)<f(1) D.不能确定19.若![]() ,且
,且![]() ,则
,则![]() 的值等于( )A.
的值等于( )A.![]()
![]() B.
B.![]() C.
C.![]() D.2 20.若a=(2+
D.2 20.若a=(2+![]() )-1,b=(2-
)-1,b=(2-![]() )-1,则(a+1)-2+(b+1)-2的值是( )A.1 B.
)-1,则(a+1)-2+(b+1)-2的值是( )A.1 B.![]() C.
C.![]() D.
D.![]() 二 、填空题21.若函数f(x)=a+
二 、填空题21.若函数f(x)=a+![]() 满足f(-x)=-f(x),则a=_________.22.比较下来各题中两个值的大小: ①1.72.5,1.73; ②0.8-0.1,0.8-0.2; ③1.70.3,0.93.1; ④1.7-0.3,0.9-3.1. .23.方程
满足f(-x)=-f(x),则a=_________.22.比较下来各题中两个值的大小: ①1.72.5,1.73; ②0.8-0.1,0.8-0.2; ③1.70.3,0.93.1; ④1.7-0.3,0.9-3.1. .23.方程![]() 的实数解为 . 24.设5x=4,5y=2,则52x-y=____________.25.
的实数解为 . 24.设5x=4,5y=2,则52x-y=____________.25.![]() .26.已知函数f(x)=
.26.已知函数f(x)=![]() (a>0,a
(a>0,a![]() 1)在区间[0,+∞)上是增函数,则a的取值范围是 27.函数y=(
1)在区间[0,+∞)上是增函数,则a的取值范围是 27.函数y=(![]() )
)![]() (-3
(-3![]() )的值域是28.若指数函数y=ax在[-1,1]上的最大值与最小值的差是1,则底数a= . 29.函数f(x)=
)的值域是28.若指数函数y=ax在[-1,1]上的最大值与最小值的差是1,则底数a= . 29.函数f(x)=![]() 的单调增区间为 ,值域为 .30.已知函数f(x)=ex,若关于x的不等式[f(x)]2-2f(x)-a≥0在[0,1]上有解,则实数a的取值范围为________.
的单调增区间为 ,值域为 .30.已知函数f(x)=ex,若关于x的不等式[f(x)]2-2f(x)-a≥0在[0,1]上有解,则实数a的取值范围为________.
答案解析1.答案为:B 2.答案为:B 3.D.4.D 5.D6.D7.D8.答案为:B 9.答案为:A. 10.答案为:C. 11.B12.答案为:C 13.A.14.答案为:A;解析:选A.∵以P(x1,f(x1)),Q(x2,f(x2))为端点的线段的中点在y轴上,∴x1+x2=0.又∵f(x)=ax,∴f(x1)·f(x2)=ax1·ax2=ax1+x2=a0=1,故选A.15.答案为:A思路解析:∵0<a<1,b<-1,则y=ax+b的图象如下图所示, 由图象可知,函数y=ax+b的图象不经过第一象限. 16.B;17.答案为:D18.A 由题意知a>1,所以f(-4)=a3, f(1)=a2,由y=ax(a>1)的单调性知a3>a2,所以f(-4)>f(1).19.答案为:C;
由图象可知,函数y=ax+b的图象不经过第一象限. 16.B;17.答案为:D18.A 由题意知a>1,所以f(-4)=a3, f(1)=a2,由y=ax(a>1)的单调性知a3>a2,所以f(-4)>f(1).19.答案为:C; 20.D;a=(2+
20.D;a=(2+![]() )-1=2-
)-1=2-![]() ,b=(2-
,b=(2-![]() )-1=2+
)-1=2+![]() ,∴(a+1)-2+(b+1)-2=(3-
,∴(a+1)-2+(b+1)-2=(3-![]() )-2+(3+
)-2+(3+![]() )-2=
)-2=![]() +
+![]() =
=![]() .21.答案为:-0.5;22.答案为:<,<,>,<;23.答案为:log34.24.答案为:8 25.答案为:
.21.答案为:-0.5;22.答案为:<,<,>,<;23.答案为:log34.24.答案为:8 25.答案为:![]() ;原式=
;原式= .26.答案为:
.26.答案为:![]() 27. [(
27. [(![]() )9,39]28.答案
)9,39]28.答案 ![]() 解析 若0<a<1,则a-1-a=1,即a2+a-1=0,解得a=
解析 若0<a<1,则a-1-a=1,即a2+a-1=0,解得a=![]() 或a=
或a=![]() (舍去).若a>1,则a-a-1=1,即a2-a-1=0,解得a=
(舍去).若a>1,则a-a-1=1,即a2-a-1=0,解得a=![]() 或a=
或a=![]() (舍去).综上所述,a=
(舍去).综上所述,a=![]() .29.答案为:(-∞,1],(0,3];30.答案为:(-∞,e2-2e];解析:由[f(x)]2-2f(x)-a≥0在[0,1]上有解,可得a≤[f(x)]2-2f(x),即a≤e2x-2ex.令g(x)=e2x-2ex(0≤x≤1),则a≤g(x)max.因为0≤x≤1,所以1≤ex≤e,则当ex=e,即x=1时,g(x)max=e2-2e,即a≤e2-2e,故实数a的取值范围为(-∞,e2-2e].
.29.答案为:(-∞,1],(0,3];30.答案为:(-∞,e2-2e];解析:由[f(x)]2-2f(x)-a≥0在[0,1]上有解,可得a≤[f(x)]2-2f(x),即a≤e2x-2ex.令g(x)=e2x-2ex(0≤x≤1),则a≤g(x)max.因为0≤x≤1,所以1≤ex≤e,则当ex=e,即x=1时,g(x)max=e2-2e,即a≤e2-2e,故实数a的取值范围为(-∞,e2-2e].
相关试卷
这是一份高考数学二轮复习题海集训34 导数的计算(30题含答案),共6页。
这是一份高考数学二轮复习题海集训32 双曲线(30题含答案),共10页。试卷主要包含了故选C,由左焦点F,等内容,欢迎下载使用。
这是一份高考数学二轮复习题海集训31 椭圆(30题含答案),共9页。










