四川省成都七中2016-2017学年高二（上）期末数学试卷（理科）（解析版）

这是一份四川省成都七中2016-2017学年高二（上）期末数学试卷（理科）（解析版），共25页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2016-2017学年四川省成都七中高二（上）期末数学试卷（理科）
　
一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1．命题p：“a=﹣2”是命题q：“直线ax+3y﹣1=0与直线6x+4y﹣3=0垂直”成立的（　　）
A．充要条件 B．充分非必要条件
C．必要非充分条件 D．既不充分也不必要条件
2．成都七中为了全面落实素质教育，切实有效减轻学生课业负担，拟从林荫、高新两个校区的初高中学生中抽取部分学生进行调查，事先已了解到初中三个年级、高中三个年级学生的课业负担情况有较大差异，而男女生课业负担差异不大．在下面的抽样方法中，最合理的抽样方法是（　　）
A．简单随机抽样 B．按性别分层抽样
C．按年级分层抽样 D．系统抽样
3．圆（x+2）2+y2=4与圆（x﹣2）2+（y﹣1）2=9的位置关系为（　　）
A．内切 B．相交 C．外切 D．相离
4．已知双曲线的离心率为2，那么双曲线的渐近线方程为（　　）
A． B．x±y=0 C．2x±y=0 D．
5．函数f（x）=x2﹣x﹣2，x∈[﹣5，5]，在定义域内任取一点x0，使f（x0）≤0的概率是（　　）
A． B． C． D．
6．设实数x，y满足，则μ=的取值范围是（　　）
A．[，2] B．[，] C．[，2] D．[2，]
7．有5名高中优秀毕业生回母校成都7中参加高2015级励志成才活动，到3个班去做学习经验交流，则每个班至少去一名的不同分派方法种数为（　　）
A．200 B．180 C．150 D．280
8．柜子里有3双不同的鞋，随机地取2只，下列叙述错误的是（　　）
A．取出的鞋不成对的概率是
B．取出的鞋都是左脚的概率是
C．取出的鞋都是同一只脚的概率是
D．取出的鞋一只是左脚的，一只是右脚的，但它们不成对的概率是
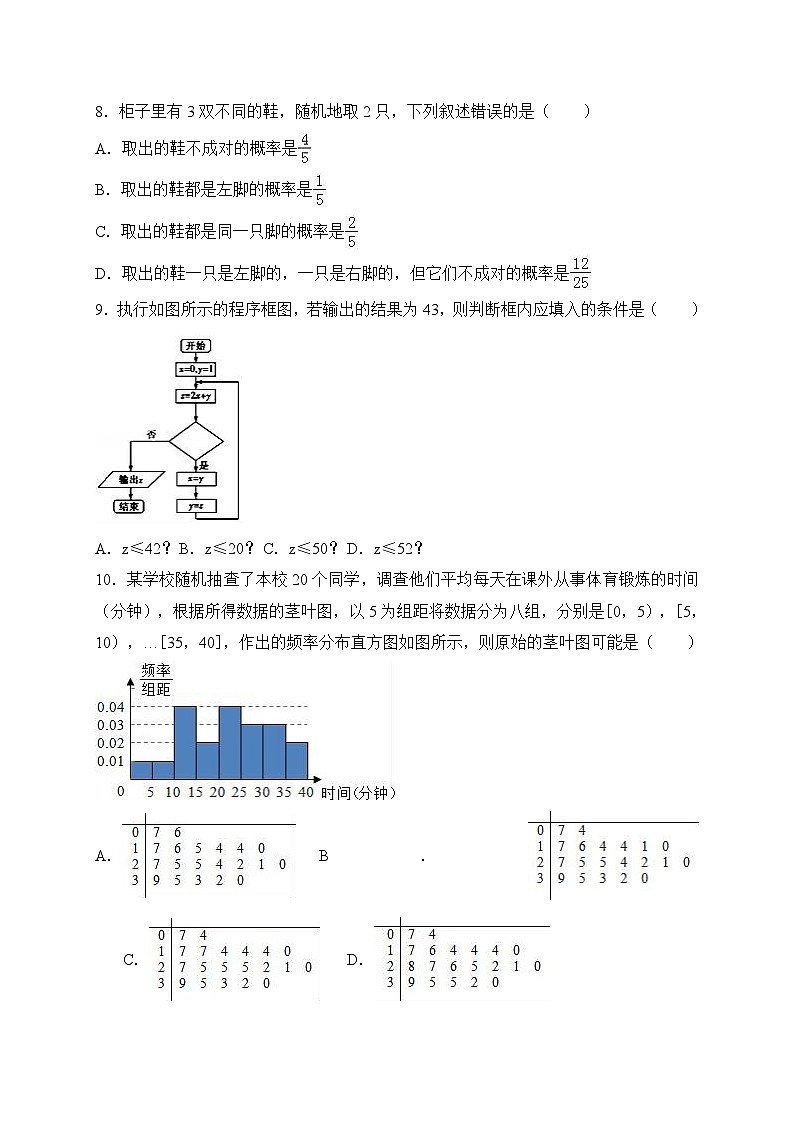
9．执行如图所示的程序框图，若输出的结果为43，则判断框内应填入的条件是（　　）
A．z≤42？ B．z≤20？ C．z≤50？ D．z≤52？
10．某学校随机抽查了本校20个同学，调查他们平均每天在课外从事体育锻炼的时间（分钟），根据所得数据的茎叶图，以5为组距将数据分为八组，分别是[0，5），[5，10），…[35，40]，作出的频率分布直方图如图所示，则原始的茎叶图可能是（　　）

A． B． C． D．
11．如图，在等腰梯形ABCD中，AB∥CD，且AB=2AD，设∠DAB=θ，θ∈（0，），以A，B为焦点且过点D的双曲线的离心率为e1，以C，D为焦点且过点A的椭圆的离心率为e2，则（　　）

A．随着角度θ的增大，e1增大，e1e2为定值
B．随着角度θ的增大，e1减小，e1e2为定值
C．随着角度θ的增大，e1增大，e1e2也增大
D．随着角度θ的增大，e1减小，e1e2也减小
12．以椭圆+=1的顶点为焦点，焦点为顶点的双曲线C，其左、右焦点分别是F1，F2，已知点M坐标为（2，1），双曲线C上点P（x0，y0）（x0＞0，y0＞0）满足=，则﹣S（　　）
A．2 B．4 C．1 D．﹣1
　
二、填空题（每题5分，满分20分，将答案填在答题纸上）
13．命题∀x∈R，|x|＜0的否定是　　．
14．已知双曲线x2﹣my2=1的虚轴长是实轴长的3倍，则实数m的值是　　．
15．在平面直角坐标系xOy中，曲线x2+y2=2|x|+2|y|围成的图形的面积为　　．
16．已知圆C：（x﹣1）2+y2=r2（r＞0）与直线l：y=x+3，且直线l上有唯一的一个点P，使得过点P作圆C的两条切线互相垂直．设EF是直线l上的一条线段，若对于圆C上的任意一点Q，，则的最小值是　　．
　
三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）
17．某市统计局就某地居民的月收入调查了10000人，并根据所得数据画出样本的频率分布直方图，每个分组包括左端点，不包括右端点，如第一组表示收入在[1000，1500）．
（1）求居民收入在[3000，3500）的频率；
（2）根据频率分布直方图算出样本数据的中位数、平均数及其众数；
（3）为了分析居民的收入与年龄、职业等方面的关系，按收入从这10000人中用分层抽样方法抽出100人作进一步分析，则应在月收入为[2500，3000）的人中抽取多少人？

18．口袋中装有4个形状大小完全相同的小球，小球的编号分别为1，2，3，4，甲、乙、丙依次有放回地随机抽取1个小球，取到小球的编号分别为a，b，c．
（1）在一次抽取中，若有两人抽取的编号相同，则称这两人为“好朋友”，求甲、乙两人成为“好朋友”的概率；
（2）求抽取的编号能使方程a+b+2c=6成立的概率．
19．某科研所对新研发的一种产品进行合理定价，该产品按事先拟定的价格试销得统计数据．
单价x（万元）
8
8.2
8.4
8.8
8.6
9
销量y（件）
90
84
83
75
80
68
（1）①求线性回归方程y=x+；②谈谈商品定价对市场的影响；
（2）估计在以后的销售中，销量与单价服从回归直线，若该产品的成本为4.5元/件，为使科研所获利最大，该产品定价应为多少？
（附： =， =﹣， =8.5， =80）
20．已知⊙C：x2+y2﹣2x﹣4y﹣20=0，直线l：（2m+1）x+（m+1）y﹣7m﹣4=0．
（1）求证：直线l与⊙C恒有两个交点；
（2）若直线l与⊙C的两个不同交点分别为A，B．求线段AB中点P的轨迹方程，并求弦AB的最小值．
21．已知一条曲线C在y轴右边，C上每一点到点F（1，0）的距离减去它到y轴距离的差都是1．
（1）求曲线C的方程；
（2）是否存在整数m，对于过点M（m，0）且与曲线C有两个交点A，B的任一直线，都有|FA|2+|FB|2＜|AB|2？若存在，求出m的取值范围；若不存在，请说明理由．
22．已知椭圆的上顶点M与左、右焦点F1，F2构成三角形MF1F2面积为，又椭圆C的离心率为，左右顶点分别为P，Q．
（1）求椭圆C的方程；
（2）过点D（m，0）（m∈（﹣2，2），m≠0）作两条射线分别交椭圆C于A，B两点（A，B在长轴PQ同侧），直线AB交长轴于点S（n，0），且有∠ADP=∠BDQ．求证：mn为定值；
（3）椭圆C的下顶点为N，过点T（t，2）（t≠0）的直线TM，TN分别与椭圆C交于E，F两点．若△TMN的面积是△TEF的面积的λ倍，求λ的最大值．

　

2016-2017学年四川省成都七中高二（上）期末数学试卷（理科）
参考答案与试题解析
　
一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1．命题p：“a=﹣2”是命题q：“直线ax+3y﹣1=0与直线6x+4y﹣3=0垂直”成立的（　　）
A．充要条件 B．充分非必要条件
C．必要非充分条件 D．既不充分也不必要条件
【考点】必要条件、充分条件与充要条件的判断．
【分析】根据直线垂直的等价条件，结合充分条件和必要条件的定义进行判断即可．
【解答】解：若“直线ax+3y﹣1=0与直线6x+4y﹣3=0垂直”，则6a+3×4=0，解得a=﹣2，
故p是q成立的充要条件，
故选：A
　
2．成都七中为了全面落实素质教育，切实有效减轻学生课业负担，拟从林荫、高新两个校区的初高中学生中抽取部分学生进行调查，事先已了解到初中三个年级、高中三个年级学生的课业负担情况有较大差异，而男女生课业负担差异不大．在下面的抽样方法中，最合理的抽样方法是（　　）
A．简单随机抽样 B．按性别分层抽样
C．按年级分层抽样 D．系统抽样
【考点】收集数据的方法．
【分析】若总体由差异明显的几部分组成时，经常采用分层抽样的方法进行抽样．
【解答】解：事先已了解到初中三个年级、高中三个年级学生的课业负担情况有较大差异，而男女生课业负担差异不大，按年级分层抽样，这种方式具有代表性，比较合理．
故选：C．
　
3．圆（x+2）2+y2=4与圆（x﹣2）2+（y﹣1）2=9的位置关系为（　　）
A．内切 B．相交 C．外切 D．相离
【考点】圆与圆的位置关系及其判定．
【分析】求出两圆的圆心和半径，计算两圆的圆心距，将圆心距和两圆的半径之和或半径之差作对比，判断两圆的位置关系．
【解答】解：圆（x+2）2+y2=4的圆心C1（﹣2，0），半径r=2．
圆（x﹣2）2+（y﹣1）2=9的圆心C2（2，1），半径R=3，
两圆的圆心距d==，
R+r=5，R﹣r=1，
R+r＞d＞R﹣r，
所以两圆相交，
故选B．
　
4．已知双曲线的离心率为2，那么双曲线的渐近线方程为（　　）
A． B．x±y=0 C．2x±y=0 D．
【考点】双曲线的简单性质．
【分析】利用双曲线的离心率，转化求出a，b关系，即可求解双曲线的渐近线方程．
【解答】解：双曲线的离心率为2，
可得，即，可得，
双曲线的渐近线方程为：y=±，
即．
故选：D．
　
5．函数f（x）=x2﹣x﹣2，x∈[﹣5，5]，在定义域内任取一点x0，使f（x0）≤0的概率是（　　）
A． B． C． D．
【考点】几何概型；一元二次不等式的解法．
【分析】先解不等式f（x0）≤0，得能使事件f（x0）≤0发生的x0的取值长度为3，再由x0总的可能取值，长度为定义域长度10，得事件f（x0）≤0发生的概率是0.3
【解答】解：∵f（x）≤0⇔x2﹣x﹣2≤0⇔﹣1≤x≤2，
∴f（x0）≤0⇔﹣1≤x0≤2，即x0∈[﹣1，2]，
∵在定义域内任取一点x0，
∴x0∈[﹣5，5]，
∴使f（x0）≤0的概率P==
故选C
　
6．设实数x，y满足，则μ=的取值范围是（　　）
A．[，2] B．[，] C．[，2] D．[2，]
【考点】简单线性规划．
【分析】根据不等式组画出可行域，得到如图所示的△ABC及其内部的区域．设P（x，y）为区域内一点，根据斜率计算公式可得μ=表示直线OP的斜率，运动点P得到PQ斜率的最大、最小值，即可得到μ=的取值范围．
【解答】解：作出不等式组表示的平面区域，得到如图所示的△ABC及其内部的区域
其中A（1，2），B（4，2），C（3，1）
设P（x，y）为区域内的动点，可得μ=表示直线OP的斜率，
其中P（x，y）在区域内运动，O是坐标原点．
运动点P，可得当P与A点重合时，μ=2达到最大值；
当P与C点重合时，μ=达到最小值．
综上所述，μ=的取值范围是[，2]
故选：A

　
7．有5名高中优秀毕业生回母校成都7中参加高2015级励志成才活动，到3个班去做学习经验交流，则每个班至少去一名的不同分派方法种数为（　　）
A．200 B．180 C．150 D．280
【考点】排列、组合的实际应用．
【分析】根据题意，分2步进行分析，①、先将5个人分成3组，分析可得有2种分组方法：分成2﹣2﹣1的三组或分成3﹣1﹣1的三组，分别求出每种情况的分组方法数目，由分类计数原理可得分组方法数目，②、将分好的3组对应三个班级，由排列数公式可得其方法数目，进而由分步计数原理计算可得答案．
【解答】解：根据题意，分2步进行分析，
①、先将5个人分成3组，
若分成2﹣2﹣1的三组，有=15种情况，
若分成3﹣1﹣1的三组，有=10种情况，
一共有15+10=25种分组方法；
②、将分好的3组对应三个班级，有=6种方法，
则一共有25×6=150种不同分派方法，
故选：C．
　
8．柜子里有3双不同的鞋，随机地取2只，下列叙述错误的是（　　）
A．取出的鞋不成对的概率是
B．取出的鞋都是左脚的概率是
C．取出的鞋都是同一只脚的概率是
D．取出的鞋一只是左脚的，一只是右脚的，但它们不成对的概率是
【考点】古典概型及其概率计算公式．
【分析】利用等可能事件概率计算公式分别求解，能求出结果．
【解答】解：∵柜子里有3双不同的鞋，随机地取2只，
∴基本事件总数n==15，
在A中，取出的鞋是成对的取法有3种，
∴取出的鞋不成对的概率是：1﹣=，故A 正确；
在B中，取出的鞋都是左脚的取法有=3种，
∴取出的鞋都是左脚的概率为：，故B正确；
在C中，取出的鞋都是同一只脚的取法有： =6，
∴取出的鞋都是同一只脚的概率是p==；
在D中，取出的鞋一只是左脚的，一只是右脚的，
由题意，可以先选出左脚的一只有=3种选法，
然后从剩下两双的右脚中选出一只有=2种选法，
所以一共6种取法，
∴取出的鞋一只是左脚的，一只是右脚的，但它们不成对的概率是，故D错误．
故选：D．
　
9．执行如图所示的程序框图，若输出的结果为43，则判断框内应填入的条件是（　　）
A．z≤42？ B．z≤20？ C．z≤50？ D．z≤52？
【考点】程序框图．
【分析】根据已知中的程序框图可得，该程序的功能是计算并输出变量z的值，模拟程序的运行过程，可得答案．
【解答】解：第一次执行z=2x+y后，z=1，不满足输出条件，应满足进行循环的条件，则x=1，y=1，
第二 次执行z=2x+y后，z=3，不满足输出条件，应满足进行循环的条件，则x=1，y=3，
第三次执行z=2x+y后，z=5，不满足输出条件，应满足进行循环的条件，则x=3，y=5，
第四次执行z=2x+y后，z=11，不满足输出条件，应满足进行循环的条件，则x=5，y=11，
第五次执行z=2x+y后，z=21，不满足输出条件，应满足进行循环的条件，则x=11，y=21，
第六次执行z=2x+y后，z=43，满足输出条件，
故进行循环的条件可以为z≤42？，
故选：A
　
10．某学校随机抽查了本校20个同学，调查他们平均每天在课外从事体育锻炼的时间（分钟），根据所得数据的茎叶图，以5为组距将数据分为八组，分别是[0，5），[5，10），…[35，40]，作出的频率分布直方图如图所示，则原始的茎叶图可能是（　　）

A． B． C． D．
【考点】频率分布直方图；茎叶图．
【分析】由频率分布直方图可得，[25，30），[30，35）的频率相同，频数为3，即可得出结论．
【解答】解：由频率分布直方图可得，[25，30），[30，35）的频率相同，频数为3，
故选：B．
　
11．如图，在等腰梯形ABCD中，AB∥CD，且AB=2AD，设∠DAB=θ，θ∈（0，），以A，B为焦点且过点D的双曲线的离心率为e1，以C，D为焦点且过点A的椭圆的离心率为e2，则（　　）

A．随着角度θ的增大，e1增大，e1e2为定值
B．随着角度θ的增大，e1减小，e1e2为定值
C．随着角度θ的增大，e1增大，e1e2也增大
D．随着角度θ的增大，e1减小，e1e2也减小
【考点】椭圆的简单性质．
【分析】连接BD、AC，假设AD=t，根据余弦定理表示出BD，进而根据双曲线的性质可得到a的值，再由AB=2c，e=可表示出e1=，最后根据余弦函数的单调性可判断e1的单调性；同样表示出椭圆中的c'和a'表示出e2的关系式，最后令e1、e2相乘即可得到e1e2的关系．
【解答】解：连接BD，AC设AD=t，则BD==
∴双曲线中a=
e1=
∵y=cosθ在（0，）上单调减，进而可知当θ增大时，y==减小，即e1减小
∵AC=BD
∴椭圆中CD=2t（1﹣cosθ）=2c∴c'=t（1﹣cosθ）
AC+AD=+t，∴a'=（+t）
e2==
∴e1e2=×=1
故选B．

　
12．以椭圆+=1的顶点为焦点，焦点为顶点的双曲线C，其左、右焦点分别是F1，F2，已知点M坐标为（2，1），双曲线C上点P（x0，y0）（x0＞0，y0＞0）满足=，则﹣S（　　）
A．2 B．4 C．1 D．﹣1
【考点】椭圆的简单性质．
【分析】通过已知条件，写出双曲线方程，结合已知等式及平面几何知识得出点M是△F1PF2的内心，利用三角形面积计算公式计算即可．
【解答】解：∵椭圆方程为+=1，
∴其顶点坐标为（3，0）、（﹣3，0），焦点坐标为（2，0）、（﹣2，0），
∴双曲线方程为，
设点P（x，y），记F1（﹣3，0），F2（3，0），
∵=，
∴=，
整理得： =5，
化简得：5x=12y﹣15，
又∵，
∴5﹣4y2=20，
解得：y=或y=（舍），
∴P（3，），
∴直线PF1方程为：5x﹣12y+15=0，
∴点M到直线PF1的距离d==1，
易知点M到x轴、直线PF2的距离都为1，
结合平面几何知识可知点M（2，1）就是△F1PF2的内心．
故﹣===2，
故选：A．

　
二、填空题（每题5分，满分20分，将答案填在答题纸上）
13．命题∀x∈R，|x|＜0的否定是　∃x0∈R，|x0|≥0　．
【考点】命题的否定．
【分析】利用全称命题的否定是特称命题，去判断．
【解答】解：因为命题是全称命题，根据全称命题的否定是特称命题，
所以命题的否定：∃x0∈R，|x0|≥0．
故答案为：∃x0∈R，|x0|≥0．
　
14．已知双曲线x2﹣my2=1的虚轴长是实轴长的3倍，则实数m的值是　　．
【考点】双曲线的简单性质．
【分析】利用双曲线x2﹣my2=1的虚轴长是实轴长的3倍，列出方程求解即可．
【解答】解：双曲线x2﹣my2=1的虚轴长是实轴长的3倍，
可得： =3，解得m=．
故答案为：．
　
15．在平面直角坐标系xOy中，曲线x2+y2=2|x|+2|y|围成的图形的面积为　6π+8　．
【考点】圆的一般方程．
【分析】x＞0，y＞0时，方程化为（x﹣1）2+（y﹣1）2=2，其面积为=+2，根据图象的对称性，可得曲线x2+y2=2|x|+2|y|围成的图形的面积．
【解答】解：x＞0，y＞0时，方程化为（x﹣1）2+（y﹣1）2=2，其面积为=+2
根据图象的对称性，可得曲线x2+y2=2|x|+2|y|围成的图形的面积为6π+8，
故答案为6π+8．
　
16．已知圆C：（x﹣1）2+y2=r2（r＞0）与直线l：y=x+3，且直线l上有唯一的一个点P，使得过点P作圆C的两条切线互相垂直．设EF是直线l上的一条线段，若对于圆C上的任意一点Q，，则的最小值是　4+4　．
【考点】直线和圆的方程的应用．
【分析】由圆的对称性知直线l上的唯一点P与圆心C（1，0）所在直线必与直线l垂直，求得PC所在直线方程，与直线l求得交点P，再根据对称性可得r=2，由题意，知|EF|取得最小值时，一定关于直线y=﹣x+1对称，画出图形，通过图形观察，当两圆相内切时，求得最小值．
【解答】解：根据圆的对称性知直线l上的唯一点P与圆心C（1，0）所在直线必与直线l垂直，
则PC所在直线的方程为x+y=1，与直线y=x+3联立求得P（﹣1，2），
再根据对称性知过点P（﹣1，2）的两条切线必与坐标轴垂直，r=2；
由题意，知|EF|取得最小值时，一定关于直线y=﹣x+1对称，如图所示，
因此可设以点P（﹣1，2）为圆心，以R为半径的圆，
即（x+1）2+（y﹣2）2=R2与圆C内切时，
的最小值即为2R，
由相切条件易知2R=2（|CP|+2）=2（2+2）=4+4．
故答案为：4+4．

　
三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）
17．某市统计局就某地居民的月收入调查了10000人，并根据所得数据画出样本的频率分布直方图，每个分组包括左端点，不包括右端点，如第一组表示收入在[1000，1500）．
（1）求居民收入在[3000，3500）的频率；
（2）根据频率分布直方图算出样本数据的中位数、平均数及其众数；
（3）为了分析居民的收入与年龄、职业等方面的关系，按收入从这10000人中用分层抽样方法抽出100人作进一步分析，则应在月收入为[2500，3000）的人中抽取多少人？

【考点】频率分布直方图．
【分析】（1）根据频率=小矩形的高×组距来求；
（2）根据中位数的左右两边的矩形的面积和相等，所以只需求出从左开始面积和等于0.5的底边横坐标的值即可，运用取中间数乘频率，再求之和，计算可得平均数，求出众数即可；
（3）求出月收入在[2500，3000）的人数，用分层抽样的抽取比例乘以人数，可得答案．
【解答】解：（1）月收入在[3000，3500）的频率为0.0003×500=0.15；
（2）从左数第一组的频率为0.0002×500=0.1；
第二组的频率为0.0004×500=0.2；
第三组的频率为0.0005×500=0.25；
∴中位数位于第三组，设中位数为2000+x，则x×0.0005=0.5﹣0.1﹣0.2=0.2⇒x=400．
∴中位数为2400（元）
由1250×0.1+1750×0.2+2250×0.25+2750×0.25+3250×0.15+3750×0.05=2400，
样本数据的平均数为2400（元）；
众数是： =2250，和=2750；
（3）月收入在[2500，3000）的频数为0.25×10000=2500（人），
∵抽取的样本容量为100．∴抽取比例为 =，
∴月收入在[2500，3000）的这段应抽取2500×=25（人）．
　
18．口袋中装有4个形状大小完全相同的小球，小球的编号分别为1，2，3，4，甲、乙、丙依次有放回地随机抽取1个小球，取到小球的编号分别为a，b，c．
（1）在一次抽取中，若有两人抽取的编号相同，则称这两人为“好朋友”，求甲、乙两人成为“好朋友”的概率；
（2）求抽取的编号能使方程a+b+2c=6成立的概率．
【考点】列举法计算基本事件数及事件发生的概率．
【分析】（1）将甲、乙依次取到小球的编号记为（a，b），利用列出法求出基本事件个数和甲、乙两人成为好朋友包含的情况种数，由此能求出甲、乙两人成为“好朋友”的概率．
（2）将甲、乙、丙依次取到小球的编号记为（a，b，c），求出基本事件个数，利用列举法求出丙抽取的编号能使方程a+b+2c=6成立包含的基本事件个数，由此能求出抽取的编号能使方程a+b+2c=6成立的概率．
【解答】解：（1）将甲、乙依次取到小球的编号记为（a，b），
则基本事件有（1，1），（1，2），（1，3），（1，4），（2，1），
（2，2），（2，3），（2，4），（3，1），（3，2），（3，3），
（3，4），（4，1），（4，2），（4，3），（4，4），共16个．
记“甲、乙两人成为好朋友”为事件M，则M包含的情况有：
（1，1），（2，2），（3，3），（4，4），共4个人，
故甲、乙两人成为“好朋友”的概率为P（M）==．
（2）将甲、乙、丙依次取到小球的编号记为（a，b，c），
则基本事件有n=4×4×4=64个，
记“丙抽取的编号能使方程a+b+2c=6成立”为事件N，
当丙抽取的编号c=1时，工+子4，
∴（a，b）分别为（1，3），（2，2），（3，1），
当丙抽取的编号c=2时，a+b=2，∴（a，b）为（1，1），
当丙抽取的编号c=3或c=4时，方程a+b+2c=6不成立．
综上，事件N包含的基本事件有4个，
∴．
　
19．某科研所对新研发的一种产品进行合理定价，该产品按事先拟定的价格试销得统计数据．
单价x（万元）
8
8.2
8.4
8.8
8.6
9
销量y（件）
90
84
83
75
80
68
（1）①求线性回归方程y=x+；②谈谈商品定价对市场的影响；
（2）估计在以后的销售中，销量与单价服从回归直线，若该产品的成本为4.5元/件，为使科研所获利最大，该产品定价应为多少？
（附： =， =﹣， =8.5， =80）
【考点】线性回归方程．
【分析】（1）①根据公式求出和的值，求出回归方程即可；②根据b的值判断即可；（2）求出关于w的表达式，结合二次函数的性质求出w的最大值即可．
【解答】解：（1）①依题意： ==﹣20，
=﹣=80+20×8.5=250，
∴回归直线的方程为y=﹣20x+250；
②由于=﹣20＜0，则x，y负相关，
故随定价的增加，销量不断降低．
（2）设科研所所得利润为w，设定价为x，
∴w=（x﹣4.5）（﹣20x+250）=﹣20x2+340x﹣1125，
∴当时，wmax=320，
故当定价为8.5元时，w取得最大值．
　
20．已知⊙C：x2+y2﹣2x﹣4y﹣20=0，直线l：（2m+1）x+（m+1）y﹣7m﹣4=0．
（1）求证：直线l与⊙C恒有两个交点；
（2）若直线l与⊙C的两个不同交点分别为A，B．求线段AB中点P的轨迹方程，并求弦AB的最小值．
【考点】直线和圆的方程的应用．
【分析】（1）求出圆C的圆心和半径，整理直线方程为m（2x+y﹣7）+（x+y﹣4）=0，求出直线2x+y﹣7=0，x+y﹣4=0的交点，判断它在圆内，即可得证；
（2）由题意知，设点P（x，y）为弦AB的中点，连接CP，则CP⊥PQ，由平面几何知识可得点P的轨迹方程是以CQ为直径的圆，求得圆心和半径，注意运用中点坐标公式，再由当Q（3，1）是弦AB的中点时，|AB|最小，运用勾股定理即可得到所求值．
【解答】解：（1）证明：⊙C：x2+y2﹣2x﹣4y﹣20=0，
即（x﹣1）2+（y﹣2）2=25，圆心C（1，2），半径r=5，
又直线l：（2m+1）x+（m+1）y﹣7m﹣4=0，
化为m（2x+y﹣7）+（x+y﹣4）=0，
由解得，
则直线l恒过定点Q（3，1），
由|CQ|==＜5，
可得Q在圆C内，则直线l与⊙C恒有两个交点；
（2）由题意知，设点P（x，y）为弦AB的中点，
由（1）可知CP⊥PQ，
点P的轨迹方程是以CQ为直径的圆，
线段CQ的中点为（2，），|CQ|=，
则线段AB中点P的轨迹方程为；
由圆的几何性质可知，当Q（3，1）是弦AB的中点时，|AB|最小．
弦心距，⊙C的半径为5，
可得|AB|min=2=4．
　
21．已知一条曲线C在y轴右边，C上每一点到点F（1，0）的距离减去它到y轴距离的差都是1．
（1）求曲线C的方程；
（2）是否存在整数m，对于过点M（m，0）且与曲线C有两个交点A，B的任一直线，都有|FA|2+|FB|2＜|AB|2？若存在，求出m的取值范围；若不存在，请说明理由．
【考点】直线与抛物线的位置关系．
【分析】（1）设P（x，y）（x＞0）是曲线C上任意一点，列出方程求解即可．
（2）设过点M（m，0）（m＞0）的直线l与曲线C的交点为A（x1，y1），B（x2，y2）．设l的方程为x=λy+m，联立利用韦达定理，结合向量的数量积推出m2﹣6m+1＜4λ2，对任意实数λ，4λ2的最小值为0，转化求解即可得到m的取值范围．
【解答】解：（1）设P（x，y）（x＞0）是曲线C上任意一点，
那么点P（x，y）满足：，
化简得y2=4x（x＞0）．
（2）设过点M（m，0）（m＞0）的直线l与曲线C的交点为A（x1，y1），B（x2，y2）．
设l的方程为x=λy+m，由得y2﹣4λy﹣4m=0，△=16（λ2+m）＞0，
于是①，又，②，
又，于是不等式②等价于③，
由①式，不等式③等价于m2﹣6m+1＜4λ2④对任意实数λ，4λ2的最小值为0，
所以不等式④对于一切π成立等价于m2﹣6m+1＜0，即．
由此可知，存在正数m，对于过点M（m，0）且与曲线C有两个交点A，B的任一直线，
都有|FA|2+|FB|2＜|AB|2，且m的取值范围为．
　
22．已知椭圆的上顶点M与左、右焦点F1，F2构成三角形MF1F2面积为，又椭圆C的离心率为，左右顶点分别为P，Q．
（1）求椭圆C的方程；
（2）过点D（m，0）（m∈（﹣2，2），m≠0）作两条射线分别交椭圆C于A，B两点（A，B在长轴PQ同侧），直线AB交长轴于点S（n，0），且有∠ADP=∠BDQ．求证：mn为定值；
（3）椭圆C的下顶点为N，过点T（t，2）（t≠0）的直线TM，TN分别与椭圆C交于E，F两点．若△TMN的面积是△TEF的面积的λ倍，求λ的最大值．

【考点】直线与圆锥曲线的综合问题；椭圆的标准方程；直线与椭圆的位置关系．
【分析】（1）利用椭圆离心率三角形的面积，解得a，b，即可得到椭圆方程．
（2）设AB：y=k（x﹣n）（k≠0），A（x1，y1），B（x2，y2）．联立直线与椭圆方程，利用韦达定理以及斜率关系，推出结果即可．
（3）设E（x3，y3），F（x4，y4），通过，直线TM方程为：x=t（y﹣1），直线TN：3x﹣ty﹣t=0，联立直线与椭圆方程，求出E，F坐标，求出E到直线TN：3x﹣ty﹣t=0的距离，推出两个三角形的面积，利用基本不等式求解即可．
【解答】解：（1）椭圆离心率，又，解得a=2，b=1，
∴椭圆．
（2）由已知AB必有斜率，设AB：y=k（x﹣n）（k≠0），A（x1，y1），B（x2，y2）．
联立.
⇒k（x1﹣n）（x2﹣m）+k（x1﹣m）（x2﹣m）=0⇒2x1x2﹣（m+n）（x1+x2）+2mn=0⇒mn=4．
（3）设E（x3，y3），F（x4，y4），因为，
直线TM方程为：x=t（y﹣1），直线TN：3x﹣ty﹣t=0，
联立，
联立，
所以E到直线TN：3x﹣ty﹣t=0的距离，，
∴，
（取等条件），
λ的最大值为．
　

2017年3月7日