2024届高考数学一轮复习第6章第7节立体几何中的向量方法——求空间角与距离学案

这是一份2024届高考数学一轮复习第6章第7节立体几何中的向量方法——求空间角与距离学案，共47页。学案主要包含了教材概念·结论·性质重现，基本技能·思想·活动经验等内容，欢迎下载使用。

第七节　立体几何中的向量方法——求空间角与距离
考试要求：1．能用向量方法解决点到直线、点到平面、相互平行的直线、相互平行的平面的距离问题和简单夹角问题．
2．了解向量方法在研究立体几何问题中的应用．

一、教材概念·结论·性质重现
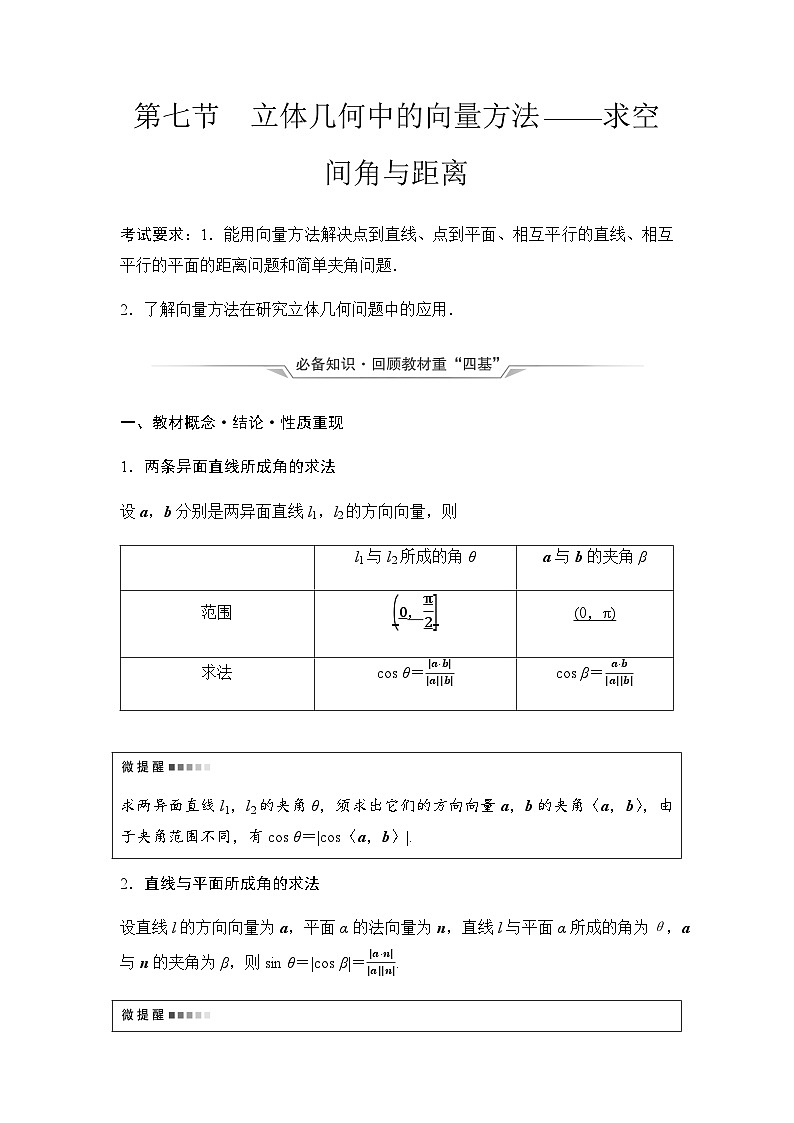
1．两条异面直线所成角的求法
设a，b分别是两异面直线l1，l2的方向向量，则

l1与l2所成的角θ
a与b的夹角β
范围
0，π2
(0，π)
求法
cos θ＝a·bab
cos β＝a·bab


求两异面直线l1，l2的夹角θ，须求出它们的方向向量a，b的夹角〈a，b〉，由于夹角范围不同，有cos θ＝|cos〈a，b〉|.
2．直线与平面所成角的求法
设直线l的方向向量为a，平面α的法向量为n，直线l与平面α所成的角为θ，a与n的夹角为β，则sin θ＝|cos β|＝a·nan.

求直线l与平面α所成的角θ，可先求出平面α的法向量n与直线l的方向向量a的夹角，则sin θ＝|cos〈n，a〉|.
3．二面角的平面角求法
(1)如图(1)，AB，CD分别是二面角α-l-β的两个半平面内与棱l垂直的直线，则二面角的大小θ＝〈AB，CD〉.

(2)如图(2)(3)，n1，n2分别是二面角α-l-β的两个半平面α，β的法向量，则二面角θ的大小满足|cos θ|＝|cos 〈n1，n2〉|，二面角的平面角的大小是向量n1与n2的夹角(或其补角)．

利用平面的法向量求二面角的大小时，求出两平面α，β的法向量n1，n2后，要根据向量坐标在图形中观察法向量的方向，从而确定二面角与向量n1，n2的夹角是相等，还是互补．一进一出相等，同进同出互补．
4．利用空间向量求距离
(1)点到直线的距离
如图所示，

已知直线l的单位方向向量为u，A是直线l上的定点，P是直线l外一点，则点P到直线l的距离PQ＝AP2-AP·u2．
(2)点到平面的距离
如图所示，

已知AB为平面α的一条斜线段，n为平面α的法向量，则点B到平面α的距离为BO＝AB·nn．

求点到平面的距离，若用向量知识，则离不开以该点为端点的平面的斜线段．有时利用等积法求解可能更方便．
二、基本技能·思想·活动经验
1．判断下列说法的正误，对的画“√”，错的画“×”．
(1)两直线的方向向量所成的角就是两条直线所成的角． (　×　)
(2)直线的方向向量和平面的法向量所成的角就是直线与平面所成的角．(　×　)
(3)两个平面的法向量所成的角是这两个平面所成的角． (　×　)
(4)两异面直线夹角的范围是0，π2，直线与平面所成角的范围是0，π2，二面角的范围是[0，π]. (　√　)
2．已知两平面的法向量分别为m＝(0，1，0)，n＝(0，1，1)，则两平面所成的二面角为(　　)
A．45° B．135°
C．45°或135° D．90°
C　解析：cos 〈m，n〉＝m·nmn＝11×2＝22，即〈m，n〉＝45°.
所以两平面所成二面角为45°或180°－45°＝135°.
3．如图，在正方体ABCD-A1B1C1D1中，已知M，N分别是BD和AD的中点，则B1M与D1N所成角的余弦值为(　　)

A．3010 B．3015
C．3030 D．1515
A　解析：以D为原点，DA，DC，DD1所在直线分别为x轴、y轴、z轴建立如图所示空间直角坐标系．

设AB＝2，则N(1，0，0)，D1(0，0，2)，M(1，1，0)，B1(2，2，2)，
所以B1M＝(－1，－1，－2)，
D1N＝(1，0，－2)，
所以B1M·D1N＝－1＋4＝3，
|B1M|＝6，|D1N|＝5，
所以cos 〈B1M，D1N〉＝330＝3010，
所以B1M与D1N所成角的余弦值为3010.故选A．
4．如图所示，在四棱锥P­ABCD中，侧面PAD⊥底面ABCD，侧棱PA＝PD＝2，PA⊥PD，底面ABCD为直角梯形，其中BC∥AD，AB⊥AD，AB＝BC＝1，O为AD的中点．

(1)直线PB与平面POC所成角的余弦值为________；
(2)点B到平面PCD的距离为________．
63　33　解析：(1)在△PAD中，PA＝PD，O为AD中点，所以PO⊥AD．
又侧面PAD⊥底面ABCD，平面PAD∩平面ABCD＝AD，PO⊂平面PAD，
所以PO⊥平面ABCD．
又在直角梯形ABCD中，易得OC⊥AD．
以O为原点，OC为x轴，OD为y轴，OP为z轴建立空间直角坐标系．

则P(0，0，1)，A(0，－1，0)，B(1，－1，0)，C(1，0，0)，D(0，1，0)，
所以PB＝(1，－1，－1)．
因为OA⊥PO， OA⊥CO， PO∩CO=O，得OA⊥平面POC，
所以OA＝(0，－1，0)是平面POC的一个法向量，
所以cos 〈PB，OA〉＝PB·OAPBOA＝33，
所以1-cos2〈PB，OA〉＝63，
所以直线PB与平面POC所成角的余弦值为63.
(2)PB＝(1，－1，－1), 设平面PDC的法向量为n＝(x，y，z)，
则n·CP=x，y，z·-1，0，1=-x+z=0，n·PD=x，y，z·0，1，-1=y-z=0，
取z＝1得n＝(1，1，1)为平面PCD的一个法向量，
点B到平面PCD的距离d＝BP·nn＝33.
5．过正方形ABCD的顶点A作线段PA⊥平面ABCD，若AB＝PA，则平面ABP与平面CDP的夹角为________．
45°　解析：如图，建立空间直角坐标系，设AB＝PA＝1，则A(0，0，0)，D(0，1，0)，P(0，0，1)．

由题意，知AD⊥平面PAB，设E为PD的中点，连接AE，则AE⊥PD．又CD⊥平面PAD，所以CD⊥AE，从而AE⊥平面PCD．所以AD＝(0，1，0)，AE＝0，12，12分别是平面PAB，平面PCD的法向量，且〈AD，AE〉＝45°.故平面PAB与平面PCD的夹角为45°.


考点1　异面直线所成的角——基础性

1．在正方体ABCD­A1B1C1D1中，点E，F分别是BB1，D1B1的中点，则EF与A1D所成角的大小为(　　)
A．60° B．90°
C．45° D．75°
B　解析：如图所示，以D为坐标原点，以DA所在直线为x轴，DC所在直线为y轴，DD1所在直线为z轴建立空间直角坐标系．

设正方体ABCD­A1B1C1D1的棱长为2，易得E(2，2，1)，F(1，1，2)，D(0，0，0)，A1(2，0，2)，所以EF＝(－1，－1，1)，DA1＝(2，0，2)，所以EF·DA1＝－2＋2＝0，所以EF⊥DA1.故选B．
2．如图，在四棱锥A­BCDE中，DE∥CB，BE⊥平面ABC，BE＝3，AB＝CB＝AC＝2DE＝2，则异面直线DC与AE所成角的余弦值为(　　)

A．13013 B．21313
C．1313 D．13026
A　解析：如图所示，取BC的中点F，连接AF，DF，可得DF∥BE.因为BE⊥平面ABC，所以DF⊥平面ABC．又由AB＝CB＝AC且F为BC的中点，所以AF⊥BC，故以F为坐标原点，以FA，FB，FD所在直线分别为x，y，z轴，建立空间直角坐标系，如图所示．

则A(3，0，0)，E(0，1，3)，C(0，－1，0)，D(0，0，3)，故CD＝(0, 1, 3)，AE＝(－3， 1, 3)，则cos 〈CD， AE〉＝CD·AECDAE＝1010×13＝13013.所以异面直线DC与AE所成角的余弦值为13013.故选A．
3．如图所示，在棱长为2的正方体ABCD­A1B1C1D1中，E是棱CC1的中点，F是棱AD上一点，AF＝λAD.若异面直线D1E和A1F所成角的余弦值为3210，则λ的值为13．


利用向量法求异面直线所成角的问题，关键是建立空间直角坐标系写出相关点的坐标，并进一步求出相关的向量，利用向量的夹角公式求解．在求解过程中易出现因忽视异面直线所成角的范围而致错的情况.

考点2　 直线与平面所成的角——综合性

(2022·全国甲卷)在四棱锥P­ABCD中，PD⊥底面ABCD，CD∥AB，AD＝DC＝CB＝1，AB＝2，DP＝3.
(1)证明：BD⊥PA．
(2)求PD与平面PAB所成的角的正弦值．

(1)证明：因为PD⊥底面ABCD，BD⊂平面ABCD，
所以PD⊥BD，
取AB中点E，连接DE，
因为AD＝DC＝CB＝1，AB＝2，
所以∠DAB＝60°，
又因为AE＝12AB＝AD＝1，
所以DE＝1，所以DE＝12AB，
所以△ABD为直角三角形，且AB为斜边，
所以BD⊥AD，
又PD∩AD＝D，PD⊂平面PAD，AD⊂平面PAD，
所以BD⊥平面PAD，
又PA⊂平面PAD，
所以BD⊥PA．
(2)解：由(1)知，PD，AD，BD两两互相垂直，故建立如图所示的空间直角坐标系，

BD＝AB2-AD2＝3，
则D(0，0，0)，A(1，0，0)，B(0，3，0)，P(0，0，3)，
所以PD＝(0，0，－3)，PA＝(1，0，－3)，AB＝(－1，3，0)，
设平面PAB的一个法向量为n＝(x，y，z)，则n·PA=x-3z=0， n·AB=-x+3y=0，则可取n＝(3，1，1)，
设PD与平面PAB所成的角为θ，则sin θ＝|cos PD，n|＝PD·nPDn＝55，
所以PD与平面PAB所成的角的正弦值为55.

利用向量求线面角的2种方法
(1)分别求出斜线和它所在平面内的射影直线的方向向量，转化为求两个方向向量的夹角(或其补角)．
(2)通过平面的法向量来求，即求出斜线的方向向量与平面的法向量所夹的锐角，取其余角就是斜线与平面所成的角．

1．在长方体ABCD­A1B1C1D1中，AB＝2，BC＝AA1＝1，则D1C1与平面A1BC1所成角的正弦值为________．
13　解析：建立如图所示的空间直角坐标系Dxyz，

由于AB＝2，BC＝AA1＝1，所以A1(1，0，1)，B(1，2，0)，C1(0，2，1)，D1(0，0，1)，所以A1C1＝(－1，2，0)，BC1＝(－1，0，1)，D1C1＝(0，2，0)．设平面A1BC1的法向量为n＝(x，y，z)，则有A1C1·n=0，BC1·n=0，即-x+2y=0，-x+z=0，令x＝2，得y＝1，z＝2，则n＝(2，1，2)为平面A1BC1的一个法向量．设D1C1与平面A1BC1所成角为θ，则sin θ＝|cos 〈D1C1，n〉|＝D1C1·nD1C1n＝22×3＝13，即D1C1与平面A1BC1所成角的正弦值为13.
2．(2022·北京卷)如图，在三棱柱ABC­A1B1C1中，侧面BCC1B1为正方形，平面BCC1B1⊥平面ABB1A1，AB＝BC＝2，M，N分别为A1B1，AC的中点．
(1)求证：MN∥平面BCC1B1.
(2)再从条件①、条件②这两个条件中选择一个作为已知，求直线AB与平面BMN所成角的正弦值．
条件①：AB⊥MN；
条件②：BM＝MN.
注：如果选择条件①和条件②分别解答，按第一个解答计分．

(1)证明：取AB中点K，连接NK，MK，
因为M为A1B1的中点．所以B1M∥BK，且B1M∥BK，
所以四边形BKMB1是平行四边形，故MK∥BB1，
MK⊄平面BCC1B1，BB1⊂平面BCC1B1，
所以MK∥平面BCC1B1，
因为K是AB的中点，N是AC的中点，
所以NK∥BC，
因为NK⊄平面BCC1B1，BC⊂平面BCC1B1，
所以NK∥平面BCC1B1，又NK∩MK＝K，
所以平面NMK∥平面BCC1B1，
又MN⊂平面NMK，
所以MN∥平面BCC1B1.
(2)解：因为侧面BCC1B1为正方形，平面BCC1B1⊥平面ABB1A1，平面BCC1B1∩平面ABB1A1＝BB1，
所以CB⊥平面ABB1A1，
所以CB⊥AB，又NK∥BC，
所以AB⊥NK，
若选①：因为AB⊥MN，又MN∩NK＝N，
所以AB⊥平面MNK，
又MK⊂平面MNK，
所以AB⊥MK，又MK∥BB1，
所以AB⊥BB1，
所以BC，BA，BB1两两垂直．
若选②：因为CB⊥平面ABB1A1，NK∥BC，所以NK⊥平面ABB1A1，KM⊂平面ABB1A1，
所以MK⊥NK，又BM＝MN，NK＝12BC，BK＝12AB，
所以△BKM≌△NKM，所以∠BKM＝∠NKM＝90°，
所以AB⊥MK，又MK∥BB1，所以AB⊥BB1，
所以BC，BA，BB1两两垂直．
以B为坐标原点，BC，BA，BB1为坐标轴建立如图所示的空间直角坐标系，

则B(0，0，0)，N(1，1，0)，M(0，1，2)，A(0，2，0)，
所以BM＝(0，1，2)，BN＝(1，1，0)，
设平面BMN的一个法向量为n＝(x，y，z)，
则n·BM=y+2z=0，n·BN=x+y=0，令z＝1，则y＝－2，x＝2，
所以平面BMN的一个法向量为n＝(2，－2，1)，
又BA＝(0，2，0)，
设直线AB与平面BMN所成角为θ，
所以sin θ＝|cos 〈n，BA〉|＝n·BAn·BA＝44+4+1×2＝23.
所以直线AB与平面BMN所成角的正弦值为23.

考点3　求二面角——应用性

考向1　由向量法求二面角的三角函数值
(2022·新高考Ⅱ卷)如图，PO是三棱锥P­ABC的高，PA＝PB，AB⊥AC，E为PB的中点．
(1)证明：OE∥平面PAC；
(2)若∠ABO＝∠CBO＝30°，PO＝3，PA＝5，求二面角C­AE­B的正弦值．

(1)证明：连接OA，OB，依题意，OP⊥平面ABC，
又OA⊂平面ABC，OB⊂平面ABC，则OP⊥OA，OP⊥OB，
所以∠POA＝∠POB＝90°，
又PA＝PB，OP＝OP，则△POA≌△POB，
所以OA＝OB，
延长BO交AC于点F，又AB⊥AC，则在Rt△ABF中，O为BF中点，连接PF，
在△PBF中，O，E分别为BF，BP的中点，则OE∥PF，
因为OE⊄平面PAC，PF⊂平面PAC，
所以OE∥平面PAC．
(2)解：过点A作AM∥OP，以AB，AC，AM分别为x轴、y轴、z轴建立如图所示的空间直角坐标系，

由于PO＝3，PA＝5，由(1)知OA＝OB＝4，
又∠ABO＝∠CBO＝30°，则AB＝43，
所以P(23，2，3)，B(43，0，0)，A(0，0，0)，E33，1，32，
设AC＝t，则C(0，t，0)，
设平面AEB的一个法向量为n＝(x，y，z)，又AB＝(43，0，0)，AE＝33，1，32，
则n·AB=43x=0， n·AE=33x+y+32z=0，则可取n＝(0，3，－2)，
设平面AEC的一个法向量为m＝(a，b，c)，又AC＝(0，t，0)，AE＝33，1，32，
则m·AC=tb=0， m·AE=33a+b+32c=0，则可取m＝(－3，0，6)，
设锐二面角C­AE­B的平面角为θ，则cos θ＝|cos〈m，n〉|＝m·nmn＝4313，
所以sin θ＝1-cos2θ＝1113，即二面角C­AE­B正弦值为1113.

利用空间向量计算二面角大小的常用方法
(1)找法向量：分别求出二面角的两个半平面所在平面的法向量，然后通过两个平面的法向量的夹角得到二面角的大小，但要注意结合实际图形判断所求角的大小．若要求的为两个平面的夹角，只需写出在0，π2范围的一个角即可．
(2)找与棱垂直的方向向量：分别在二面角的两个半平面内找到与棱垂直且以垂足为起点的两个向量，则这两个向量的夹角的大小就是二面角的大小．
考向2　由二面角求几何值或参数值
(2021·新高考Ⅰ卷)如图，在三棱锥A­BCD中，平面ABD⊥平面BCD，AB＝AD，O为BD的中点．
(1)证明：OA⊥CD；
(2)若△OCD是边长为1的等边三角形，点E在棱AD上，DE＝2EA，且二面角E­BC­D的大小为45°，求三棱锥A­BCD的体积．

(1)证明：因为AB＝AD，O为BD的中点，所以OA⊥BD．
因为平面ABD⊥平面BCD，平面ABD∩平面BCD＝BD，OA⊂平面ABD，所以OA⊥平面BCD．
因为CD⊂平面BCD，所以OA⊥CD．
(2)解：以O为坐标原点，OD，OA所在的直线分别为y轴、z轴，过点O且垂直于BD的直线为x轴，建立如图所示的空间直角坐标系．

设OA＝t，则O(0，0，0)，B(0，－1，0)，
C32，12，0，A(0，0，t)，D(0，1，0)，
所以AB＝(0，－1，－t)，BC＝32，32，0，AD＝(0，1，－t)，AE＝13AD＝0，13，-t3，BE＝AE-AB⃗＝0，43，2t3.
易知平面BCD的一个法向量为n＝(0，0，1)．
设平面BCE的一个法向量为m＝(x，y，z)，则m·BC=0，m·BE=0，即32x+32y=0，43y+2t3z=0.
不妨取x＝3，则y＝－1，z＝2t，即m＝3，-1，2t.
因为二面角E­BC­D的大小为45°，所以|cos 〈n，m〉|＝n·mnm＝2t4+4t2＝22，解得t＝1(负值已舍去)．
由OB＝OC＝OD＝1，得BC⊥CD，所以BC＝3，
所以三棱锥A­BCD的体积为13×12×1×3×1＝36.

在已知二面角的条件下求几何量或参数的值时，注意用好二面角的定义，求出相关的量，或由此写出相关点的坐标，为用向量法求解问题做好必要的条件准备．

如图，AB为圆O的直径，点E，F在圆O上，AB∥EF，矩形ABCD和圆O所在的平面互相垂直，已知AB＝2，EF＝1.
(1)求证：平面DAF⊥平面CBF；
(2)当AD的长为何值时，二面角D­FC­B的平面角的大小为60°？

(1)证明：因为平面ABCD⊥平面ABEF，CB⊥AB，平面ABEF∩平面ABCD＝AB，CB⊂平面ABCD，所以CB⊥平面ABEF.因为AF⊂平面ABEF，所以CB⊥AF.
又因为AB为圆的直径，所以FB⊥AF.又CB∩BF＝B，所以AF⊥平面CBF.
因为AF⊂平面DAF，所以平面DAF⊥平面CBF.
(2)解：设EF，CD的中点分别为G，H，以O为坐标原点，建立空间直角坐标系(如图)，设AD＝t，

则D(1，0，t)，C(－1，0，t)，A(1，0，0)，B(－1，0，0)，F12，32，0，所以CD＝(2，0，0)，FD＝12，-32，t.
设平面DCF的法向量为n1＝(x，y，z)，则n1·CD＝0，n1·FD＝0，即2x=0， 12x-32y+tz=0，取z＝3，则n1＝(0，2t，3)．
由(1)可知AF⊥平面CBF，取平面CBF的一个法向量n2＝AF＝-12，32，0，
所以cos 60°＝3t4t2+3，解得t＝64，所以线段AD的长为64时，二面角D­FC­B的平面角的大小为60°.

考点4　求空间距离问题——综合性

(1)已知直三棱柱ABC­A1B1C1中，AA1＝1，AB＝4，BC＝3，∠ABC＝90°，则点B到直线A1C1的距离为________．
135　解析：以B为原点，建立如图所示的空间直角坐标系，

则A1(4，0，1)，C1(0，3，1)，所以直线A1C1的方向向量为A1C1＝(－4，3，0)，而BC1＝(0，3，1)，所以点B到直线A1C1的距离
d＝BC12-BC1·A1C1A1C12＝10-952＝135.
(2)如图，已知正方形ABCD的边长为1，PD⊥平面ABCD，且PD＝1，E，F分别为AB，BC的中点．
①求点D到平面PEF的距离；
②求直线AC到平面PEF的距离．

解：①以D为坐标原点，DA，DC，DP所在的直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系，

则D(0，0，0)，P(0，0，1)，A(1，0，0)，C(0，1，0)，E1，12，0，F12，1，0，
则PE＝1，12，-1，PF＝12，1，-1.
设平面PEF的法向量为n＝(x，y，z)，
则n·PE=0，n·PF=0，
所以x+12y-z=0，12x+y-z=0，即z=32y，x=y.
令y＝2，则n＝(2，2，3)．又DP＝(0，0，1)，
所以点D到平面PEF的距离
d＝DP·nn＝317＝31717.
②由于E，F分别是AB，BC的中点，所以EF∥AC．
因为AC⊄平面PEF，所以AC∥平面PEF，所以点A到平面PEF的距离即为直线AC到平面PEF的距离．
由于AE＝0，12，0，又由①知平面PEF的法向量为n＝(2，2，3)，
所以点A到平面PEF的距离d＝AE·nn＝117＝1717，即直线AC到平面PEF的距离为1717.

1．空间距离包括空间内任意两点之间的距离、点到平面的距离、直线与平面的距离以及两平行平面之间的距离，其中两点间的距离可以用向量的模长处理，其他三种距离的求解都可以转化为点到平面的距离．
2．用向量法求点面距的步骤：

(1)建系：建立恰当的空间直角坐标系．
(2)求点坐标：写出(求出)相关点的坐标．
(3)求向量：求出相关向量的坐标(AP，α内两不共线向量，平面α的法向量n)．
(4)求距离d＝AP·nn.

1．在空间直角坐标系Oxyz中，四面体ABCD的顶点坐标分别是A(0，0，2)，B(2，2，0)，C(1，2，1)，D(2，2，2)，则点B到平面ACD的距离是(　　)
A．233 B．33
C．223 D．23
A　解析：由题意知AD＝(2，2，0)，CD＝(1，0，1)，BD＝(0，0，2)，设平面ACD的法向量为n＝(x，y，z)，则n·AD=2x+2y=0，n·CD=x+z=0， 取x＝1，则n＝(1，－1，－1)，所以BD·nn＝-23＝233，即点B到平面ACD的距离是233.故选A．
2．若正方体ABCD­A1B1C1D1的棱长为a，则平面AB1D1与平面BDC1的距离为(　　)
A．2a B．3a
C．23a D．33a
D　解析：建立空间直角坐标系如图．

则A(a，0，0)，D(0，0，0)，C1(0，a，a)，D1(0，0，a)，B1(a，a，a)，
设n＝(x，y，z)为平面AB1D1的法向量，
则n·AB1=ay+z=0， n·AD1=a-x+z=0，得y=-z，x=z. 取z＝1，则n＝(1，－1，1)为平面AB1D1的一个法向量．
又因为AD1∥BC1，AB1∥DC1，AD1∩AB1＝A，
DC1∩BC1＝C1，所以平面AB1D1∥平面BDC1.
所以平面AB1D1与平面BDC1的距离可转化为点C1到平面AB1D1的距离d.
因为C1B1＝(a，0，0)，平面AB1D1的法向量为n＝(1，－1，1)，
所以d＝C1B1·nn＝a3＝33a.


如图，在四棱锥S-ABCD中，AB∥CD，BC⊥CD，侧面SAB为等边三角形，AB＝BC＝2，CD＝SD＝1.
(1)证明：SD⊥平面SAB；
(2)求AB与平面SBC所成角的正弦值的大小．

[四字程序]
读
想
算
思
AB∥CD，
BC⊥CD，
△SAB为等边三角形，
AB＝BC＝2，CD＝SD＝1
定义法，借助点到平面的距离，法向量
勾股定理、余弦定理、法向量求解
多方法、多角度对立体几何知识的掌握及空间向量在解决立体几何中的应用



思路参考：利用定义寻找线面角的位置直接求解．
(1)证明：取AB的中点为点E，连接DE，则四边形BCDE为矩形，DE＝BC＝2.
连接SE，则SE⊥AB，SE＝3.
又SD＝1，故DE2＝SE2＋SD2，所以∠DSE为直角．由AB⊥DE，AB⊥SE，DE∩SE＝E，
得AB⊥平面SDE，
所以AB⊥SD，SD与两条相交直线AB，SE都垂直，所以SD⊥平面SAB．
(2)解：因为CD∥AB，所以CD与平面SBC所成的角即为AB与平面SBC所成的角．如图，取SC的中点M，连接BM，DM.

因为DS＝DC，BS＝BC，所以SC⊥DM，SC⊥BM.因为DM∩BM＝M，所以SC⊥平面BDM，
所以平面BDM⊥平面SBC．
作DN⊥BM，垂足为点N，则DN⊥平面SBC．因为DM∩BM＝M，连接CN.
CN为CD在平面SBC上的射影，∠DCN即为CD与平面SBC所成的角．
因为SD⊥AB，CD∥AB，
所以SD⊥CD，所以|SC|＝SD2+CD2＝2，
|BM|＝BC2-CM2＝22-222＝142，
cos ∠DBM＝BD2+BM2-DM22BD·BM
＝52+1422-2222×5×142＝870，
sin ∠DBM＝670，DN＝5×670＝217，
sin ∠DCN＝DNCD＝2171＝217.
所以AB与平面SBC所成角的正弦值为217.

思路参考：借助点到平面的距离间接求解．
(1)证明：同解法1.
(2)解：VA-SBC＝VS-ABC，
过点S作SF⊥DE，则SF⊥平面ABCD．
|SF|＝SD·SEED＝32.
VS-ABC＝13S△ABC·|SF|
＝13×12|AB|·|BC|·|SF|
＝13×12×2×2×32＝33.
设A到平面SBC的距离为h，取SC中点M，连接BM.

因为SD⊥AB，CD∥AB，SD⊥CD，|SC|＝SD2+CD2＝2，
|BM|＝BC2-CM2＝22-222＝142，
VA-SBC＝13S△SBC·h
＝13×12|SC|·|BM|·h
＝13×12×2×142×h＝76h.
因为76h＝33， 所以h＝33×67＝2217，
即A到平面SBC的距离为2217.
又因为AB＝2，设AB与平面SBC所成的角为α，
则sin α＝hAB＝22172＝217，
所以AB与平面SBC所成角的正弦值为217.

思路参考：建立空间直角坐标系，利用法向量求解．
(1)证明：同解法1.
(2)解：如图，以C为坐标原点，CD，CB所在直线分别为x轴、y轴建立如图所示的空间直角坐标系，

则D(1，0，0)，A(2，2，0)，B(0，2，0)．
因为平面SDE⊥平面ABCD，
CD＝1，DF＝12，SF＝32，所以S1，12，32.
设平面SBC的法向量为n＝(x，y，z)，
BS＝1，-32，32，CB＝(0，2，0)，
故x-32y+32z=0，2y=0， 取z＝2，得x＝－3，y＝0，所以平面SBC的一个法向量为n＝(－3，0，2)．
又AB＝(－2，0，0)，所以|cos〈AB，n〉|＝AB·nABn＝217.
故AB与平面SBC所成角的正弦值为217.

思路参考：变换建系的方法，空间直角坐标系中各点坐标会发生变化，但求角的方法是不变的．
(1)证明：同解法1.
(2)解：如图，以D为坐标原点，射线DE为x轴正半轴，射线DC为y轴正半轴，建立如图所示的空间直角坐标系，

则D(0，0，0)，A(2，－1，0)，B(2，1，0)，C(0，1，0)．
因为平面SDE⊥平面ABCD，点S在xOz平面内，DF＝12，SF＝32，所以S12，0，32.
设平面SBC的法向量为n＝(x，y，z)，
BS＝-32，-1，32，CB＝(2，0，0)，
故-32x-y+32z=0，2x=0. 取z＝2，得x＝0，y＝3.
所以平面SBC的一个法向量为n＝(0，3，2)．
又AB＝(0，2，0)，
所以|cos〈AB，n〉|＝AB·nABn＝232×7＝217.
故AB与平面SBC所成角的正弦值为217.

1．本题考查线面角的运算，解法灵活，基本解题策略一种是利用定义寻找线面角，然后通过解三角形计算，另一种是建立空间直角坐标系，通过法向量与方向向量夹角处理．
2．基于课程标准，解答本题需要熟练掌握线面角的寻找以及空间向量求线面角的方法，具有良好的运算求解能力、空间想象能力．本题的解答过程体现了数学探索的魅力．
3．基于高考数学评价体系，解答本题的过程中，通过不同的思路引导，将求线面角转化为最基本的数学模型，体现了基础性；解题过程中知识的转化，体现了综合性．

如图1，四边形ABCD为菱形，且∠A＝60°，AB＝2，E为边AB的中点．现将四边形EBCD沿DE折起至EBHD，如图2.若二面角A-DE-H的大小为60°，求平面ABH与平面ADE夹角的余弦值．
　　
图1　　　　　　　　　图2
解：(方法一)分别取AE，AD的中点O，K，连接OK，OB．由DE⊥平面ABE，可知∠AEB为二面角A-DE-H的平面角，即有∠AEB＝60°.
因为O为AE的中点，所以BO⊥AE.因为BO⊥DE，所以BO⊥平面ADE，则以点O为坐标原点，分别以直线KO，OE，OB为x轴、y轴、z轴建立空间直角坐标系．

由条件，易得A(0，－12，0)，B0，0，32，D-3，12，0，E0，12，0.
再设H(x0，y0，z0)，而ED＝(－3，0，0)，
DH＝x0+3，y0-12 ，z0.
由ED⊥DH，得ED·DH＝0，得x0＝－3.
由HB=2，HD=2，
可得x02+y02+z0-322=4， x0+32+y0-122+z02=4.
将x0＝－3代入，可得y0＝－12，z0＝3，即H-3，-12，3，则BH＝-3，-12，32，AH＝(－3，0，3).
设平面ABH法向量为n1＝(x1，y1，z1)，
则-3x1+3z1=0， -3x1-12 y1+32z1=0，
即y1=-3x1，z1=x1.
令x1＝1，得y1＝－3，z1＝1，即n1＝(1，－3，1)．
而平面ADE的一个法向量为n2＝(0，0，1)．
于是平面ABH与平面ADE的夹角θ的余弦值为cos θ＝n1·n2n1n2＝11×5＝55.
(方法二)延长HB，DE交于点L，连接AL，取AE的中点O，过点O作OM⊥AL于点M，连接MB，如图．

由DE⊥平面ABE，可知∠AEB为二面角A-DE-H的一个平面角，即有∠AEB＝60°.
因为O为AE的中点，所以BO⊥AE.
因为BO⊥DE，所以BO⊥平面ADE，即BO⊥AL且BO⊥MO.
又因为OM⊥AL，所以AL⊥平面BOM，即∠BMO为平面ADE与平面ABH的夹角的一个平面角．
而BO＝32，AO＝12.易得LE＝3，而AE＝1，∠AEL＝90°，所以∠EAL＝60°，则MO＝34.
由勾股定理，得MB＝322+342＝154，
则cos ∠BMO＝MOMB＝55，
即平面ADE与平面ABH的夹角的余弦值为55.
(方法三)延长HB，DE交于点L，连接AL，过点D作DQ∥AE且与LA的延长线交于点Q，连接QH.分别取DQ，AE中点M，O，连接AM，BO.再取MD中点O′，连接OO′.
因为QD∥AE，HD∥BE且QD，HD为平面HDQ内两条相交直线，AE，BE为平面ABE内两条相交直线，所以平面HDQ∥平面ABE.
因为DE⊥平面ABE，所以DE⊥平面HDQ，
即∠HDQ为二面角A-DE-H的一个平面角，即有∠HDQ＝60°.
由HD＝2，得HM＝3，MD＝1，则MO′＝12.
因为M为QD中点，所以HM⊥QD．
因为HM⊥DE，所以MH⊥平面ADE.
以点O为坐标原点，分别以直线O′O，OE，OB为x，y，z轴建立空间直角坐标系，如图．

易得A0，-12，0，B0，0，32，H-3，-12，3，
则有AB＝0，12，32，BH＝-3，-12，32.
设平面ABH的一个法向量为n1＝(x1，y1，z1)，
则12y1+32z1=0， -3x1-12 y1+32z1=0，
即y1=-3z1，z1=x1.
令x1＝1，得y1＝－3，z1＝1，
即n1＝(1，－3，1)．
而平面ADE的一个法向量为n2＝(0，0，1)．
于是平面ABH与平面ADE的夹角θ的余弦值为cos θ＝n1·n2n1n2＝11×5＝55.
课时质量评价(三十八)
A组　全考点巩固练
1．在三棱锥A­BCD中，平面ABD与平面BCD的法向量分别为n1，n2.若〈n1，n2〉＝π3，则二面角A­BD­C的大小为(　　)
A．π3 B．2π3
C．π3或2π3 D．π6或π3
C　解析：因为二面角的范围是[0，π]，且〈n1，n2〉＝π3，所以二面角A­BD­C的大小为π3或2π3.故选C．
2．如图，点A，B，C分别在空间直角坐标系Oxyz的三条坐标轴上，OC＝(0，0，2)，平面ABC的法向量为n＝(2，1，2)，设二面角C­AB­O的大小为θ，则cos θ等于(　　)

A．43 B．53
C．23 D．－23
C　解析：由题意可知，平面ABO的一个法向量为OC＝(0, 0, 2)，由图可知，二面角C­AB­O为锐角，由空间向量的结论可知，cos θ＝OC·nOCn＝42×3＝23.
3．如图，在长方体ABCD­A1B1C1D1中，AD＝AA1＝1，AB＝3，E为线段AB上一点，且AE＝13AB，则DC1与平面D1EC所成角的正弦值为(　　)

A．33535 B． 277
C．33 D．24
A　解析：如图，以D为坐标原点，DA，DC，DD1所在直线分别为x轴、y轴、z轴建立空间直角坐标系，

则C1(0，3，1)，D1(0，0，1)，E(1，1，0)，C(0，3，0)，所以DC1＝(0，3，1)，D1E＝(1，1，－1)，D1C＝(0，3，－1)．设平面D1EC的法向量为n＝(x，y，z)，则n·D1E=0，n·D1C=0，即x+y-z=0，3y-z=0， 取y＝1，得n＝(2，1，3)．所以cos 〈DC1，n〉＝DC1·nDC1n＝33535，所以DC1与平面D1EC所成的角的正弦值为33535.
4．在正方体ABCD­A1B1C1D1中，点E为BB1的中点，则平面A1ED与平面ABCD所成的锐二面角的余弦值为(　　)
A．12 B．23
C．33 D．22
B　解析：以A为坐标原点建立如图所示的空间直角坐标系Axyz，

设棱长为1，则A1(0，0，1)，E1，0，12，D(0，1，0)，所以A1D＝(0，1，－1)，A1E＝1，0，-12，设平面A1ED的一个法向量为n1＝(1，y，z)，则n1·A1D=0，n1·A1E=0，即y-z=0，1-12z=0，所以y=2，z=2，所以n1＝(1，2，2)．又平面ABCD的一个法向量为n2＝(0，0，1)，所以cos 〈n1，n2〉＝23×1＝23.即平面A1ED与平面ABCD所成的锐二面角的余弦值为23.
5．在直三棱柱ABC­A1B1C1中，AA1＝2，二面角B­AA1­C1的大小为60°，点B到平面ACC1A1的距离为3，点C到平面ABB1A1的距离为23，则直线BC1与直线AB1所成角的正切值为(　　)
A．7 B．6
C．5　 D．2
A　解析：由题意可知，∠BAC＝60°，点B到平面ACC1A1的距离为3，点C到平面ABB1A1的距离为23，所以在三角形ABC中，AB＝2，AC＝4，BC＝23，∠ABC＝90°，则AB1·BC1＝(BB1-BA)·(BB1+BC1)＝4，
|AB1|＝22，|BC1|＝4，cos 〈AB1，BC1〉＝AB1·BC1AB1BC1＝24，故tan 〈AB1，BC1〉＝7.
6．(多选题)设三棱锥V­ABC的底面是正三角形，侧棱长均相等，P是棱VA上的点(不含端点)．记直线PB与直线AC所成的角为α，直线PB与平面ABC所成的角为β，二面角P­AC­B的平面角为γ，则α，β，γ大小关系正确的是(　　)
A．α＞β B．α＝β
C．γ＞β D．γ≥β
AC　解析：过点B作直线l∥AC，过点P作底面ABC的垂线PD，D为垂足，过点D作DF⊥AB于点F，作DE⊥l于点E，连接AD，BD，PF，PE.

由题意可知，二面角P­AC­B的大小与二面角P­AB­C的大小相等，结合空间角的定义知∠PBE＝α，∠PBD＝β，∠PFD＝γ，在Rt△PEB与Rt△PDB中，由PE＞PD得sin α＞sin β，所以α＞β(α，β均为锐角)．故A正确，B错误；在Rt△PDB与Rt△PDF中，由PB＞PF得sin β＜sin γ，所以γ＞β(β，γ均为锐角)．故C正确；由于不存在PB＝PF的可能，故D错误．
7．如图，在正方形ABCD中，EF∥AB．若沿EF将正方形折成一个二面角后，AE∶ED∶AD＝1∶1∶2，则AF与CE所成角的余弦值为________．
→
45　解析：因为AE∶ED∶AD＝1∶1∶2，所以AE⊥ED，即AE，DE，EF两两垂直，所以建立如图所示的空间直角坐标系．

设AB＝EF＝CD＝2，则E(0，0，0)，A(1，0，0)，F(0，2，0)，C(0，2，1)，所以AF＝(－1，2，0)，EC＝(0，2，1)，所以cos 〈AF，EC〉＝AF·ECAFEC＝45×5＝45，所以AF与CE所成角的余弦值为45.
8．正四棱锥P­ABCD，底面四边形ABCD是边长为2的正方形，PA＝5，其内切球为球G，平面α过AD与棱PB，PC分别交于点M，N，且与平面ABCD所成二面角为30°，则平面α截球G所得的图形的面积为________．
π3　解：如图建立空间直角坐标系，则A(0，0，0)，D(2，0，0)，B(0，2，0)，C(2，2，0)．因为PA＝PD＝PB＝PC＝5，AO＝12AC＝2.所以PO＝PA2-AO2＝3，所以P(1，1，3)，O(1，1，0)，则内切球的球心G在PO上，设G(1，1，h)，内切球的半径为R，S△PAD＝S△PCD＝S△PBC＝S△PAB＝12×2×52-12＝2.由等体积法可得13R(2＋2＋2＋2＋2×2)＝13×2×2×3，解得R＝33，则G1，1，33.因为平面α过AD，设平面α的法向量为n＝(0，－1，a)，平面ABCD的法向量为m＝(0，0，1)，设平面α与平面ABCD所成二面角为30°，则cos 30°＝n·mnm＝32，即aa2+1＝32，解得a＝3或a＝－3(舍去)，所以n＝(0，－1，3)，则圆心G到平面α的距离d＝AG·nn＝1×-1+3×332＝0，所以截球G所得图形的面积为πR2＝π3.

9．(2022·泰安一模)如图，在五面体ABCDE中，已知AC⊥平面BCD，ED∥AC，且AC＝BC＝2ED＝2，DC＝DB＝3.
(1)求证：平面ABE⊥平面ABC；
(2)求二面角A­BE­C的余弦值．

(1)证明：取BC中点M，AB中点N，连接DM，MN，EN.
所以MN∥AC且MN＝12AC，
又DE＝12AC，DE∥AC，所以DE∥MN，且DE＝MN，
所以四边形MNED是平行四边形，
所以EN∥DM且EN＝DM，
又AC⊥平面BCD，AC⊂平面ABC，所以平面ABC⊥平面BCD，
因为DC＝DB，所以DM⊥BC，
又平面ABC∩平面BCD＝BC，DM⊂平面BCD，
所以DM⊥平面ABC，所以EN⊥平面ABC，
又EN⊂平面ABE，所以平面ABE⊥平面ABC．
(2)解：由(1)知，AC⊥BC，EN∥DM且EN＝DM，EN⊥平面ABC，平面ABE⊥平面ABC，
以C为原点，CA，CB所在直线为x，y轴，以过点C，与MD平行的直线为z轴，建立如图所示的空间直角坐标系，
则A(2，0，0)，B(0，2，0)，N(1，1，0)，E(1，1，2)，
则CB＝(0，2，0)，CN＝(1，1，0)，CE＝(1，1，2)，
设平面BCE的法向量为n＝(x，y，z)，
则n·CE=x+y+2z=0，n·CB=2y=0， 取z＝2，则x=-2，y=0，所以n＝(－2，0，2)为平面BCE的一个法向量，
又AC＝BC，则CN⊥AB，
又平面ABC∩平面ABE＝AB，CN⊂平面ABC，
所以CN⊥平面ABE，即CN＝(1，1，0)为平面ABE的一个法向量，
所以cos 〈n，CN〉＝n·CNn·CN＝-22·6＝33，
显然二面角A­BE­C为锐角，故其余弦值为33.

B组　新高考培优练
10．(2022·浙江卷)如图，已知ABCD和CDEF都是直角梯形，AB∥DC，DC∥EF，AB＝5，DC＝3，EF＝1，∠BAD＝∠CDE＝60°，二面角F­DC­B的平面角为60°.设M，N分别为AE，BC的中点．
(1)求证：FN⊥AD；
(2)求直线BM与平面ADE所成角的正弦值.

(1)证明：由于CD⊥CB，CD⊥CF，
平面ABCD∩平面CDEF＝CD，CF⊂平面CDEF，CB⊂平面ABCD，
所以∠FCB为二面角F­DC­B的平面角，
则∠FCB＝60°.
又CF＝3(CD－EF)＝23，CB＝3(AB－CD)＝23，
则△BCF是等边三角形，则CB⊥FN，
因为DC⊥FC，DC⊥BC，FC∩BC＝C，FC⊂平面FCB，BC⊂平面FCB，
所以DC⊥平面FCB，因为FN⊂平面FCB，所以DC⊥FN，
又因为DC∩CB＝C，DC⊂平面ABCD，CB⊂平面ABCD，
所以FN⊥平面ABCD，因为AD⊂平面ABCD，故FN⊥AD．
(2)解：由于FN⊥平面ABCD，如图建系：

于是B(0，3，0)，A(5，3，0)，F(0，0，3)，
E(1，0，3)，D(3，－3，0)，则M3，32，32，
BM＝3，-32，32，DA＝(2，23，0)，DE＝(－2，3，3)，
设平面ADE的法向量n＝(x，y，z)，
则n·DA=0，n·DE=0，所以2x+23y=0， -2x+3y+3z=0，
令x＝3，则y＝－1，z＝3，
所以平面ADE的法向量n＝(3，－1，3)，
设BM与平面ADE所成角为θ，
则sin θ＝BM·nBMn＝5714.
11．如图，四边形ABCD是矩形，PA⊥平面ABCD，DE⊥平面ABCD，AB＝DE＝1，AD＝PA＝2，点F在棱PA上．
(1)求证：BF∥平面CDE；
(2)求二面角C­PE­A的余弦值；
(3)若点F到平面PCE的距离为13，求线段AF的长．

(1)证明：因为PA⊥平面ABCD，DE⊥平面ABCD，
所以PA∥DE，又PA⊄平面CDE，DE⊂平面CDE，
所以PA∥平面CDE，又四边形ABCD是矩形，
所以AB∥CD，又AB⊄平面CDE，CD⊂平面CDE，
所以AB∥平面CDE，结合PA∥平面CDE，
又AB，PA⊂平面PAB，AB∩PA＝A，
所以平面PAB∥平面CDE，又点F在棱PA上，所以BF⊂平面PAB，
所以BF∥平面CDE.
(2)解：以A为原点，分别以AB，AD，AP所在直线为x轴、y轴、z轴建立如图所示的空间直角坐标系，
由题意有A(0，0，0)，P(0，0，2)，C(1，2，0)，
E(0，2，1)，所以PC＝(1，2，－2)，PE＝(0，2，－1)，
易知平面APE的一个法向量为m＝(1，0，0)，
设平面CPE的法向量n＝(x，y，z)，
则n·PC=x+2y-2z=0，n·PE=2y-z=0，
令y＝1，则z＝2，x＝2,
所以n＝(2，1，2)，由图知二面角C­PE­A的平面角θ为锐角，
所以cos θ＝|cos 〈n，m〉|＝n·mnm＝23，
所以二面角C­PE­A的余弦值为23.

(3)解：连接BD，设点F(0，0，t)，0≤t≤2，则FP＝(0，0，2－t)，
又由(2)中平面CPE的法向量n＝(2，1，2)，
所以F到平面PCE的距离为d＝FP·nn＝4-2t3＝13，
所以t＝32，即AF＝32.
12．如图，已知△ABC是以AC为底边的等腰三角形，将△ABC绕AB转动到△PAB位置，使得平面PAB⊥平面ABC，连接PC，E，F分别是PA，CA的中点．
(1)证明：EF⊥AB；
(2)在①S△ABC＝33，②点P到平面ABC的距离为3，③直线PB与平面ABC所成的角为60°这三个条件中选择两个作为已知条件，求二面角E­BF­A的余弦值．

(1)证明：如图(1)，过点E作ED⊥AB，垂足为D，连接DF.由题意知，△PAB≌△CAB，易证△EDA≌△FDA，
所以∠EDA＝∠FDA＝π2，即FD⊥AB．
因为ED⊥AB，ED∩FD＝D，所以AB⊥平面EFD．
又因为EF⊂平面EFD，所以EF⊥AB．

图(1)
(2)解：过点P作PO⊥AB，垂足为O，连接CO，则CO⊥AB．因为平面PAB⊥平面ABC，所以PO⊥平面ABC．以O为坐标原点，以OA，OC，OP所在直线分别为x轴、y轴、z轴建立如图(2)所示的空间直角坐标系．

图(2)
设AB＝a，∠ABC＝θ，
由条件①得S△ABC＝12a2sin θ＝33，由条件②得PO＝a sin θ＝3，由条件③得∠PBO＝60°，即θ＝120°.
若选条件①②，可求得a＝23，B(3，0，0)，A(33，0，0)，P(0，0，3)，C(0，3，0)．
因为E332，0，32，F332，32，0，所以BF＝32，32，0，BE＝32，0，32.
设平面BEF的一个法向量m＝(x，y，z)，由m·BF=0，m·BE=0，得32x+32y=0，32x+32z=0，取m＝(－3，1，1)，
又易知平面BFA的一个法向量n＝(0，0，1)，
故cos〈m，n〉＝m·nmn＝15＝55，
所以二面角E­BF­A的余弦值为55.
若选①③或②③均可求得a＝23，下同．
13．请从下面三个条件中任选一个，补充在下面的横线上，并作答．
①AB⊥BC，②FC与平面ABCD所成的角为π6，③∠ABC＝π3.
如图，在四棱锥P-ABCD中，底面ABCD是菱形，PA⊥平面ABCD，且PA＝AB＝2，PD的中点为F.
(1)在线面AB上是否存在一点G，使得AF∥平面PCG？若存在，指出G在AB上的位置并给以证明；若不存在，请说明理由．
(2)若________，求二面角F-AC-D的余弦值．

解：(1)在线段AB上存在点G，使得AF∥平面PCG，且G为AB的中点．
证明如下：设PC的中点为H，连接FH，GH，如图．

易证四边形AGHF为平行四边形，
则AF∥GH.
又GH⊂平面PCG，AF⊄平面PGC，
所以AF∥平面PGC．
(2)选择①.
因为PA⊥平面ABCD，
所以PA⊥AB，PA⊥AD．
由题意可知，AB，AD，AP两两垂直，
故以A为坐标原点，AB，AD，AP的方向分别为x，y，z轴的正方向建立如图所示的空间直角坐标系．

因为PA＝AB＝2，
所以A(0，0，0)，C(2，2，0)，D(0，2，0)，P(0，0，2)，F(0，1，1)，
所以AF＝(0，1，1)，CF＝(－2，－1，1)．
设平面FAC的法向量为u＝(x，y，z)，则u·AF=0，u·CF=0，即y+z=0， -2x-y+z=0.令y＝1，则x＝－1，z＝－1，则u＝(－1，1，－1)．
易知平面ACD的一个法向量为v＝(0，0，2)，
设二面角F-AC-D的平面角为θ，则cos θ＝u·vuv＝33，即二面角F-AC-D的余弦值为33.
选择②.
设BC中点E，连接AE，取AD的中点M，连接FM，CM，则FM∥PA，且FM＝1.
因为PA⊥平面ABCD，
所以FM⊥平面ABCD，FC与平面ABCD所成的角为∠FCM，
故∠FCM＝π6.
在直角三角形FCM中，CM＝3.又因为CM＝AE，所以AE2＋BE2＝AB2，
所以BC⊥AE，所以AE，AD，AP两两垂直．
故以A为坐标原点，AE，AD，AP的方向分别为x，y，z轴的正方向建立如图所示的空间直角坐标系．

因为PA＝AB＝2，
所以A(0，0，0)，C(3，1，0)，D(0，2，0)，P(0，0，2)，F(0，1，1)，所以AF＝(0，1，1)，CF＝(－3，0，1)．
设平面FAC的法向量为u＝(x，y，z)，则u·AF=0，u·CF=0，
即y+z=0， -3x+z=0.
令x＝3，则y＝－3，z＝3，则u＝(3，－3，3)．
易知平面ACD的一个法向量为v＝(0，0，2)．
设二面角F-AC-D的平面角为θ，则cos θ＝u·vuv＝217，
即二面角F-AC-D的余弦值为217.
选择③.
因为PA⊥平面ABCD，
所以PA⊥BC．
取BC中点E，连接AE.
因为底面ABCD是菱形，∠ABC＝π3，
所以△ABC是正三角形．
又E是BC的中点，所以BC⊥AE，
所以AE，AD，AP两两垂直．
故以A为坐标原点，AE，AD，AP的方向分别为x，y，z轴的正方向建立如图所示的空间直角坐标系．

因为PA＝AB＝2，
所以A(0，0，0)，C(3，1，0)，D(0，2，0)，P(0，0，2)，F(0，1，1)，所以AF＝(0，1，1)，CF＝(－3，0，1)．
设平面FAC的法向量为u＝(x，y，z)，
则u·AF=0，u·CF=0，
即y+z=0， -3x+z=0.令x＝3，
则y＝－3，z＝3，则u＝(3，－3，3)．
易知平面ACD的一个法向量为v＝(0，0，2)，
设二面角F-AC-D的平面角为θ，则cos θ＝u·vuv＝217，即二面角F-AC-D的余弦值为217.