华师版·河南省鹤壁市淇滨中学2022-2023学年八上期中数学试卷

这是一份华师版·河南省鹤壁市淇滨中学2022-2023学年八上期中数学试卷，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2022～2023学年上期淇滨中学八年级上期期中考试
数学试卷
一、选择题（每小题3分，共30分）
1. 下列实数中，是无理数的是（ ）
A B. C. D.
2. 下列运算正确的是（ ）
A B.
C. D.
3. 下列命题中，假命题（　　）
A. 线段垂直平分线上的点到线段两端的距离相等
B. 等腰三角形的两底角相等
C. 面积相等的两个三角形全等
D. 有一个角是的等腰三角形是等边三角形
4. 多项式的公因式是（　　）
A. B. C. D.
5. 如果多项式 x2 + mx + 4 恰好是某个整式的平方，那么 m 的值为（ ）
A. 2 B. －2 C. ±2 D. ±4
6. 等腰三角形两边为a，b，且满足，那么它的周长为（　　）
A. 12 B. 15 C. 12或15 D. 13
7. 如图，，那么添加下列一个条件后，仍无法判定的是（　　）

A. B.
C D.
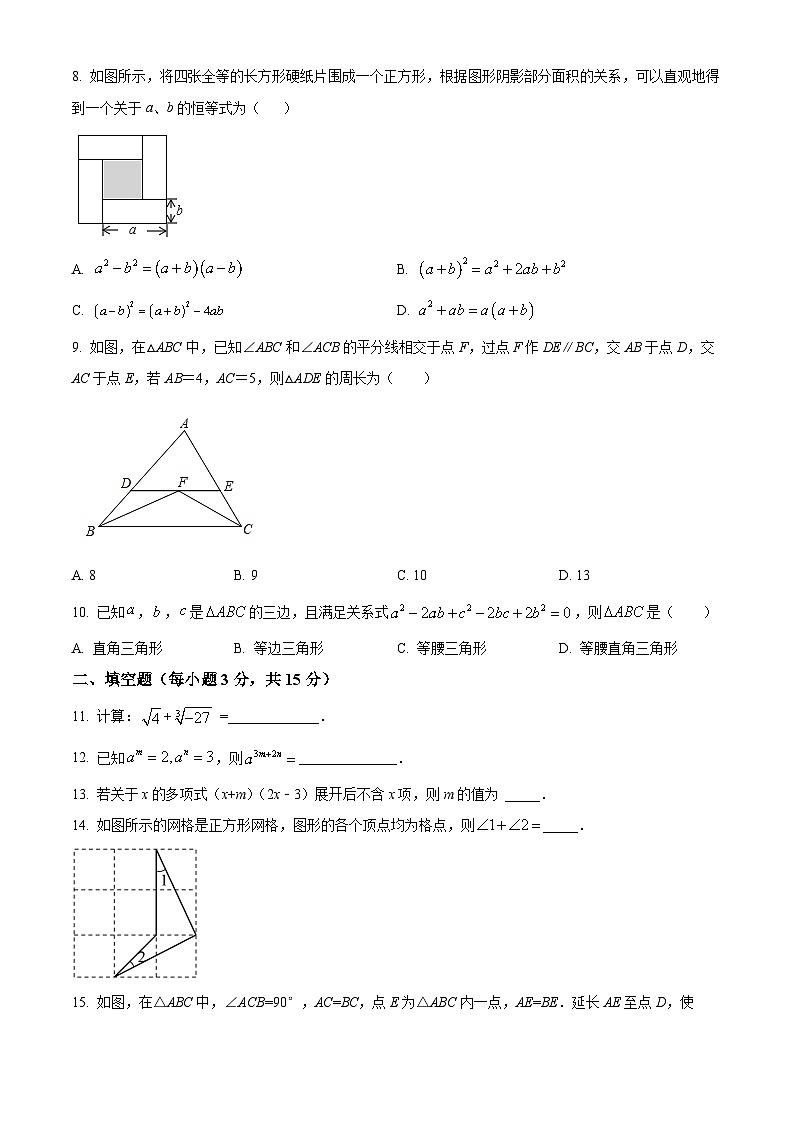
8. 如图所示，将四张全等的长方形硬纸片围成一个正方形，根据图形阴影部分面积的关系，可以直观地得到一个关于a、b的恒等式为（ ）

A. B.
C. D.
9. 如图，在△ABC中，已知∠ABC和∠ACB的平分线相交于点F，过点F作DE∥BC，交AB于点D，交AC于点E，若AB＝4，AC＝5，则△ADE的周长为（　　）

A. 8 B. 9 C. 10 D. 13
10. 已知，，是的三边，且满足关系式，则是（ ）
A. 直角三角形 B. 等边三角形 C. 等腰三角形 D. 等腰直角三角形
二、填空题（每小题3分，共15分）
11. 计算：+ =_____________．
12. 已知，则______________．
13. 若关于x的多项式（x+m）（2x﹣3）展开后不含x项，则m的值为 _____．
14. 如图所示的网格是正方形网格，图形的各个顶点均为格点，则_____．

15. 如图，在△ABC中，∠ACB=90°，AC=BC，点E为△ABC内一点，AE=BE．延长AE至点D，使DE=AC，连接CD，CE．若CD=DE，则∠D的度数是____________．

三、解答题
16. 计算：
（1）
（2）



17. 把下列多项式分解因式：
（1）
（2）





18. 先化简，再求值，其中，，．







19. 如图，数轴上点B，C关于点A成中心对称，若点A表示的数是1，点B表示的数是．

（1）填空：点C表示的数为___________；
（2）点C表示的数为a，a的小数部分为b，求的值．





20. 下面是某同学对多项式进行因式分解的过程．
解：设
原式（第一步）
（第二步）
（第三步）
（第四步）
回答下列问题：
（1）该同学第二步到第三步运用了因式分解的___________．
A．提取公因式 B．平方差公式 C．完全平方公式
（2）请你模仿以上方法尝试对多项式进行因式分解．







21. 问题原型：

（1）如图1，在锐角中，，于点D，在AD上取点E；连接BE，使．求证：．
问题拓展：
（2）如图2，在问题原型的条件下，F为BC的中点，连接EF并延长至点M，使，连接CM、AM，则为___________三角形．




22. 如图，将一张大长方形纸板按图中虚线裁剪成9块，其中有2块是边长为a厘米的大正方形，2块是边长都为b厘米的小正方形，5块是长为a厘米，宽为b厘米的相同的小长方形，且．
（1）观察图形，可以发现代数式可以因式分解为______．
（2）若图中阴影部分的面积为20平方厘米，大长方形纸板的周长为24厘米，求图中空白部分的面积．






23. 如图，点O是等边△ABC内一点，∠AOB＝110°，∠BOC=α, 以OC为边作等边三角形OCD，连接AD．

（1）①求证：△BOC≌△ADC；
②当α＝150°时，试判断△AOD的形状，并说明理由；
（2）探究：当∠1为多少度时，△AOD是等腰三角形？
参考答案
一、1~5：CDCAD 6~10：BCCBB
二、11.-1 12.72 13.1.5 14. 15.30°
三、16. 【小问1详解】
解：
=
=
=；
【小问2详解】

=
=
=
17. 【小问1详解】
解：
=
=
=；
小问2详解】

=
=
18.


，
当，时，原式．
19.【小问1详解】
解：∵点A表示的数是1，点B表示的数是．
∴，
∵点B，C关于A成中心对称，
∴，
∴点C表示的数为；
故答案为：；
【小问2详解】
解：∵点C表示的数为a，
∴，
∵，
∴，
∴，
∵a的小数部分为b，
∴，
∴．
20. 【小问1详解】
解：∵，
∴该同学第二步到第三步运用了因式分解的完全平方公式．
故选：C
【小问2详解】
解：设，
原式


．
21.【小问1详解】
解：∵，
∴，
∵，
∴，
∴，
在和中，，
∴，
∴；
【小问2详解】
为等腰直角三角形，理由：
∵点F是中点，
∴，
在和中，
∵，
∴，
∴，，
∵，
∴，，
∴，
∴为等腰直角三角形．
故答案为：等腰直角．
22. （1）观察图形，可得：2a2+5ab+2b2
=（a+2b）（2a+b）．
故答案为：（a+2b）（2a+b）．
（2）∵图中阴影部分的面积为20平方厘米，大长方形纸板的周长为24厘米．
∴2a2+2b2=20，2（a+2b+2a+b）=24．
∴a2+b2=10，a+b=4．
∵（a+b）2=a2+b2+2ab．
∴16=10+2ab．
∴ab=3．
2a2+5ab+2b2=2×10+5×3=35（平方厘米）．
空白部分面积为：35-20=15（平方厘米）．
23. 【小问1详解】
①证明：∵△ABC和△ODC是等边三角形，
∴∠ABC＝∠CAB＝∠ODC＝∠DOC＝60°，
BC＝AC，CO＝CD，
∴∠ACB﹣∠ACO＝∠DCO﹣∠ACO，
∴∠ACD＝∠BCO，
在△BOC和△ADC中，
，
∴△BOC≌△ADC（SAS）；
②解：△ADO是直角三角形．
理由如下：∵△BOC≌△ADC，
∴∠BOC＝∠ADC，
∵∠BOC＝α＝150°，∠ODC＝60°，
∴∠ADO＝150°﹣60°＝90°，
∴△ADO是直角三角形；
【小问2详解】
解：由题意可得：∠COB＝∠CDA＝α，∠AOD＝190°﹣α，∠OAD＝50°，
当OA＝AD时，
∵AO＝AD，CO＝CD，
∴AC垂直平分OD，
∵AO＝AD，
∴∠OAC＝∠OAD＝25°，
∴∠7＝35°；
当AO＝OD时，
∵OA＝OD，
∴∠OAD＝∠ADO，
∴α﹣60°＝50°，
∴α＝110°，
∴∠AOD＝80°，
∴∠AOC＝140°，
∵AO＝OD＝OC，
∴∠OAC＝20°＝∠ACO，
∴∠1＝40°，
当OD＝AD时，
∵OD＝AD，
∴∠OAD＝∠AOD，
∴190°﹣α＝50°，
∴α＝140°．
∴∠ADC＝140°，
∵AD＝CD，
∴∠DAC＝DCA＝20°，
∴∠OAC＝30°，
∴∠1＝30°，
综上所述，∠1为35°或40°或30°．