2023年山东省青岛市西海岸新区中考数学一模试卷（word版含答案解析）

这是一份2023年山东省青岛市西海岸新区中考数学一模试卷（word版含答案解析），共30页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2023年山东省青岛市西海岸新区中考数学一模试卷
一、选择题（本大题共10小题，每小题3分，共30分）
1．（3分）若一个数的绝对值是，则这个数是（　　）
A． B． C．或 D．或
2．（3分）剪纸是一项传统的民间文化艺术，也是我国的非物质文化遗产之一，下列剪纸图案中不是中心对称图形的是（　　）
A． B．
C． D．​​​​
3．（3分）在一个不透明的盒子中装有a个黑白颜色的球，小明又放入了4个红球，这些球大小相同．若每次将球充分搅匀后，任意摸出1个球记下颜色再放回盒子．通过大量重复试验后，发现摸到红球的频率稳定在20%左右，则a的值大约为（　　）
A．10 B．16 C．25 D．30
4．（3分）某中学篮球队12名队员的年龄情况如下表，关于这12名队员的年龄，下列说法中正确的是（　　）
年龄/岁
12
13
14
15
16
人数
1
3
4
2
2
A．众数为14 B．极差为3 C．中位数为13 D．平均数为14
5．（3分）下列运算正确的是（　　）
A．a2•a3＝a6 B．（﹣2x）2＝4x2 C． D．ab2﹣ab＝b
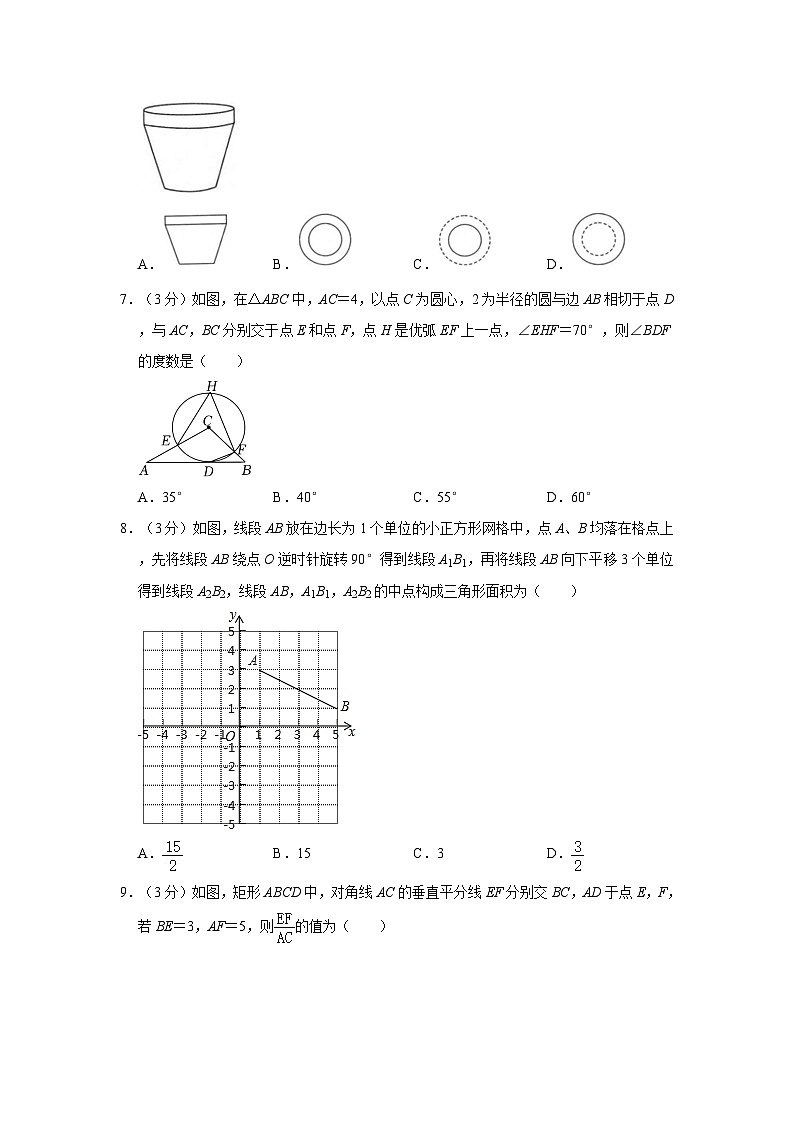
6．（3分）如图所示的是空心花盆的示意图，则它的俯视图是（　　）

A． B． C． D．
7．（3分）如图，在△ABC中，AC＝4，以点C为圆心，2为半径的圆与边AB相切于点D，与AC，BC分别交于点E和点F，点H是优弧EF上一点，∠EHF＝70°，则∠BDF的度数是（　　）

A．35° B．40° C．55° D．60°
8．（3分）如图，线段AB放在边长为1个单位的小正方形网格中，点A、B均落在格点上，先将线段AB绕点O逆时针旋转90°得到线段A1B1，再将线段AB向下平移3个单位得到线段A2B2，线段AB，A1B1，A2B2的中点构成三角形面积为（　　）

A． B．15 C．3 D．
9．（3分）如图，矩形ABCD中，对角线AC的垂直平分线EF分别交BC，AD于点E，F，若BE＝3，AF＝5，则的值为（　　）

A． B． C． D．
10．（3分）一次函数y＝kx+b（k≠0）与二次函数y＝ax2+2ax+c（a≠0）在同一平面直角坐标系中的图象如图所示，则下列说法错误的是（　　）

A．ax2+2ax﹣b＞kx﹣c时，n＜x＜m
B．当x≥0时，ax2+2ax+c≤c
C．若（﹣，y1）在二次函数y＝ax2+2ax+c图象上，则y1＜c
D．﹣ac+bk＞0
二、填空题（本大题共6小题，每小题3分，共18分）
11．（3分）因式分解2m2﹣4m+2＝　 　．
12．（3分）在国家大数据战略的引领下，我国在人工智能领域取得显著成就．某大数据中心存储约30800000000本电子书籍，将30800000000用科学记数法表示应为 　 　．
13．（3分）已知一元二次方程ax2﹣x+1＝0（a≠0），有两个实数根，则a的取值范围是　 　．
14．（3分）如图，是甲、乙两人10次射击成绩（环数）的条形统计图，如果甲又连续射击了5次，且环数均为9环，那么　 　（填“＜”、“＝”或“＞”）．
​
15．（3分）如图，半圆O的直径AB＝3，．E是上一个动点，弦DE∥AB，OF⊥AB，交DE于点F．OH＝EF．则图中阴影部分周长的最大值为 　 　．
​

16．（3分）如图，正方形ABCD的边长为a，点E在边AB上运动且不与点A、B重合，∠DAM＝45°，点F在射线AM上，且，CF与AD相交于点G，连结EC、EF，EG．则下列结论正确的是 　 　．（填写序号）
①EG＝BE+DG；
②△AEG的周长为2a；
③△EAF的面积的最大值是；
④当BE：AE＝1：2时，G是线段AD的中点．

三.作图题（本题满分4分）
17．（4分）已知：如图，在△ABC中，∠A为钝角．
求作：⊙P，使圆心P在△ABC的边AC上，且⊙P与AB、BC所在的直线都相切．
（要求：尺规作图，不写作法，保留作图痕迹）

四、解答题（本大题共9小题，共78分）
18．（8分）（1）计算：；
（2）解不等式组：．
19．（6分）4张相同的卡片分别写有数字1，2，3，4，将卡片的背面朝上，洗匀后从中任意抽取1张，将卡片上的数字作为被减数；一只不透明的袋子中装有标号为1，2，3的3个小球，这些球除标号外都相同，搅匀后从中任意摸出一个球，将摸到的球的标号作为减数．
（1）求这两个数的差为0的概率；（用列表法或树状图说明）
（2）如果游戏规则规定：当抽到的这两个数的差为非负数时，则甲获胜；当抽到的这两个数的差为非正数时，则乙获胜；你认为这样的规则公平吗？如果不公平，请设计一个你认为公平的规则，并说明理由．
20．（6分）某校为了解初三年级学生的身高情况，从中随机抽取了40名学生的身高数据，并对数据进行整理、描述和分析，给出了部分信息．
a．40名学生身高的频数分布表和频数分布直方图；
40名学生身高的频数分布表（表1）：
身高x（cm）
频数
频率
150≤x＜155
4
0.100
155≤x＜160
a
0.300
160≤x＜165
7
0.175
165≤x＜170
b
m
170≤x＜175
8
0.200
175≤x＜180
2
0.050
合计
40
1.000
b.40名学生身高在160≤x＜165这一组的数据如表（表2）所示：
身高（cm）
160
161
162
163
164
频数
1
0
1
2
3
根据以上信息，回答下列问题：
（1）表1中a的值为 　 　；
（2）补全该校40名学生身高频数分布直方图；
（3）样本数据的中位数是 　 　；
（4）若该校初三年级共600名学生，请估计身高不低于165cm的学生有多少人？

21．（6分）如图，斜坡BC的坡度为1：6，坡顶B到水平地面（AD）的距离AB为3米，在B处、C处分别测得ED顶部点E的仰角为26.6°和56.3°，点 A、C、D在一直线上，求DE（DE⊥AD）的高度（精确到1米）．
（参考数据：sin26.6°≈0.45，cos26.6°≈0.89，tan26.6°≈0.5，sin56.3°≈0.83，cos56.3°≈0.55，tan56.3°≈1.5）

22．（6分）如图，直线y＝x+1与y轴交于A点，与反比例函数（x＞0）的图象交于点M，过M作MH⊥x轴于点H，且tan∠AHO＝．
（1）求k的值；
（2）设点N（1，a）是反比例函数（x＞0）图象上的点，在y轴上是否存在点P，使得PM+PN最小？若存在，求出点P的坐标；若不存在，请说明理由．

23．（8分）如图，在平行四边形ABCD中，O是DC的中点，连接AO延长交BC的延长线于E，过点B作AO的平行线交DC的延长于点F．
（1）证明：△EOC≌△AOD；
（2）若AE是∠BAD的角平分线，请判断四边形BFEO是什么特殊四边形，请说明理由．

24．（8分）【探究】（1）观察下列算式，并完成填空：
1＝12
1+3＝4＝22
1+3+5＝9＝32
1+3+5+7＝16＝42；
1+3+5．…+（2n﹣1）＝　 　.（n是正整数）
（2）如图是某市一广场用正六边形、正方形和正三角形地板砖铺设的图案，图案中央是一块正六边形地板砖，周围是正方形和正三角形的地板砖．从里向外第一层包括6块正方形和6块正三角形地板砖；第二层包括6块正方形和18块正三角形地板砖；以此递推．
①第3层中分别含有 　 　块正方形和 　 　块正三角形地板砖；
②第n层中分别含有 　 　块正方形和 　 　块正三角形地板砖（用含n的代数式表示）．
【应用】
该市打算在一个新建广场中央，采用如图样式的图案铺设地面，现有1块正六边形、150块正方形地板砖，问：铺设这样的图案，还需要多少块正三角形地板砖？请说明理由．

25．（10分）第二十四届冬奥会在北京成功举办，我国选手在跳台滑雪项目中夺得金牌．在该项目中，运动员首先沿着跳台助滑道飞速下滑，然后在起跳点腾空，身体在空中飞行至着陆坡着陆，再滑行到停止区终止．本项目主要考核运动员的飞行距离和动作姿态，某数学兴趣小组对该项目中的数学问题进行了深入研究：
如图为该兴趣小组绘制的赛道截面图，以停止区CD所在水平线为x轴，过起跳点A与x轴垂直的直线为y轴，O为坐标原点，建立平面直角坐标系．着陆坡AC的坡角为30°，OA＝65m，某运动员在A处起跳腾空后，飞行至着陆坡的B处着陆，AB＝100m．在空中飞行过程中，运动员到x轴的距离y（m）与水平方向移动的距离x（m）具备二次函数关系，其解析式为y＝﹣x2+bx+c．
（1）求b，c的值；
（2）进一步研究发现，运动员在飞行过程中，其水平方向移动的距离x（m）与飞行时间t（s）具备一次函数关系，当运动员在起跳点腾空时，t＝0，x＝0；空中飞行5s后着陆．
①求x关于t的函数解析式；
②当t为何值时，运动员离着陆坡的竖直距离h最大，最大值是多少？


26．（10分）如图，已知Rt△ACB和Rt△DCE中，∠ACB＝∠DCE＝90°，AC＝CD＝4，BC＝CE＝3，B、C、D共线．动点P从D点出发沿DB向B点运动；动点Q从B点出发沿BA向A点运动；速度均为1cm/s，当Q点到达A点时，P，Q两点停止运动，过P点作DE的垂线，垂足为M点，连接PQ，PM，QM（0＜t＜5），解答下列问题：
（1）当PQ⊥AB时，求t的值；
（2）设△QPM的面积为S（cm2），求S与t的函数关系式；
（3）是否存在某一时刻t，使得点Q在PM的垂直平分线上？若存在，求t的值；若不存在，请说明理由．
























参考答案与试题解析
一、选择题（本大题共10小题，每小题3分，共30分）
1．【答案】C
【分析】根据绝对值等于一个正数的数有两个解决此问题．
【解答】解：一个数的绝对值是，则这个数是±，
故选：C．
2．【答案】B
【分析】根据中心对称图形的概念，把一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形，求解判断即可．
【解答】解：A、该图形是中心对称图形，不符合题意；
B、该图形不是中心对称图形，符合题意；
C、该图形是中心对称图形，不符合题意；
D、该图形是中心对称图形，不符合题意．
故选：B．
3．【答案】B
【分析】在同样条件下，大量反复试验时，随机事件发生的频率逐渐稳定在概率附近，可以从比例关系入手，列出方程求解．
【解答】解：由题意可得，×100%＝20%，
解得，a＝16，
经检验：a＝16是原分式方程的解，
所以a＝16，
故选：B．
4．【答案】A
【分析】根据众数、中位数、平均数与极差的定义逐一计算即可判断．
【解答】解：由图表可得：14岁的有4人，故众数是14，故选项A符合题意；
极差是：16﹣12＝4，故选项B不合题意；
中位数是：＝14，故选项C不合题意；
平均数是：（12+13×3+14×4+15×2+16×2）÷12＝14.75，故选项D不合题意．
故选：A．
5．【答案】B
【分析】根据同底数幂的乘法，幂的乘方与积的乘方，负整数指数幂，合并同类项法则，进行计算逐一判断即可解答．
【解答】解：A、a2⋅a3＝a5，故A不符合题意；
B、（﹣2x）2＝4x2，故B符合题意；
C、，故C不符合题意；
D、ab2与﹣ab不能合并，故D不符合题意；
故选：B．
6．【答案】B
【分析】找出从几何体的上面看所得到的图形即可．
【解答】解：从几何体的上面看可得两个同心圆，
故选：B．
7．【答案】B
【分析】连接CD，由切线的性质得出CD⊥AB，∠CDB＝90°，利用解直角三角形求出∠ACD＝60°，由圆周角定理求出∠ACB＝140°，进而求出∠DCB＝80°，再利用等腰三角形的性质求出∠CDF的度数，继而求出∠BDF的度数．
【解答】解：如图，连接CD，

∵AB是⊙C的切线，
∴CD⊥AB，
∴∠CDB＝90°，
∵AC＝4，CD＝2，
∴cos∠ACD＝＝＝，
∴∠ACD＝60°，
∵∠EHF＝70°，
∴∠ACB＝2∠EHF＝140°，
∴∠DCB＝∠ACB﹣∠ACD＝140°﹣60°＝80°，
∵CD＝CF，
∴∠CDF＝∠CFD＝＝50°，
∴∠BDF＝∠CDB﹣∠CDF＝90°﹣50°＝40°，
故选：B．
8．【答案】A
【分析】首先作出线段A1B1和A2B2，确定线段AB，A1B1，A2B2的中点，作出三角形，利用三角形的面积公式求解．
【解答】解：三角形的面积是：×3×5＝．
故选：A．

9．【答案】A
【分析】连接AE，由线段垂直平分线的性质得出OA＝OC，AE＝CE，证明△AOF≌△COE得出AF＝CE＝5，得出AE＝CE＝5，BC＝BE+CE＝8，由勾股定理求出AB＝4，再由勾股定理求出AC，再求得EF的长即可．
【解答】解：设AC与EF交于点O，连接AE，如图：
∵EF是AC的垂直平分线，
∴OA＝OC，AE＝CE，
∵四边形ABCD是矩形，
∴∠B＝90°，AD∥BC，
∴∠OAF＝∠OCE，
在△AOF和△COE中，
，
∴△AOF≌△COE（ASA），
∴AF＝CE＝5，
∴AE＝CE＝5，BC＝BE+CE＝3+5＝8，
∴AB＝＝＝4，
∴AC＝＝＝4，
∴AO＝2，
∴EO＝＝，
∴EF＝2，
∴＝＝．
故选：A．

10．【答案】C
【分析】A选项将ax2+2ax﹣b＞kx﹣c，移项可得，ax2+2ax+c＞kx+b，根据图象求解判断为对；
B选项当x≥0时，抛物线最高点（即ax2+2ax﹣b的最大值）为抛物线与y的交点，此点为（0，c），即可求解判断为对；
C选项抛物线的对称轴是直线x＝﹣＝﹣1，所以在抛物线上与点（0，c）关于对称轴x＝﹣1对称的点是（﹣2，c），但是﹣2＜﹣＜﹣1，所以，y1＞c，可判断为错；
D选项因为抛物线开口向下，且与y轴交点在正半轴，所以，a＜0，c＞0，因为直线经过二、四象限，且与y轴交于负半轴，所以k＜0，b＜0，即可判断为对．
【解答】解：A选项，对于ax2+2ax﹣b＞kx﹣c，移项可得，ax2+2ax+c＞kx+b，对应于图中即是抛物线在直线上方的部分，由图可知，两个曲线交点的x坐标为x＝n和x＝m，所以，n＜x＜m，所以A正确；
B选项，当x≥0时，抛物线最高点（即ax2+2ax+c的最大值）为抛物线与y的交点，此点为（0，c），所以，当x≥0时，ax2+2ax+c≤c，所以B正确；
C选项，在抛物线中，有对称轴公式可知，抛物线的对称轴是直线x＝﹣＝﹣1，所以在抛物线上与点（0，c）关于对称轴x＝﹣1对称的点是（﹣2，c），但是﹣2＜﹣＜﹣1，所以，y1＞c，所以C错误；
D选项，因为抛物线开口向下，且与y轴交点在正半轴，所以，a＜0，c＞0，因为直线经过二、四象限，且与y轴交于负半轴，所以k＜0，b＜0，所以，﹣ac+bk＞0，D正确．
故选：C．
二、填空题（本大题共6小题，每小题3分，共18分）
11．【答案】2（m﹣1）2．
【分析】直接提取公因式2，进而利用完全平方公式分解因式即可．
【解答】解：原式＝2（m2﹣2m+1）
＝2（m﹣1）2．
故答案为：2（m﹣1）2．
12．【答案】3.08×1010．
【分析】把一个大于10的数记成a×10n的形式，其中a是整数数位只有一位的数，n是正整数，这种记数法叫做科学记数法，由此即可得到答案．
【解答】解：30800000000＝3.08×1010．
故答案为：3.08×1010．
13．【答案】a≤且a≠0．
【分析】由关于x的一元二次方程ax2﹣x+1＝0有两个实数根，即可得判别式△≥0且a≠0，继而可求得a的取值范围．
【解答】解：∵关于x的一元二次方程ax2﹣x+1＝0有两个实数根，
∴Δ＝b2﹣4ac＝（﹣1）2﹣4×a×1＝1﹣4a≥0，
解得：a≤，
∴a的取值范围是a≤且a≠0．
故答案为：a≤且a≠0．
14．【答案】＜．
【分析】根据方差的计算方法进行计算即可．
【解答】解：甲15次射击成绩的平均数是9环，
所以＝[（8﹣9）2×4+（10﹣9）2×4]＝≈0.53；
乙10次射击成绩的平均数9环，
所以＝[（8﹣9）2×3+（10﹣9）2×3]＝＝0.6，
因此＜，
故答案为：＜．
15．【答案】．
【分析】连接OE，可证四边形HOEF是平行四边形，则DF+AH+HF＝3，所以当E与C点重合时，AD弧的长最大，可求∠BOC＝45°，即可求AD弧的长＝，进而求阴影部分周长的最大值．
【解答】解：连接OE，
∵DE∥AB，OH＝EF，
∴四边形HOEF是平行四边形，
∴HF＝OE，
∵HO＝EF，
∴DF+AH＝AO，
∴DF+AH+HF＝AO+OE＝AB，
∵AB＝3，
∴DF+AH+HF＝3，
∵点E是上一个动点，
∴当E与C点重合时，AD弧的长最大，
此时阴影部分周长最大，
∵＝3，
∴∠BOC＝45°，
∴AD弧的长＝＝π，
∴阴影部分周长的最大值为π+3，
故答案为：π+3．



16．【答案】①②③④．
【分析】①②正确，如图2中，延长AD到H，使得DH＝BE，则△CBE≌△CDH（SAS），再证明△GCE≌△GCH（SAS）即可解决问题；
③正确．设BE＝x，则AE＝a﹣x，AF＝x，构建二次函数，利用二次函数的性质解决最值问题；
④正确．当BE：AE＝1：2时，设DG＝x，则EG＝x+a，利用勾股定理构建方程可得x＝a即可解决问题．
【解答】解：如图中，延长AD到H，使得DH＝BE，连接CH，则△CBE≌△CDH（SAS），

∴∠ECB＝∠DCH，
∴∠ECH＝∠BCD＝90°，
∴∠ECG＝∠GCH＝45°，
∵CG＝CG，CE＝CH，
∴△GCE≌△GCH（SAS），
∴EG＝GH，
∵GH＝DG+DH，DH＝BE，
∴EG＝BE+DG，故①正确，
∴△AEG的周长＝AE+EG+AG＝AE+AH＝AD+DH+AE＝AE+EB+AD＝AB+AD＝2a，故②正确，
设BE＝x，则AE＝a﹣x，AF＝x，
∴S△EAF＝（a﹣x）×x＝﹣x2+ax＝﹣（x2﹣ax+a2﹣a2）＝﹣（x﹣a）2+a2，
∵﹣＜0，
∴x＝a时，△EAF的面积的最大值为a2．故③正确，
当BE：AE＝1：2时，BE＝AB＝a，
设DG＝x，
∵EG＝BE+DG，
∴EG＝x+a，
在Rt△AEG中，则有（x+a）2＝（a﹣x）2+（a）2，
解得x＝，
∴AG＝GD，故④正确，
故答案为：①②③④．
三.作图题（本题满分4分）
17．【答案】作图见解析部分．
【分析】作∠ABC的角平分线BP，过点P作PD⊥BC于D，以P为圆心，PD为半径作⊙P即为．
【解答】解：如图，⊙P即为所求．

四、解答题（本大题共9小题，共78分）
18．【答案】（1）；
（2）﹣2＜x＜．
【分析】（1）先计算括号内的，然后计算除法即可；
（2）先把分子分母因式分解，然后约分化简，再代入求解即可．
【解答】解：（1）原式＝÷[﹣+]
＝÷
＝•
＝；
（2）由3（1﹣x）＜﹣2x+5，得：x＞﹣2，
由1﹣＞，得：x＜，
则不等式组的解集为﹣2＜x＜．
19．【答案】（1）；
（2）不公平．两个数的差为正数时，甲获胜，否则，乙获胜．
【分析】（1）利用树状图法列举出所有可能，进而求出概率；
（2）利用概率公式进而得出甲、乙获胜的概率即可得出答案．
【解答】解：（1）列表如下：

1
2
3
4
1
0
1
2
3
2
﹣1
0
1
2
3
﹣2
﹣1
0
1
∵共有12种等可能的结果，其中两个数的差为0的情况占3种，
∴P（两个数的差为0）＝．

（2）不公平．
∵两个数的差为非负数的情况有9种，
∴P（甲获胜）＝，P（乙获胜）＝．
∵P（甲获胜）＞P（乙获胜），
∴这样的规则不公平，
可将规则改为：两个数的差为正数时，甲获胜，否则，乙获胜．
此时P（甲获胜）＝P（乙获胜）＝．
20．【答案】（1）12；
（2）补全图形见解答过程；
（3）163.5cm；
（4）255人．
【分析】（1）根据频数＝样本容量×频率求解即可；
（2）先根据频数之和等于样本容量求出b的值，从而补全图形；
（3）找到这组数据的第20、21个数据，求平均数即可得出答案；
（4）总人数乘以样本中身高不低于165cm的学生人数所占比例．
【解答】解：（1）a＝40×0.3＝12，
故答案为：12；
（2）b＝40﹣（4+12+7+8+2）＝7，
补全图形如下：

（3）由题意知，第20、21个数据分别为163、164，
所以样本数据的中位数是＝163.5（cm），
故答案为：163.5cm；
（4）估计身高不低于165cm的学生有600×＝255（人），
答：估计身高不低于165cm的学生有255人．
21．【答案】见试题解答内容
【分析】过点B作BF⊥CD，垂足为F，设EF＝x米，根据锐角三角函数可得BF＝2x米，然后根据斜坡BC的坡度为1：6，坡顶B到水平地面（AD）的距离AB为3米，可得AC＝18米，AB＝DF＝3米，所以ED＝EF+FD＝（x+3）米，进而可以解决问题．
【解答】解：过点B作BF⊥CD，垂足为F，

则AB＝DF，BF＝AD，
设EF＝x米，
在Rt△EBF中，∠EBF＝26.6°，
∴EF＝BF•tan26.6°，
∴x≈BF×0.5，
∴BF＝2x米，
∵斜坡BC的坡度为1：6，坡顶B到水平地面（AD）的距离AB为3米，
∴AC＝18米，AB＝DF＝3米，
∴ED＝EF+FD＝（x+3）米，
在Rt△DEC中，∠ECD＝56.3°，
∴ED＝CD•tan56.3°，
∴x+3≈CD×1.5，
∴CD＝（x+3）米，
∵BF＝AD＝AC+CD，
∴2x＝18+（x+3），
解得，x＝15，
∴EF＝15米，
∴ED＝EF+FD＝15+3＝18（米），
∴DE的高度是18米．
22．【答案】见试题解答内容
【分析】（1）对于直线y＝x+1，令x＝0求出y的值，确定出A坐标，得到OA的长，根据tan∠AHO的值，利用锐角三角函数定义求出OH的长，根据MH垂直于x轴，得到M横坐标与A横坐标相同，再由M在直线y＝x+1上，确定出M坐标，代入反比例解析式求出k的值即可；
（2）将N坐标代入反比例解析式求出a的值，确定出N坐标，过N作N关于y轴的对称点N1，连接MN1，交y轴于P（如图），此时PM+PN最小，由N与N1关于y轴的对称，根据N坐标求出N1坐标，设直线MN1的解析式为y＝kx+b，把M，N1的坐标代入求出k与b的值，确定出直线MN1的解析式，令x＝0求出y的值，即可确定出P坐标．
【解答】解：（1）由y＝x+1可得A（0，1），即OA＝1，
∵tan∠AHO＝＝，
∴OH＝2，
∵MH⊥x轴，
∴点M的横坐标为2，
∵点M在直线y＝x+1上，
∴点M的纵坐标为3，即M（2，3），
∵点M在y＝上，
∴k＝2×3＝6；
（2）∵点N（1，a）在反比例函数y＝的图象上，
∴a＝6，即点N的坐标为（1，6），
过N作N关于y轴的对称点N1，连接MN1，交y轴于P（如图），
此时PM+PN最小，
∵N与N1关于y轴的对称，N点坐标为（1，6），
∴N1的坐标为（﹣1，6），
设直线MN1的解析式为y＝kx+b，
把M，N1的坐标得，
解得：，
∴直线MN1的解析式为y＝﹣x+5，
令x＝0，得y＝5，
∴P点坐标为（0，5）．

23．【答案】（1）答案见解答过程；
（2）四边形BFEO是矩形，理由见解答过程．
【分析】（1）先证四边形ABFO为平行四边形，然后根据平行四边形的性质得CF＝OC，再证△CBF和△CEO全等得BF＝EO＝AO，据此可依据“SAS”判定△EOC和△AOD全等；
（2）先根据角平分线的性质及AD∥BD证∠BAE＝∠BEA，进而得AB＝BE，再证四边形BFEO为平行四边形，然后再根据矩形的判定可得出结论．
【解答】（1）证明：∵四边形ABCD为平行四边形，
∴AB∥CD，AB＝CD，
∴AB∥OF，
又∵BF∥AO，
∴四边形ABFO为平行四边形，
∴BF＝AO，BF∥AO，AB＝OF，
∵点O为CD的中点，
∴，
∴，
∴，
∵AB＝OF
∴，
∴，
∴CF＝OC，
∵BF∥AO，
∴∠CBF＝∠CEO，∠CFB＝∠COE，
在△CBF和△CEO中，
，
∴△CBF≌△CEO（AAS），
∴BF＝EO，
∴EO＝AO，
在△EOC和△AOD中，

∴△EOC≌△AOD（SAS）；
（2）解：四边形BFEO是矩形，理由如下：
∵AE是∠BAD的角平分线，
∴∠DAE＝∠BAE，
∵四边形ABCD为平行四边形，
∴AD∥BC，
∴∠DAE＝∠BEA，
∴∠BAE＝∠BEA，
∴AB＝BE，
由（1）可知：四边形ABFO为平行四边形，
∴AB＝OF，
∴BE＝OF，
由（1）可知：△CBF≌△CEO（AAS），
∴BF＝OE，
又∵BF∥AO，
∴四边形BFEO为平行四边形，
∵BE＝OF，
∴平行四边形BFEO为矩形．
24．【答案】（1）n2；
（2）①6，30；
②6，6（2n﹣1）；
【应用】铺设这样的图案，还需要3750块正三角形地板砖．理由见解答．
【分析】【探究】（1）观察算式找出规律即可；
（2）①第一层6块正方形和6块正三角形地板砖，第二层6块正方形和6+12＝18块正三角形地板砖，第三层6块正方形和18+12＝30块正三角形地板砖；
②每一层中正方形地板砖块数不变；正三角形地板砖的块数分别为：第一层6＝6×1＝6×（2×1﹣1）块，第二层18＝6×3＝6×（2×2﹣1）块，第三层30＝6×5＝6×（2×3﹣1）块，由此得出第n层6＝6×1＝6（2n﹣1）块；
【应用】150块正方形地板砖可以铺设这样的图案150÷6＝25（层），铺设n层需要正三角形地板砖的数量为：6[1+3+5+…+（2n﹣1）]＝6n2，将n＝25代入计算即可．
【解答】解：（1）观察算式规律可得，1+3+5+…+（2n﹣1）＝n2，
故答案为：n2；
（2）①∵第一层包括6块正方形和6块正三角形地板砖，
第二层包括6块正方形和6+12＝18块正三角形地板砖，
∴第三层包括6块正方形和18+12＝30块正三角形地板砖．
故答案为：6，30；
②∵每一层中正方形地板砖块数不变；
正三角形地板砖的块数分别为：
第一层6＝6×1＝6×（2×1﹣1）块，
第二层18＝6×3＝6×（2×2﹣1）块，
第三层30＝6×5＝6×（2×3﹣1）块，
∴第n层6（2n﹣1）块正三角形地板砖．
故答案为：6，6（2n﹣1）；
【应用】铺设这样的图案，还需要3750块正三角形地板砖．理由如下：
∵150÷6＝25（层），
∴150块正方形地板砖可以铺设这样的图案25层；
∵铺设n层需要正三角形地板砖的数量为：6[1+3+5+⋯+（2n﹣1）]＝6n2，
∴当n＝25时，6×252＝3750．
故铺设这样的图案，还需要3750块正三角形地板砖．
25．【答案】（1）b的值是，c的值是65；
（2）①x＝10t；
②当t为2.5时，运动员离着陆坡的竖直距离h最大，最大值是m．
【分析】（1）根据题意，可以求得点A和点B的坐标，然后代入二次函数解析式，即可得到b、c的值；
（2）①根据题意，可以得到x关于t的函数图象经过的两个点，然后根据待定系数法，即可得到x关于t的函数的解析式；
②先求出直线AB的解析式，再根据题意，可以表示出h，然后根据二次函数的性质，可以求得当h为何值时，运动员离着陆坡的竖直距离h最大，并求出这个最大值．
【解答】解：（1）作BE⊥y轴于点E，
∵OA＝65m，着陆坡AC的坡角为30°，AB＝100m，
∴点A的坐标为（0，65），AE＝50m，BE＝50m，
∴OE＝OA﹣AE＝65﹣50＝15（m），
∴点B的坐标为（50，15），
∵点A（0，65），点B（50，15）在二次函数y＝﹣x2+bx+c的图象上，
∴，
解得，
即b的值是，c的值是65；
（2）①设x关于t的函数解析式是x＝kt+m，
因为点（0，0），（5，50）在该函数图象上，
∴，
解得，
即x关于t的函数解析式是x＝10t；
②设直线AB的解析式为y＝px+q，
∵点A（0，65），点B（50，15）在该直线上，
∴，
解得，
即直线AB的解析式为y＝﹣x+65，
则h＝（﹣x2+x+65）﹣（﹣x+65）＝﹣x2+x，
∴当x＝﹣＝25时，h取得最值，此时h＝，
∵25＜50，
∴x＝25时，h取得最值，符合题意，
将x＝25代入x＝10t，得：25＝10t，
解得t＝2.5，
即当t为2.5时，运动员离着陆坡的竖直距离h最大，最大值是m．

26．【答案】（1）t＝s；
（2）S＝﹣（0＜t＜5）；
（3）t＝s．
【分析】（1）根据cosB＝得，从而得出t＝；
（2）可推出PM∥AB，从而PM＝PD•sinD＝t•＝，进而得出S的函数关系式；
（3）作PG⊥AB于G，作QH⊥PM于H，可推出当PM＝2QG＝2PH时，PQ＝QM，即Q在PM的垂直平分线上，可表示出BG＝（7﹣t），BQ＝t，QG＝t﹣（7﹣t）＝，从而列出方程t＝2（），进一步得出结果．
【解答】解：（1）∵PQ⊥AB，
∴∠PQB＝∠ACB＝90°，
∵BC＝3，BC＝4，
∴AB＝5，
∴cosB＝，
∴，
∴t＝s；
（2）如图1，

作PG⊥AB于G，
PG＝PB•sinB＝（7﹣t），
∵∠ACB＝∠DCE＝90°，AC＝CD，BC＝CE，
∴△ACB≌△DCE（SAS），
∴∠D＝∠A，
∵∠A+∠B＝90°，
∴∠D+∠B＝90°，
∵PM⊥DE，
∴∠PMD＝90°，
∴∠D+∠DPM＝90°，
∴∠B＝∠DPM，
∴PM∥AB，
∵PM＝PD•sinD＝t•＝，
∴S＝PM•PG＝×（7﹣t）＝﹣（0＜t＜5）；
（3）如图2，

存在t＝s，使得点Q在PM的垂直平分线上，理由如下：
作PG⊥AB于G，作QH⊥PM于H，
∴∠PGQ＝∠QHP＝90°，
∵PM∥AB，
∴∠GPH＝180°﹣∠PGQ＝90°，
∴四边形PGQH是矩形，
∴QG＝PH，
当PM＝2QG＝2PH时，PQ＝QM，即Q在PM的垂直平分线上，
∵BG＝（7﹣t），BQ＝t，
∴QG＝t﹣（7﹣t）＝，
∴t＝2（），
∴t＝＜5，
∴当t＝s时，点Q在PM的垂直平分线上．