


2017年青海省中考数学试卷及答案
展开青海省2017年初中毕业升学数学试卷
一、填空题(本大题共12小题15空,每空2分,共30)
1.-7×2的绝对值是_____;![]() 的平方根是_____.
的平方根是_____.
2.分解因式ax2-2ax+a=_____;计算:![]() = _____.
= _____.
3.中国倡导的“一带一路”建设将促进我国与世界各国的互利合作,根据规划“一带一路”覆盖地区总人口约为4400000000人,这个数用科学记数法表示为_____.
4.如图1,在平面上将边长相等的正三角形、正方形、正五边形、正六边形的一边重合并叠在一起,则∠3+∠1-∠2= _____.
5.如图2,在△ABC中,∠ABC和∠ACB的角平分线相交于点O,若∠A=50°,则∠BOC= _____.
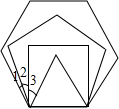
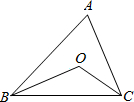
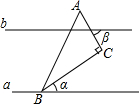
图1 图2 图3
6.如图3,直线a∥b,Rt△ABC的顶点B在直线a上,∠C=90°,∠β=55°,则∠a的度数为_____.
7.若单项式2x2ym与-![]() xny4可以合并成一项,则nm=_____.
xny4可以合并成一项,则nm=_____.
8.有两个不透明的盒子,第一个盒子中有3张卡片,上面的数字分别为1,2,2;第二个盒子中有5张卡片,上面的数字分别为1,2,2,3,3.这些卡片除了数字不同外,其它都相同。从每个盒子中各抽出一张,都抽到卡片数字是2的概率为_____.
9.已知扇形的圆心角为240°,所对的弧长为![]() ,则此扇形的面积是_____.
,则此扇形的面积是_____.
10.如图4,在一个4×4的网格中,每个小正方形的边长均为1,每个小正方形的顶点叫做格点,点A在格点上,动点P从A点出发,先向右移动2个单位长度到达P1,P1绕点A针旋转90°到达P2,P2再向下移动2个单位长度回到A点,P点所经过的路径围成的图形____图形。(填“轴对称”或”中心对称”)
11.如图5所示,小芳在中心广场放风筝,已知风筝拉线长100米(假设拉线是直的),且拉线与水平地面的夹角为60°,若小芳的身高忽略不计,则风筝离水平地面的高度是_____.米(结果保留根号)。

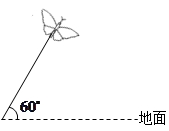
图4 图5
12.观察下列各式的规律:
(x-1)(x+1)=x2-1
(x-1)(x2+x+1)=x3-1
(x-1)(x3+x2+x+1)=x4-1
……
可得到(x-1)(x7+x6+x5+x4+x3+x2+x+1)= _____;
一般地(x-1)(xn+xn-1+…+x2+x+1)= _____.
二、选择题(本大题共8小题,每小题3分,共24分,每小题给出的四个选项中,只有一个选项符合要求,请把你认为正确的选项序号填入下面相应题号的表格内).
13.估计2+![]() 的值( )
的值( )
A.在2和3之间 B.在3和4之间 C.在4和5之间 D.在5和6之间
14.在某次测试后,班里有两位同学议论他们小组的数学成绩,小明说:“我们组考87分的人最多”,小华说:“我们组7位同学成绩排在最中间的恰好也是87分”上面两位同学的话能反映出的统计量是( )
A.众数和平均数 B.平均数和中位数 C.众数和方差 D.众数和中位数
15.某地原有沙漠108公顷,绿洲54公顷,为改善生态环境,防止沙化现象,当地政府实施了沙漠变绿洲”工程,要把部分沙漠改造为绿洲,使绿洲面积占沙漠面积的80%。设把x公顷沙漠改造为绿洲,则可列方程为( )
A.54+x=80%×108 B.54+x=80%(108-x) C. 54-x=80%(108+x) D. 108-x=80%(54+x)
16.已知AB,CD是⊙O的两条平行弦,AB=8,CD=6,⊙O的半径为5,则弦AB与CD的距离为( )
A.1 B.7 C.4或3 D.7或1
17.如图6,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交DB于点F,则△DEF的面积与△BAF的面积之比为( )
A. 1:3 B.3:4 C.1:9 D.9:16
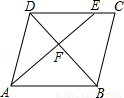

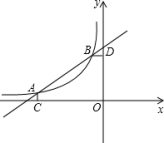
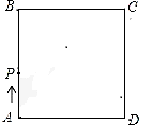
图6 图7 图8 图9
18.如图7,正方形ABCD的对角线相交于点O,Rt△OEF绕点O旋转,在旋转过程中,两个形重叠部分的面积是正方形面积的( )
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
19.如图8,已知A(-4,![]() )B(-1,2)是一次函数y1=kx+b(k≠0)与反比例函数为y2 =
)B(-1,2)是一次函数y1=kx+b(k≠0)与反比例函数为y2 =![]() (m≠0,x<0)图象的两个交点,AC⊥x轴于点C,BD⊥y轴于点D,若y1>y2,则x的值范围是( )
(m≠0,x<0)图象的两个交点,AC⊥x轴于点C,BD⊥y轴于点D,若y1>y2,则x的值范围是( )
A. x<-4 B.-4<x<-1 C. x<-4或x>-1 D.x<-1
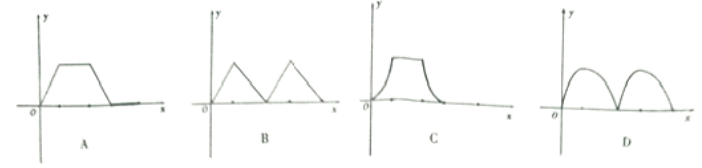
20.如图9,在矩形ABCD中,点P从点A出发,沿着矩形的边顺时针方向运动一周回到点A. 则点A、P、D围成的图形面积y与点P运动路程x之间形成的函数关系式的大致图象( )
三、(本大题共3小题,第21题5分,第22题5分,第23题7分,共17分)
21.计算:(3-![]() )°- 6cos30 +
)°- 6cos30 +![]() -(
-( ![]() )-1
)-1
22.解分式方程:![]() = 1
= 1
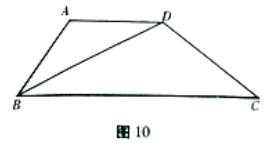
23.如图10,在四边形ABCD中,AB=AD,AD//BC.
(1)在图中,用尺规作线段BD的垂直平分线EF,分别交BD、BC于点E、F.(保留作图痕迹,不写作法)(2)连接DF,证明四边形ABFD为菱形.
24.(本小题满分9分)某地图书馆为了满足群众多样化阅读的需求,决定购买甲、乙两种品牌的电脑若干台组建电子阅览室.经了解,甲、乙两种品牌的电脑单价分别为3100元和4600.(1)若购买甲、乙两种品牌的电脑共50台,恰好支出200000元,求甲、乙两种品牌的电脑各购买了多少台?(2)若购买甲、乙两种品牌的电脑共50台,每种品牌至少购买一台,且支出不超过160000元,共有几种购买方案?并说明哪种方案最省钱?
25.(本小题满分9分)
如图,在△ABC中,∠ABC=90°,以AB为直径作⊙O交AC于D,点E在BC边上,且满足EB=ED.
(1)求证:DE是⊙O的切线;
(2)连接AE,若∠C=45°,AB=10![]() ,求sin∠CAE的值.
,求sin∠CAE的值. 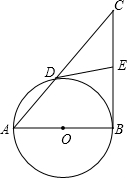
26.某批彩色弹力球的质量检验结果如下表
抽取的彩色弹力球数n | 500 | 1000 | 1500 | 2000 | 2500 |
优等品频数m | 471 | 946 | 1426 | 1898 | 2370 |
优等品频率 | 0.942 | 0.946 | 0.951 | 0.949 | 0.948 |
(1)请在图12中完成这批彩色弹力球“优等品”频率的折线统计图
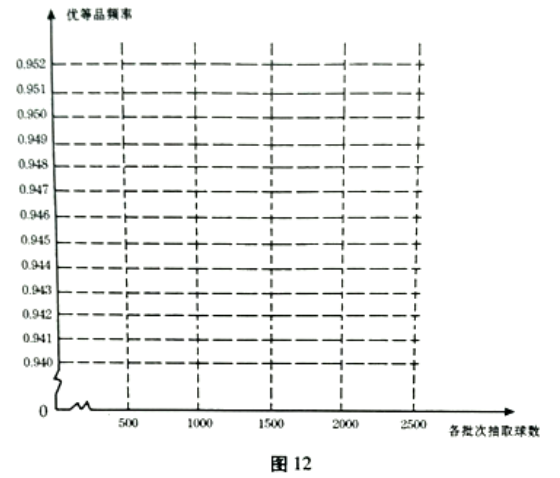
(2)这批彩色弹力球“优等品”概率的估计值大约是多少?(精确到0.01)
(3)从这批彩色弹力球中选择5个黄球、13个黑球、22个红球,它们除了颜色外都相同,将它们放入一个不透明的袋子中,求从袋子中摸出一个球是黄球的概率.
(4)现从第(3)问所说的袋子中取出若干个黑球,并放入相同数量的黄球,搅拌均匀,使从
袋子中摸出一个黄球的概率为![]() ,求取出了多少个黑球?
,求取出了多少个黑球?
五、(本大题共2小题,第27题11分,第28题12分,共23分)
27.请完成如下探究系列的有关问题:探究1:如图13-1,△ABC是等腰直角三角形,∠BAC=90°°,点D为BC上一动点,连接AD,以AD为边在AD的右侧作正方形ADEF,连接CF.则线段CF,BD之间的位置关系为_____,数量关系为_____.
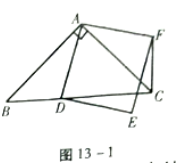
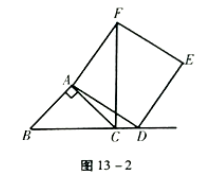
探究2:如图13-2,当点D运动到线段BC的延长线上,其余条件不变,探究1中的两条论是否仍然成立?为什么?(请写出证明过程)
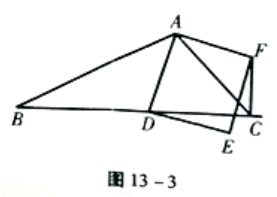
探究3:如图13-3,如果AB≠AC,∠BAC≠90°,∠BCA仍然保留为45°,点D在线段BC上运动,请你判断线段CF,BD之间的位置关系,并说明理由.
28.如图14,抛物线y=![]() x2-
x2- ![]() x-2与x轴交于A,B两点,与y轴交于点C,点D与点C关于x轴对称.
x-2与x轴交于A,B两点,与y轴交于点C,点D与点C关于x轴对称.
(1)求点A、B、C的坐标.
(2)求直线BD的解析式.
(3)在直线BD下方的抛物线上是否存在一点P,使△PBD的面积最大?若存在,求出点P的坐标;若不存在,请说明理由.





2019年青海省中考数学试卷与答案: 这是一份2019年青海省中考数学试卷与答案,共12页。试卷主要包含了填空题,单项选择题等内容,欢迎下载使用。
2019年青海省中考数学试卷及答案: 这是一份2019年青海省中考数学试卷及答案,共7页。试卷主要包含了填空题,单项选择题等内容,欢迎下载使用。
2018年青海省中考数学试卷与答案: 这是一份2018年青海省中考数学试卷与答案,共12页。试卷主要包含了填空题.,单项选择题.等内容,欢迎下载使用。












