
2022-2023学年福建省泉州市安溪县八年级(下)期末数学试卷(含解析)
展开2022-2023学年福建省泉州市安溪县八年级(下)期末数学试卷
一、选择题(本大题共10小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
1. 20230等于( )
A. 2023 B. 12023 C. 1 D. 0
2. PM2.5是指大气中直径小于等于2.5微米,即0.0000025米的颗粒物,将0.0000025用科学记数法表示为( )
A. 2.5×10−7 B. 2.5×10−6 C. 25×10−7 D. 0.25×10−6
3. 在平面直角坐标系中,点(4,−3)关于x轴对称的点的坐标是( )
A. (4,3) B. (4,−3) C. (−4,3) D. (−4,−3)
4. 将直线y=−2x+1向下平移3个单位长度得到直线l,则直线l的解析式为( )
A. y=−5x+1 B. y=−2x+4 C. y=−2x−2 D. y=2x−2
5. 在▱ABCD中,∠A:∠B=5:1,则∠D的度数为( )
A. 30° B. 60° C. 120° D. 150°
6. 下列条件中,能够判定▱ABCD为矩形的是( )
A. AB=BC B. AC⊥BD C. AC=BD D. AB=AC
7. 一组数据的方差计算公式为s2=14[(8−x−)2+(8−x−)2+(9−x−)2+(11−x−)2],下列关于这组数据的说法错误的是( )
A. 平均数是9 B. 中位数是8.5 C. 众数是8 D. 方差是1
8. 如图,正方形ABCD的面积为2,菱形AMCN的面积为1,则M,N两点间的距离为( )
A. 1
B. 2
C. 2
D. 3
9. 如图,在同一平面直角坐标系中,函数y=kx和y=−kx+2(k≠0)的大致图象可能是( )
A. B. C. D.
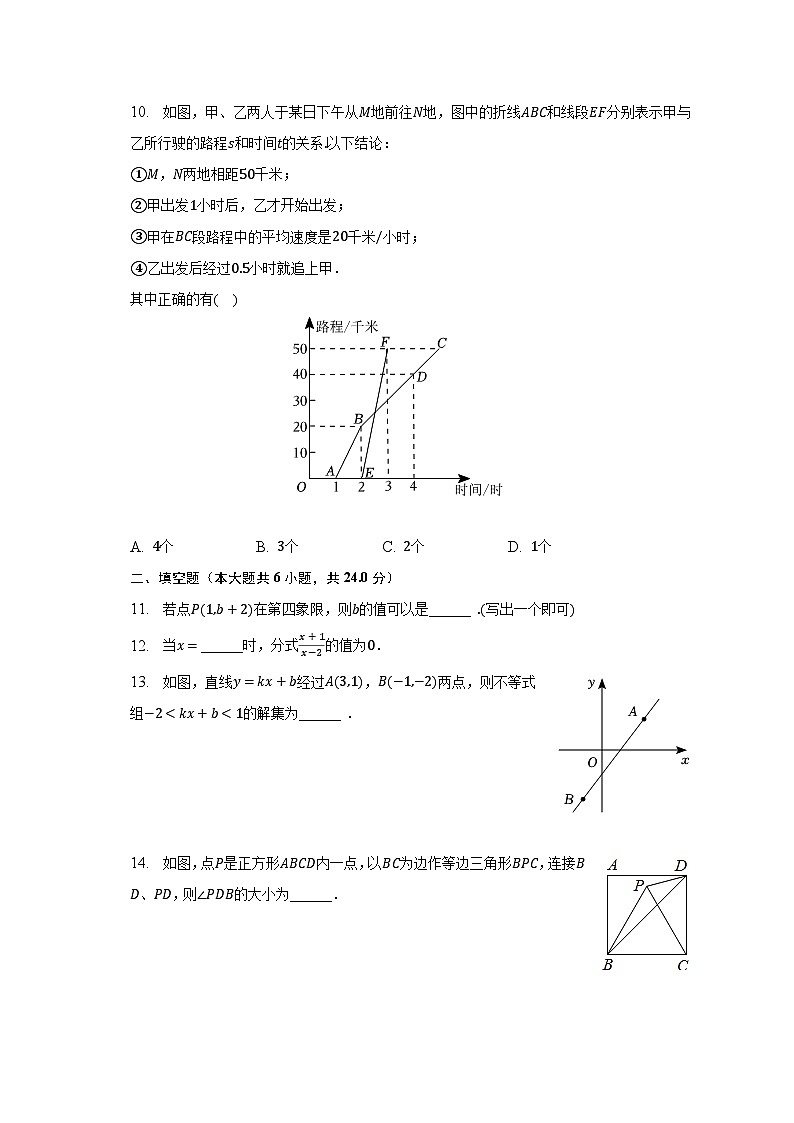
10. 如图,甲、乙两人于某日下午从M地前往N地,图中的折线ABC和线段EF分别表示甲与乙所行驶的路程s和时间t的关系.以下结论:
①M,N两地相距50千米;
②甲出发1小时后,乙才开始出发;
③甲在BC段路程中的平均速度是20千米/小时;
④乙出发后经过0.5小时就追上甲.
其中正确的有( )
A. 4个 B. 3个 C. 2个 D. 1个
二、填空题(本大题共6小题,共24.0分)
11. 若点P(1,b+2)在第四象限,则b的值可以是______ .(写出一个即可)
12. 当x=______时,分式x+1x−2的值为0.
13. 如图,直线y=kx+b经过A(3,1),B(−1,−2)两点,则不等式组−2
14. 如图,点P是正方形ABCD内一点,以BC为边作等边三角形BPC,连接BD、PD,则∠PDB的大小为______.
15. 已知点P(a,3b2−3),且实数a,b满足a−4b2+8=0,则点P到原点的最短距离为______ .
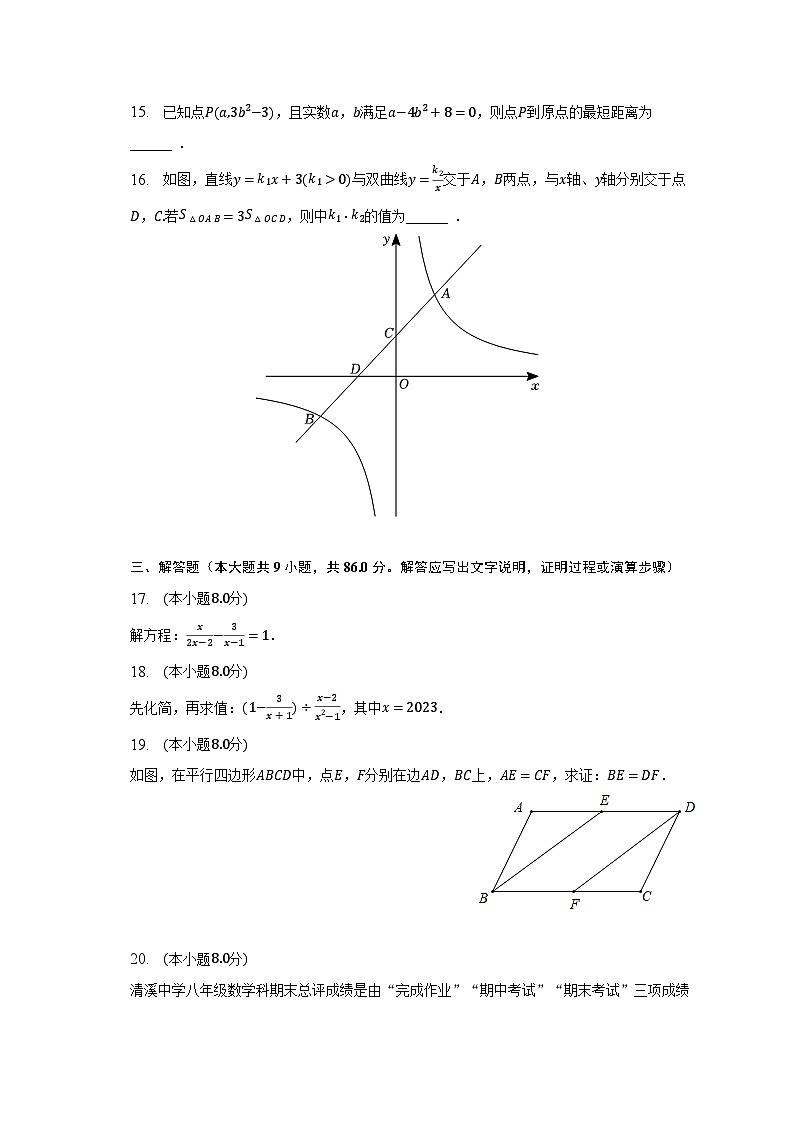
16. 如图,直线y=k1x+3(k1>0)与双曲线y=k2x交于A,B两点,与x轴、y轴分别交于点D,C.若S△OAB=3S△OCD,则中k1⋅k2的值为______ .
三、解答题(本大题共9小题,共86.0分。解答应写出文字说明,证明过程或演算步骤)
17. (本小题8.0分)
解方程:x2x−2−3x−1=1.
18. (本小题8.0分)
先化简,再求值:(1−3x+1)÷x−2x2−1,其中x=2023.
19. (本小题8.0分)
如图,在平行四边形ABCD中,点E,F分别在边AD,BC上,AE=CF,求证:BE=DF.
20. (本小题8.0分)
清溪中学八年级数学科期末总评成绩是由“完成作业”“期中考试”“期末考试”三项成绩组成的,如果期末总评成绩80分以上,则评为“优秀”.下面表中是小安和小溪两位同学的成绩记录:(8分)
完成作业
期中考试
期末考试
小安
70
90
80
小溪
75
72
(1)若按三项成绩的平均分记为期末总评成绩,请计算小安的期末总评成绩;
(2)若完成作业、期中考试、期末考试三项成绩按2:3:5的权重来确定期末总评成绩,则小溪在期末考试(期末成绩为整数)至少考多少分才能达到优秀?
21. (本小题8.0分)
如图,在平面直角坐标系中,直线y=23x+2与双曲线y=kx(k>0)交于点A(a,4),与x轴交于点B.
(1)求k的值;
(2)过点A的直线交x轴正半轴于点D,当△ABD是以BD为底边的等腰三角形时,求直线AD所对应一次函数的解析式.
22. (本小题10.0分)
如图,在△ABC中,点D在AC上,过点D作DE//BC交AB于点E.
(1)求作过点D且平行于AB的直线,交BC于点F(要求:尺规作图,不写作法,保留作图痕迹);
(2)在(1)的条件下,若BD平分∠ABC,求证:四边形BFDE为菱形.
23. (本小题10.0分)
湖头米粉和官桥豆干是安溪的两大特产.已知一箱湖头米粉比一箱官桥豆干的价格高30元,且用400元购买湖头米粉的箱数和用250元购买官桥豆于的箱数相等.
(1)求湖头米粉、官桥豆干每箱各多少元?
(2)若要购进湖头米粉和官桥豆干共60箱,且湖头米粉的箱数不少于官桥豆干的箱数的2倍.试求购买这两种特产总费用的最小值.
24. (本小题12.0分)
如图,点E在正方形ABCD的边AB上(不与点A,B重合),作点D关于直线CE的对称点D′.DD′与BC相交于点F,连接D′B并延长,交CE的延长线于点G.
(1)求证:CE=DF;
(2)求证:∠G=45°.
25. (本小题14.0分)
如图1,直线l1:y=x+b1分别与x轴、y轴交于点A,B,直线l2:y=−12x+b2分别与y轴、x轴交于点C,D,l1,l2的交点G在第一象限,且b2>b1>0,3OA=2BC.
(1)求b1,b2满足的关系式;
(2)若四边形BODG的面积为22.
①点E,F分别在x轴、直线l2上,当以B,G,E,F为顶点的四边形是平行四边形时,求点F的坐标;
②如图2,正方形BMNG中,顶点M在x轴的正半轴上,同时正方形B′M′N′G′的两个顶点N′,G′在反比例函数y=kx的图象上,另两个顶点B′,M′分别在y轴、x轴的正半轴上.当k的值改变时,正方形B′M′N′G′的大小也随之改变,若变化的正方形B′M′N′G′与正方形BMNG有重叠部分时,直接写出k的取值范围.
答案和解析
1.【答案】C
【解析】解:20230=1.
故选:C.
零指数幂:a0=1(a≠0),由此即可得到答案.
本题考查零指数幂,关键是掌握零指数幂:a0=1(a≠0).
2.【答案】B
【解析】解:0.0000025=2.5×10−6,
故选:B.
绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10−n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
本题考查用科学记数法表示较小的数,一般形式为a×10−n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定,掌握表示方法是解题关键.
3.【答案】A
【解析】解:点(4,−3)关于x轴的对称点的坐标是(4,3).
故选:A.
根据关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数;即点(x,y)关于x轴的对称点的坐标是(x,−y)即可得到点(4,3)关于x轴对称的点的坐标.
本题主要考查了关于x轴、y轴对称的点的坐标规律,掌握关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数.关于y轴对称点的坐标特点:横坐标互为相反数,纵坐标不变是关键.
4.【答案】C
【解析】解:由“上加下减”的原则可知,将直线y=−2x+1向下平移3个单位长度得到直线l,则直线l的解析式为:y=−2x+1−3,即y=−2x−2.
故选:C.
直接根据“上加下减”的原则进行解答即可.
本题考查的是一次函数的图象与几何变换,熟知“上加下减,左加右减”的原则是解答此题的关键.
5.【答案】A
【解析】解:在平行四边形ABCD中,∠A:∠B:=5:1,∠A+∠B=180°,∠B=∠D,
设∠A=5x,则∠B=x,
∴5x+x=180°,
∴x=30°,
∴∠D=∠B=30°,
故选:A.
设∠A=5x,则∠B=x,根据“平行四边形的对角相等,邻角互补”列出方程进而解答即可.
本题考查了平行四边形的性质,难度不大,注意熟练掌握平行四边形的性质是关键.
6.【答案】C
【解析】解:∵▱ABCD中,AB=BC,
∴▱ABCD是菱形,
故选项A不符合题意;
∵▱ABCD中,AC⊥BD,
∴▱ABCD是菱形,
故选项B不符合题意;
∵▱ABCD中,AC=BD,
∴▱ABCD是矩形,
故选项C符合题意;
▱ABCD中,AB=AC,不能判定▱ABCD是矩形,
故选项D不符合题意;
故选:C.
由矩形的判定和菱形的判定分别对各个选项进行判断即可.
本题考查了矩形的判定、菱形的判定、平行四边形的性质等知识,熟练掌握矩形的判定和菱形的判定是解题的关键.
7.【答案】D
【解析】解:由方差的计算公式知,这组数据为8、8、9、11,
所以这组数据的平均数为8+8+9+114=9,中位数为8+92=8.5,众数为8,
方差s2=14[(8−9)2+(8−9)2+(9−9)2+(11−9)2]=32,
故选:D.
由方差的计算公式知,这组数据为8、8、9、11,再根据方差、众数、中位数及平均数的定义求解即可.
本题主要考查方差,解题的关键是掌握方差、众数、中位数及平均数的定义.
8.【答案】A
【解析】解:连接AC交MN于O,如图:
∵正方形ABCD的面积为2,
∴12AC2=2,
∴AC=2,
∵菱形AMCN的面积为1,
∴12AC⋅MN=1,
∴12×2⋅MN=1,
∴MN=1;
故选:A.
连接AC交MN于O,由正方形ABCD的面积为2,求得AC=2,又菱形AMCN的面积为1,故12×2⋅MN=1,从而可得MN=1.
本题考查正方形性质和菱形的性质,解题的关键是掌握正方形面积,菱形的面积公式.
9.【答案】D
【解析】解:当k>0时,y=−kx+2k过一、二、四象限;
y=kx图象在一、三象限;
当k<0时,y=−kx+2k过一、二、二象限;
y=kx图象在二、四象限,
故选:D.
令k>0和k<0,分别找出函数图象所过象限,能共存者即为正确答案.
本题考查了反比例函数与一次函数的图象,熟悉函数的性质是解题的关键.
10.【答案】B
【解析】解:由图象可知,MN两地路程为50km,
∴①正确;
∵甲在1时出发,乙在2时出发,2−1=1小时,
∴②正确;
∵甲在BC段2小时行驶的路程为40−20=20km,
∴甲在BC段路程中的平均速度为20÷2=10千米/时,
∴③错误;
设乙出发t小时追上了甲,根据题意得,
20+10t=50t,
解得t=0.5,
∴④正确.
故选B.
由图象可知,MN两地路程为50km,故①正确;甲在1时出发,乙在2时出发,故②正确;根据甲在BC段2小时行驶的路程为40−20=20km,可得甲在BC段路程中的平均速度为10千米/时,故③错误;设乙出发t小时追上了甲,根据题意得20+10t=50t,解得t=0.5,故④正确.即可得解.
本题考查了函数图象,一元一次方程的应用,从图象中获取正确的信息是解题的关键.
11.【答案】−3
【解析】解:∵第四象限内点的坐标特征为横坐标是正,纵坐标是负,
∴b+2<0,
解得b<−2,
∴b的值可以是−3,答案不唯一,
故答案为−3.
根据第四象限内点的坐标特征为横坐标是正,纵坐标是负,判断点P的纵坐标b+2<0,解得b<−2,写出一个符合条件的解即可.
本题考查的是坐标系中点的坐标特征,熟练掌握坐标系中每个象限的坐标特征是解题关键.
12.【答案】−1
【解析】解:由分式的值为零的条件得x+1=0,且x−2≠0,
解得:x=−1,
故答案为:−1.
根据分式值为零的条件得x+1=0且x−2≠0,再解方程即可.
此题主要考查了分式值为零的条件,关键是掌握分式值为零的条件是分子等于零且分母不等于零.
13.【答案】−1
∴关于x的不等式−2
14.【答案】30°
【解析】解:∵四边形ABCD是正方形,
∴∠ABC=∠BCD=90°,BC=CD,
∵△BPC是等边三角形,
∴∠PBC=∠BCP=∠BPC=60°,BP=PC=BC,
∵BC=CD,∠BCD=90°,
∴∠DBC=45°,
∴∠PBD=∠PBC−∠DBC=60°−45°=15°,
∵∠BCD=90°,∠BCP=60°,
∴∠PCD=90°−60°=30°,
∵PD=DC,
∴∠DPC=180°−30°2=75°,
∴∠PDB=180°−∠PBD−∠BPC−∠CPD=180°−15°−60°−75°=30°,
故答案为:30°.
根据正方形的性质和等边三角形的性质得出∠DPC=75°,进而解答即可.
此题考查正方形的性质,关键是根据正方形的性质和三角形的内角和定理解答.
15.【答案】125
【解析】解:设原点为O,
∵a−4b2+8=0,
∴a=4b2−8,
∵P(a,3b2−3),
∴OP2=a2+(3b2−3)2,
即OP2=(4b2−8)2+(3b2−3)2
=25b4−82b2+73
=25(b2−1125)2+14425,
∴当b2=1125时,OP2有最小值为14425,
∴OP的最小值为125,
即点P到原点的最短距离为125,
故答案为:125.
设原点为O,用含b的代数式表示a,根据两点间的距离公式得出OP2=(4b2−8)2+(3b2−3)2化成完全平方的形式即可求解.
本题考查了勾股定理,两点间的距离公式,熟练掌握两点间的距离公式是解题的关键.
16.【答案】18
【解析】解:∵直线y=k1x+3(k1>0)与y轴交于点C,
∴C(0,3),
∵直线y=k1x+3(k1>0)与x轴交于点D,
∴D(−3k1,0),
∴S△OCD=12×OD×OC=12×3k1×3=92k1,
设A(m1,n1),B(m2,n2),
令k1x+3=k2x,整理得:k1x2+3x−k2=0,
由根与系数的关系得:m1+m2=−3k1,m1m2=−k2k1,
S△AOB=S△AOC+S△BOC=12×OC(m1−m2)=32(m1−m2),
∵m1−m2= (m1+m2)2−4m1m2= 9k12+4×k2k1,
∴S△AOB=32 9k12+4×k2k1,
又∵S△OAB=3S△OCD,
∴32 9k12+4×k2k1=3×92k1,
整理得:
9k12+4k2k1=81k12,
∴9+4k1k2=81,
∴k1k2=18.
故答案为:18.
设出点A、B的坐标,求出点C的坐标,利用面积的等量关系建立关于k1k2的方程即可求出它们的积.
本题考查反比例函数与一次函数图象交点坐标,把点的坐标代入是求函数关系式常用的方法,将坐标转化为线段的长是正确解答的关键.
17.【答案】解:去分母得:x−6=2x−2,
移项得:x−2x=6−2,
合并化系数得:x=−4.
检验:将x=−4代入2(x−1)=−10≠0.符合题意.
∴x=−4.
【解析】根据解分式方程的步骤进行运算即可.
本题考查了解分式方程,分式方程的解需要检验.
18.【答案】解:(1−3x+1)÷x−2x2−1
=x+1−3x+1⋅(x+1)(x−1)x−2
=x−2x+1⋅(x+1)(x−1)x−2
=x−1,
当x=2023时,原式=2023−1=2022.
【解析】先利用异分母分式加减法法则计算括号里,再算括号外,然后把x的值代入化简后的式子进行计算,即可解答.
本题考查了分式的化简求值,准确熟练地进行计算是解题的关键.
19.【答案】证明:∵四边形ABCD是平行四边形
∴AD=BC,AD//BC,
∵AE=CF,
∴DE=BF,
又∵DE//BF,
∴四边形BEDF是平行四边形,
∴BE=DF.
【解析】先求出DE=BF,再证明四边形BEDF是平行四边形,即可得出结论.
本题考查了平行四边形的判定与性质;熟练掌握平行四边形的判定方法,证明四边形是平行四边形是解决问题的关键.
20.【答案】解:(1)小安的期末总评成绩为:70+90+803=80(分);
(2)设小溪在期末考试(期末成绩为整数)至少考x分才能达到优秀,则:
75×2+72×3+5x2+3+5≥80,
解得x≥86.8,
答:至少考86.8分才能达到优秀.
【解析】(1)直接利用算术平均数的计算公式计算即可;
(2)利用加权平均数的计算公式进行计算即可.
本题考查的是加权平均数的求法.熟记公式是解决本题的关键.解题时要认真审题,不要把数据代错.
21.【答案】解:(1)∵一次函数y=23x+2的图象经过点A(a,4),
∴23a+2=4,
解得:a=3,
∴A(3,4),
将A(3,4)代入y=kx(k>0),
得:4=k3,
∴k=12
(2)如图,过点A作AE⊥x轴于点E,
在y=23x+2中,
令y=0,
得23x+2=0,
解得:x=−3,
∴B(−3,0),
∵E(3,0),
∴BE=3−(−3)=6,
∵△ABD是以BD为底边的等腰三角形,
∴AB=AD,
∵AE⊥BD,
∴DE=BE=6,
∴D(9,0),
设直线AD的函数表达式为y=mx+n,
∵A(3,4),D(9,0),
∴3m+n=49m+n=0,
解得m=−23n=6,
∴直线AD的函数表达式为y=−23x+6.
【解析】(1)根据一次函数y=23x+2 的图象经过点A(a,4),求出点A的坐标,再代入y=kx(k>0),即可求得答案;
(2)过点A作AE⊥x轴于点E,先求出点B的坐标,再根据△ABD是以BD为底边的等腰三角形,可求出点D的坐标,利用待定系数法即可求出直线AD的解析式.
本题考查反比例函数的综合应用,掌握待定系数法求函数解析式,一次函数图象与坐标轴的交点,一次函数图象与反比例函数图象的交点问题是解题的关键.
22.【答案】(1)解:如图所示;
(2)证明:∵DE//BC,DF//AB,
∴四边形BFDE是平行四边形,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵DE//BC,
∴∠EBD=∠CBD,
∴∠ABD=∠EBD,
∴BE=DE,
∴四边形BFDE是菱形.
【解析】(1)作∠BDF=∠ABD,根据平行线的判定可求解;
(2)利用平行四边形的定义可证明四边形BFDE是平行四边形,再根据平行线的性质及角平分线的定义可得∠ABD=∠EDB,即可证得BE=ED,进而可证明结论.
本题主要考查尺规作图,平行线的判定,等腰三角形的性质,菱形的判定,掌握菱形的判定条件是解题的关键.
23.【答案】解:(1)设官桥豆干的价格是x元/箱,则湖头米粉的价格是(x+30)元/箱,
根据题意得:400x+30=250x,
解得:x=50,
经检验,x=50是所列方程的解,且符合题意,
∴x+30=50+30=80.
答:湖头米粉的价格是80元/箱,官桥豆干的价格是50元/箱;
(2)设购进湖头米粉m箱,则购进官桥豆干(60−m)箱,
根据题意得:m≥2(60−m),
解得:m≥40.
设购买这两种特产总费用为w元,则w=80m+50(60−m),
即w=30m+3000,
∵30>0,
∴w随m的增大而增大,
∴当m=40时,w取得最小值,最小值=30×40+3000=4200.
答:购买这两种特产总费用的最小值为4200元.
【解析】(1)设官桥豆干的价格是x元/箱,则湖头米粉的价格是(x+30)元/箱,利用数量=总价÷单价,结合用400元购买湖头米粉的箱数和用250元购买官桥豆于的箱数相等,可列出关于x的分式方程,解之经检验后,可得出官桥豆干的价格,再将其代入(x+30)中,即可求出湖头米粉的价格;
(2)设购进湖头米粉m箱,则购进官桥豆干(60−m)箱,根据购进湖头米粉的箱数不少于官桥豆干的箱数的2倍,可列出关于m的一元一次不等式,解之可求出m的取值范围,设购买这两种特产总费用为w元,利用总价=单价×数量,可得出w关于m的函数关系式,再利用一次函数的性质,即可解决最值问题.
本题考查了分式方程的应用、一元一次不等式的应用以及一次函数的应用,解题的关键是:(1)找准等量关系,正确列出分式方程;(2)根据各数量之间的关系,找出w关于m的函数关系式.
24.【答案】(1)证明:∵四边形ABCD是正方形,
∴BC=CD,∠EBC=∠FCD=90°,
∴∠DCH+∠BCE=90°,
∵点D关于直线CE的对称点是D′,
∴CE⊥DD′,
∴∠CHD=90°,
∴∠DCH+∠CDF=90°,
∴∠BCE=∠CDF,
在△BCE和△CDF中,
∠BCE=∠CDFBC=CD∠EBC=∠FCD,
∴△BCE≌△CDF(ASA),
∴CE=DF;
(2)证明:连接CD′,
∵点D关于直线CE的对称点是D′,
∴CE⊥DD′,CD=CD′,
∴∠D′HG=90°,∠CDF=∠CD′D,
∵四边形ABCD是正方形,
∴CD=CB,
∴CB=CD′,
∴∠CBD′=∠CD′B,
∵∠CBD′是△CBG的一个外角,
∴∠CBD′=∠G+∠BCE,
∵∠CD′B=∠HD′G+∠CD′D,∠CDF=∠CD′D,
∴∠CD′B=∠HD′G+∠CDF,
由(1)知∠BCE=∠CDF,
∴∠G=∠HD′G,
又∠D′HG=90°,
∴∠G=45°.
【解析】(1)根据轴对称的性质得出CE⊥DD′,再根据同角的余角相等得出∠BCE=∠CDF,最后证得△BCE和△CDF全等,即可得出结论;
(2)根据轴对称的性质得出CE⊥DD′,CD=CD′,结合正方形的性质得出CB=CD′,于是有∠CBD′=∠CD′B,根据∠CBD′=∠G+∠BCE,∠CD′B=∠HD′G+∠CDF,即可得出∠G=45°.
本题考查了正方形的性质,三角形全等的判定与性质,轴对称的性质,熟练掌握这些性质是解题的关键.
25.【答案】解:(1)∵直线l1:y=x+b1与x轴、y轴交于点A、B,直线l2:y=−12x+b2与y轴交于点C,
∴A(−b1,0),B(0,b1),C(0,b2),
∴OA=b1,OC=b2,BC=b2−b1,
∵3OA=2BC,
∴3b1=2(b2−b1),
∴b2=52b1;
(2)①∵直线l2:y=−12x+b2分别与x轴交于点D,
∴D(2b2,0),
∴OD=2b2,
∵l1,l2的交点G在第一象限,
∴−12x+b2=x+b1,
解得:xG=23(b2−b1),
∵四边形BODG的面积为22,
∴S△CDO−S△BCG=22,
∴12OD⋅OC−12BC⋅xG=22,
即12×2b2×b2−12(b2−b1)×23(b2−b1)=22,
化简得:b22−13(b2−b1)2=22,
又∵b2=52b1,b2>b1>0,
∴b1=2,b2=5,
∴直线l1的解析式为y=x+2,直线l2的解析式为y=−12x+5,
∴B(0,2),G(2,4),
∵点E,F分别在x轴、直线l2上,
∴设E(e,0),F(f,−12f+5),
当EF、BG为对角线时,则EF、BG的中点重合,
∴e+f=0+20−12f+5=2+4,
解得:e=4f=−2,
∴F(−2,6);
当EG、BF为对角线时,则EG、BF的中点重合,
∴e+2=0+f0+4=2−12f+5,
解得:e=4f=6,
∴F(6,2);
当EB、FG为对角线时,则EB、FG的中点重合,
∴e+0=f+20+2=−12f+5+4,
解得:e=16f=14,
∴F(14,−2);
综上所述,点F的坐标为(−2,6)或(6,2)或(14,−2);
②设G′(a,ka),N′(b,kb),
则EG′=a,OE=ka,FN′=kb,OF=b,G′H=b−a,
过点G′作G′E⊥y轴于点E,过点N′作N′F⊥x轴于点F,EG′与FN′交于点H,如图,
则∠B′EG′=∠H=∠M′FN′=∠B′OM′=90°,
∴∠EB′G′+∠EG′B′=∠HG′N′+∠HN′G′=∠FM′N′+∠FN′M′=∠OB′M′+∠OM′B′=90°,
∵四边形B′M′N′G′是正方形,
∴B′M′=M′N′=N′G′=B′G′,∠G′B′M′=∠B′M′N′=∠M′N′G′=∠B′G′N′=90°,
∴∠EB′G′+∠OB′M′=∠EG′B′+∠HG′N′=∠HN′G′+∠FN′M′=∠FM′N′+∠OM′B′=90°,
∴∠EB′G′=∠OM′B′=∠FN′M′=∠HG′N′,
∴△EB′G′≌△OM′B′≌△FN′M′≌△HG′N′(AAS),
∴B′E=OM=FN′=G′H,EG′=HN′=FM′=OB′,
∴b−a=kbka−a=kb,
解得:b=2a,
∴OM′=FM′=OB′=B′E=EG′=HG′=HN′=a,
∴△OB′M′为等腰直角三角形,
∴∠B′M′O=45°,G′(a,2a),N′(2a,a),B(0,a),
∵B(0,2),G(2,4),M(2,0),N(4,2),
∴直线BM、GN的解析式分别为y=−x+2和y=−x+6,
当G′N′在BM边上时,如图,
把G′(a,2a)代入y=−x+2,得:2a=−a+2,
解得:a=23,
∴G′(23,43),
∴k=23×43=89;
当B′M′与直线GN重合时,如图,
把B(0,a)代入y=−x+6,得:a=6,
∴G′(6,12),
∴k=6×12=72;
∴当正方形B′M′N′G′与正方形BMNG有重叠部分时,89≤k≤72.
【解析】(1)先求得:A(−b1,0),B(0,b1),C(0,b2),可得OA=b1,BC=b2−b1,由题意可得3b1=2(b2−b1),即b2=52b1;
(2)①先求得D(2b2,0),即OD=2b2,联立得−12x+b2=x+b1,可得xG=23(b2−b1),由三角形面积公式可得12OD⋅OC−12BC⋅xG=22,即12×2b2×b2−12(b2−b1)×23(b2−b1)=22,再结合b2=52b1,b2>b1>0,可得b1=2,b2=5,进而可得直线l1的解析式为y=x+2,直线l2的解析式为y=−12x+5,设E(e,0),F(f,−12f+5),分三种情况:当EF、BG为对角线时,则EF、BG的中点重合,当EG、BF为对角线时,则EG、BF的中点重合,当EB、FG为对角线时,则EB、FG的中点重合,分别求得点F的坐标即可;
②设G′(a,ka),N′(b,kb),过点G′作G′E⊥y轴于点E,过点N′作N′F⊥x轴于点F,EG′与FN′交于点H,可证得△EB′G′≌△OM′B′≌△FN′M′≌△HG′N′(AAS),得出B′E=OM=FN′=G′H,EG′=HN′=FM′=OB′,进而求得b=2a,利用待定系数法可得直线BM、GN的解析式分别为y=−x+2和y=−x+6,分两种情况:当G′N′在BM边上时,当B′M′与直线GN重合时,分别求得k的值,即可求得k的取值范围.
本题是反比例函数的综合题,考查K型全等的运用、等腰直角三角形的判定和性质,反比例函数系数k的几何意义.并要求学生掌握反比例函数比例系数|k|的大小和函数图象之间的关系.
2023-2024学年福建省泉州市安溪县八年级(上)期末数学试卷(含详细答案解析): 这是一份2023-2024学年福建省泉州市安溪县八年级(上)期末数学试卷(含详细答案解析),共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023-2024学年福建省泉州市安溪县八年级(上)期末数学试卷(含解析): 这是一份2023-2024学年福建省泉州市安溪县八年级(上)期末数学试卷(含解析),共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年福建省泉州市安溪县七年级(下)期末数学试卷(含解析): 这是一份2022-2023学年福建省泉州市安溪县七年级(下)期末数学试卷(含解析),共19页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。












