



高考数学真题分项汇编(全国通用)五年(2019-2023)专题03+导数及其应用(选填题)(理)
展开![]()
![]() 五年(2019-2023)年高考真题分项汇编
五年(2019-2023)年高考真题分项汇编
专题03 导数及应用(选填题)
![]()
函数导数应用是高考必考知识点

![]()
考点01 利用导数求函数单调性,极值最值
一、单选题
1.(2023年全国新高考Ⅱ卷)已知函数![]() 在区间
在区间![]() 上单调递增,则a的最小值为( ).
上单调递增,则a的最小值为( ).
A.![]() B.e C.
B.e C.![]() D.
D.![]()
2.(2021年全国新高考Ⅰ卷)若过点![]() 可以作曲线
可以作曲线![]() 的两条切线,则( )
的两条切线,则( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.(2020年全国高考Ⅰ卷)函数![]() 的图像在点
的图像在点![]() 处的切线方程为( )
处的切线方程为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
4.(2020年全国高考Ⅲ卷)若直线l与曲线y=![]() 和x2+y2=
和x2+y2=![]() 都相切,则l的方程为( )
都相切,则l的方程为( )
A.y=2x+1 B.y=2x+![]() C.y=
C.y=![]() x+1 D.y=
x+1 D.y=![]() x+
x+![]()
5.(2019年全国高考Ⅲ卷)已知曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题
6.(2023·全国乙卷)设![]() ,若函数
,若函数![]() 在
在![]() 上单调递增,则a的取值范围是______.
上单调递增,则a的取值范围是______.
7.(2022 全国乙卷)已知![]() 和
和![]() 分别是函数
分别是函数![]() (
(![]() 且
且![]() )的极小值点和极大值点.若
)的极小值点和极大值点.若![]() ,则a的取值范围是____________.
,则a的取值范围是____________.
8.(2022年全国新高考Ⅰ卷)若曲线![]() 有两条过坐标原点的切线,则a的取值范围是________________.
有两条过坐标原点的切线,则a的取值范围是________________.
9.(2021·全国甲卷)曲线![]() 在点
在点![]() 处的切线方程为__________.
处的切线方程为__________.
10.(2021年全国新高考Ⅰ卷)函数![]() 的最小值为______.
的最小值为______.
三、双空题
11.(2022年全国高考Ⅱ卷)曲线![]() 过坐标原点的两条切线的方程为____________,____________.
过坐标原点的两条切线的方程为____________,____________.
考点02 构造函数利用导数求单调性比较大小
![]()
![]() 一、单选题
一、单选题
1.(2022·全国甲卷)已知![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.(2022年全国新高考Ⅰ卷)设![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.(2021·全国乙卷)设![]() ,
,![]() ,
,![]() .则( )
.则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.(2020年全国新高考Ⅰ卷)若![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.(2020年全国高考Ⅱ卷)若![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.(2020年全国高考Ⅲ卷)已知55<84,134<85.设a=log53,b=log85,c=log138,则( )
A.a<b<c B.b<a<c C.b<c<a D.c<a<b
考点03 导数综合应用
1.(2020·天津·统考高考真题)已知函数![]() 若函数
若函数![]() 恰有4个零点,则
恰有4个零点,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2.(2022·天津·统考高考真题)设![]() ,对任意实数x,记
,对任意实数x,记![]() .若
.若![]() 至少有3个零点,则实数
至少有3个零点,则实数![]() 的取值范围为______.
的取值范围为______.
3.(2021·北京·统考高考真题)已知函数![]() ,给出下列四个结论:
,给出下列四个结论:
①若![]() ,
,![]() 恰 有2个零点;
恰 有2个零点;
②存在负数![]() ,使得
,使得![]() 恰有1个零点;
恰有1个零点;
③存在负数![]() ,使得
,使得![]() 恰有3个零点;
恰有3个零点;
④存在正数![]() ,使得
,使得![]() 恰有3个零点.
恰有3个零点.
其中所有正确结论的序号是_______.
4.(2019·江苏·高考真题)设![]() 是定义在
是定义在![]() 上的两个周期函数,
上的两个周期函数,![]() 的周期为4,
的周期为4,![]() 的周期为2,且
的周期为2,且![]() 是奇函数.当
是奇函数.当![]() 时,
时,![]() ,
,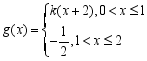 ,其中
,其中![]() .若在区间
.若在区间![]() 上,关于
上,关于![]() 的方程
的方程![]() 有8个不同的实数根,则
有8个不同的实数根,则![]() 的取值范围是_____.
的取值范围是_____.
高考数学真题分项汇编(全国通用)五年(2019-2023)专题05+立体几何(选填题)(文): 这是一份高考数学真题分项汇编(全国通用)五年(2019-2023)专题05+立体几何(选填题)(文),文件包含高考数学真题分项汇编五年2019-2023专题05立体几何选填题文科解析版docx、高考数学真题分项汇编五年2019-2023专题05立体几何选填题文科原卷版docx等2份试卷配套教学资源,其中试卷共46页, 欢迎下载使用。
高考数学真题分项汇编(全国通用)五年(2019-2023)专题04+导数及其应用(解答题)(理): 这是一份高考数学真题分项汇编(全国通用)五年(2019-2023)专题04+导数及其应用(解答题)(理),文件包含高考数学真题分项汇编五年2019-2023专题04导数及其应用解答题理科解析版docx、高考数学真题分项汇编五年2019-2023专题04导数及其应用解答题理科原卷版1docx等2份试卷配套教学资源,其中试卷共73页, 欢迎下载使用。
高考数学真题分项汇编(全国通用)五年(2019-2023)专题03+导数及其应用(选填题)(文): 这是一份高考数学真题分项汇编(全国通用)五年(2019-2023)专题03+导数及其应用(选填题)(文),文件包含高考数学真题分项汇编五年2019-2023专题03导数及其应用选填题文科解析版docx、高考数学真题分项汇编五年2019-2023专题03导数及其应用选填题文科原卷版docx等2份试卷配套教学资源,其中试卷共19页, 欢迎下载使用。













