

- 中考数学二轮精品专题复习 图形的相似 试卷 1 次下载
- 中考数学二轮精品专题复习 图形的平移 试卷 1 次下载
- 中考数学二轮精品专题复习 圆(解答题一) 试卷 1 次下载
- 中考数学二轮精品专题复习 四边形(选择题) 试卷 1 次下载
- 中考数学二轮精品专题复习 图形的对称 试卷 1 次下载
中考数学二轮精品专题复习 一次函数(选择题)
展开2023年中考数学真题知识点汇编之《一次函数(选择题)》
一.选择题(共19小题)
1.(2023•通辽)在平面直角坐标系中,一次函数y=2x﹣3的图象是( )
A. B.
C. D.
2.(2023•内蒙古)在平面直角坐标系中,将正比例函数y=﹣2x的图象向右平移3个单位长度得到一次函数y=kx+b(k≠0)的图象,则该一次函数的解析式为( )
A.y=﹣2x+3 B.y=﹣2x+6 C.y=﹣2x﹣3 D.y=﹣2x﹣6
3.(2023•长沙)下列一次函数中,y随x的增大而减小的函数是( )
A.y=2x+1 B.y=x﹣4 C.y=2x D.y=﹣x+1
4.(2023•无锡)将函数y=2x+1的图象向下平移2个单位长度,所得图象对应的函数表达式是( )
A.y=2x﹣1 B.y=2x+3 C.y=4x﹣3 D.y=4x+5
5.(2023•鄂州)象棋起源于中国,中国象棋文化历史悠久.如图所示是某次对弈的残图,如果建立平面直角坐标系,使棋子“帅”位于点(﹣2,﹣1)的位置,则在同一坐标系下,经过棋子“帅”和“马”所在的点的一次函数解析式为( )
A.y=x+1 B.y=x﹣1 C.y=2x+1 D.y=2x﹣1
6.(2023•兰州)一次函数y=kx﹣1的函数值y随x的增大而减小,当x=2时,y的值可以是( )
A.2 B.1 C.﹣1 D.﹣2
7.(2023•聊城)甲乙两地相距a千米,小亮8:00乘慢车从甲地去乙地,10分钟后小莹乘快车从乙地赶往甲地.两人分别距甲地的距离y(千米)与两人行驶时刻t(×时×分)的函数图象如图所示,则小亮与小莹相遇的时刻为( )
A.8:28 B.8:30 C.8:32 D.8:35
8.(2023•荆州)如图,直线y=−32x+3分别与x轴,y轴交于点A,B,将△OAB绕着点A顺时针旋转90°得到△CAD,则点B的对应点D的坐标是( )
A.(2,5) B.(3,5) C.(5,2) D.(13,2)
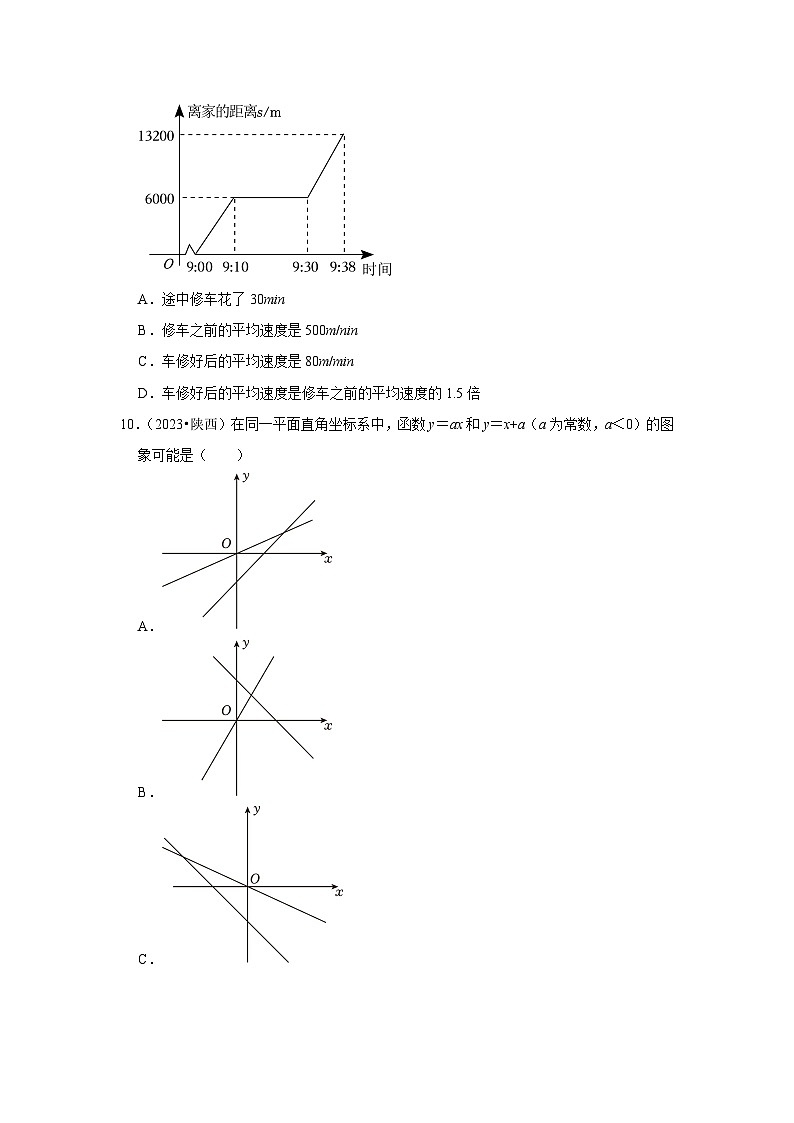
9.(2023•郴州)第11届中国(湖南)矿物宝石国际博览会在我市举行,小方一家上午9:00开车前往会展中心参观.途中汽车发生故障,原地修车花了一段时间.车修好后,他们继续开车赶往会展中心.以下是他们家出发后离家的距离s与时间的函数图象.分析图中信息,下列说法正确的是( )
A.途中修车花了30min
B.修车之前的平均速度是500m/nin
C.车修好后的平均速度是80m/min
D.车修好后的平均速度是修车之前的平均速度的1.5倍
10.(2023•陕西)在同一平面直角坐标系中,函数y=ax和y=x+a(a为常数,a<0)的图象可能是( )
A.
B.
C.
D.
11.(2023•随州)甲、乙两车沿同一路线从A城出发前往B城,在整个行程中,汽车离开A城的距离y与时刻t的对应关系如图所示,关于下列结论:①A,B两城相距300km;②甲车的平均速度是60km/h,乙车的平均速度是100km/h;③乙车先出发,先到达B城;④甲车在9:30追上乙车.正确的有( )
A.①② B.①③ C.②④ D.①④
12.(2023•乐山)下列各点在函数y=2x﹣1图象上的是( )
A.(﹣1,3) B.(0,1) C.(1,﹣1) D.(2,3)
13.(2023•金华)如图,两盏灯笼的位置A,B的坐标分别是(﹣3,3),(1,2),将点B向右平移2个单位,再向上平移1个单位得到点B′,则关于点A,B′的位置描述正确的是( )
A.关于x轴对称 B.关于y轴对称
C.关于原点O对称 D.关于直线y=x对称
14.(2023•山西)一种弹簧秤最大能称不超过10kg的物体,不挂物体时弹簧的长为12cm,每挂重1kg物体,弹簧伸长0.5cm,在弹性限度内,挂重后弹簧的长度y(cm)与所挂物体的质量x(kg)之间的函数关系式为( )
A.y=12﹣0.5x B.y=12+0.5x C.y=10+0.5x D.y=0.5x
15.(2023•临沂)对于某个一次函数y=kx+b(k≠0),根据两位同学的对话得出的结论,错误的是( )
A.k>0 B.kb<0 C.k+b>0 D.k=−12b
16.(2023•新疆)一次函数y=x+1的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
17.(2023•金昌)若直线y=kx(k是常数,k≠0)经过第一、第三象限,则k的值可为( )
A.﹣2 B.﹣1 C.−12 D.2
18.(2023•巴中)一次函数y=(k﹣3)x+2的函数值y随x增大而减小,则k的取值范围是( )
A.k>0 B.k<0 C.k>3 D.k<3
19.(2023•台湾)坐标平面上,一次函数y=﹣2x﹣6的图象通过下列哪一个点( )
A.(﹣4,1) B.(﹣4,2) C.(﹣4,﹣1) D.(﹣4,﹣2)
2023年中考数学真题知识点汇编之《一次函数(选择题)》
参考答案与试题解析
一.选择题(共19小题)
1.(2023•通辽)在平面直角坐标系中,一次函数y=2x﹣3的图象是( )
A. B.
C. D.
【考点】一次函数的图象.菁优网版权所有
【专题】一次函数及其应用;几何直观;推理能力.
【答案】D
【分析】根据一次函数y=2x﹣3中的k、b的符号确定其函数图象所经过的象限,即可判断.
【解答】解:∵一次函数y=2x﹣3中的k=2>0,b=﹣3<0,
∴一次函数y=2x﹣3的图象经过第一、三、四象限.
故选:D.
【点评】本题考查了一次函数图象与系数的关系,牢记“k>0,b<0⇔y=kx+b的图象在一、三、四象限”是解题的关键.
2.(2023•内蒙古)在平面直角坐标系中,将正比例函数y=﹣2x的图象向右平移3个单位长度得到一次函数y=kx+b(k≠0)的图象,则该一次函数的解析式为( )
A.y=﹣2x+3 B.y=﹣2x+6 C.y=﹣2x﹣3 D.y=﹣2x﹣6
【考点】一次函数图象与几何变换;一次函数的图象;正比例函数的图象.菁优网版权所有
【专题】一次函数及其应用;运算能力.
【答案】B
【分析】根据一次函数图象平移的规律解答即可.
【解答】解:正比例函数y=﹣2x的图象向右平移3个单位长度得到一次函数的解析式为y=﹣2(x﹣3)=﹣2x+6.
故选:B.
【点评】本题考查的是一次函数的图象与几何变换,熟知“上加下减,左加右减”是解题的关键.
3.(2023•长沙)下列一次函数中,y随x的增大而减小的函数是( )
A.y=2x+1 B.y=x﹣4 C.y=2x D.y=﹣x+1
【考点】正比例函数的性质;一次函数的性质.菁优网版权所有
【专题】一次函数及其应用;运算能力.
【答案】D
【分析】根据一次函数的增减性与系数的关系分别判断即可.
【解答】解:在一次函数y=2x+1中,
∵2>0,
∴y随着x增大而增大,
故A不符合题意;
在一次函数y=x﹣4中,
∵1>0,
∴y随着x增大而增大,
故B不符合题意;
在一次函数y=2x中,
∵2>0,
∴y随着x增大而增大,
故C不符合题意;
在一次函数y=﹣x+1中,
∵﹣1<0,
∴y随着x增大而减小,
故D符合题意,
故选:D.
【点评】本题考查了正比例函数的性质,一次函数的性质,熟练掌握这些性质是解题的关键.
4.(2023•无锡)将函数y=2x+1的图象向下平移2个单位长度,所得图象对应的函数表达式是( )
A.y=2x﹣1 B.y=2x+3 C.y=4x﹣3 D.y=4x+5
【考点】一次函数图象与几何变换.菁优网版权所有
【专题】一次函数及其应用;应用意识.
【答案】A
【分析】根据“上加下减”的平移规律解答即可.
【解答】解:将函数y=2x+1的图象向下平移2个单位长度,所得函数图象的表达式是y=2x+1﹣2=2x﹣1,
故选:A.
【点评】此题主要考查了一次函数图象与几何变换,求直线平移后的解析式时要注意平移时k的值不变,只有b发生变化.解析式变化的规律是:左加右减,上加下减.
5.(2023•鄂州)象棋起源于中国,中国象棋文化历史悠久.如图所示是某次对弈的残图,如果建立平面直角坐标系,使棋子“帅”位于点(﹣2,﹣1)的位置,则在同一坐标系下,经过棋子“帅”和“马”所在的点的一次函数解析式为( )
A.y=x+1 B.y=x﹣1 C.y=2x+1 D.y=2x﹣1
【考点】一次函数的应用.菁优网版权所有
【专题】一次函数及其应用;应用意识.
【答案】A
【分析】根据棋子“帅”位于点(﹣2,﹣1)的位置,求出“马”所在的点的坐标,由此解答即可.
【解答】解:∵“帅”位于点(﹣2,﹣1)可得出“马”(1,2),
设经过棋子“帅”和“马”所在的点的一次函数解析式为y=kx+b,
∴−1=−2k+b2=k+b,
解得k=1b=1,
∴y=x+1,
故选:A.
【点评】本题考查了一次函数的应用,掌握一次函数解析式的求法是解题的关键.
6.(2023•兰州)一次函数y=kx﹣1的函数值y随x的增大而减小,当x=2时,y的值可以是( )
A.2 B.1 C.﹣1 D.﹣2
【考点】一次函数图象上点的坐标特征;一次函数的性质.菁优网版权所有
【专题】一次函数及其应用;运算能力.
【答案】D
【分析】根据一次函数的性质,y随x的增大而减小k<0,分别计算各选项中y和x值下的k值,看哪个是负数,哪个就符合题意.
【解答】解:∵一次函数y=kx﹣1中,y随x的增大而减小,
∴k<0,
A、当x=2,y=2时,k=32,不符合题意;
B、当x=2,y=1时,k=1,不符合题意;
C、当x=2,y=﹣1时,k=0,不符合题意;
D、当x=2,y=﹣2时,k=−12,符合题意;
故选:D.
【点评】本题考查了一次函数的性质,开放型题目,所写函数解析式必须满足k<0.
7.(2023•聊城)甲乙两地相距a千米,小亮8:00乘慢车从甲地去乙地,10分钟后小莹乘快车从乙地赶往甲地.两人分别距甲地的距离y(千米)与两人行驶时刻t(×时×分)的函数图象如图所示,则小亮与小莹相遇的时刻为( )
A.8:28 B.8:30 C.8:32 D.8:35
【考点】一次函数的应用.菁优网版权所有
【专题】一次方程(组)及应用;运算能力.
【答案】A
【分析】设小亮与小莹相遇时,小亮乘车行驶了x小时,因为小亮、小莹乘车行驶的速度分别是67a千米/时,2a千米/时,即可得到方程:67ax+2a(x−16)=a,求出x的值,即可解决问题.
【解答】解:设小亮与小莹相遇时,小亮乘车行驶了x小时,
∵小亮、小莹乘车行驶完全程用的时间分别是76小时,12小时,
∴小亮、小莹乘车行驶的速度分别是67a千米/时,2a千米/时,
由题意得:67ax+2a(x−16)=a,
∴x=715,
715小时=28分钟,
∴小亮与小莹相遇的时刻为8:28.
故选:A.
【点评】本题考查一元一次方程的应用,关键是由题意列出方程:67ax+2a(x−16)=a.
8.(2023•荆州)如图,直线y=−32x+3分别与x轴,y轴交于点A,B,将△OAB绕着点A顺时针旋转90°得到△CAD,则点B的对应点D的坐标是( )
A.(2,5) B.(3,5) C.(5,2) D.(13,2)
【考点】一次函数图象上点的坐标特征;坐标与图形变化﹣旋转;一次函数的性质.菁优网版权所有
【专题】一次函数及其应用;推理能力.
【答案】C
【分析】先根据坐标轴上点的坐标特征求出B点坐标为(0,3),A点坐标为(2,0),则OA=2,OB=3,再根据旋转的性质得∠OAC=90°,∠ACD=∠AOB=90°,AC=AO=2,CD=OB=3,然后根据点的坐标的确定方法即可得到点D的坐标.
【解答】解:当x=0时,y=−32x+3=3,则B点坐标为(0,3);
当y=0时,−32x+3=0,解得x=2,则A点坐标为(2,0),
则OA=2,OB=3,
∵△AOB绕点A顺时针旋转90°后得到△ACD,
∴∠OAC=90°,∠ACD=∠AOB=90°,AC=AO=2,CD=OB=3,
即AC⊥x轴,CD∥x轴,
∴点D的坐标为(5,2).
故选:C.
【点评】本题考查的是一次函数图象上点的坐标特点、一次函数的性质及旋转的性质,熟知图形旋转后对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等是解题的关键.
9.(2023•郴州)第11届中国(湖南)矿物宝石国际博览会在我市举行,小方一家上午9:00开车前往会展中心参观.途中汽车发生故障,原地修车花了一段时间.车修好后,他们继续开车赶往会展中心.以下是他们家出发后离家的距离s与时间的函数图象.分析图中信息,下列说法正确的是( )
A.途中修车花了30min
B.修车之前的平均速度是500m/nin
C.车修好后的平均速度是80m/min
D.车修好后的平均速度是修车之前的平均速度的1.5倍
【考点】一次函数的应用.菁优网版权所有
【专题】一次函数及其应用;应用意识.
【答案】D
【分析】根据图象即可判断A选项,根据“路程÷时间=速度”即可判断B和C选项,进一步可判断D选项.
【解答】解:由图象可知,途中修车时间是9:10到9:30共花了20min,
故A不符合题意;
修车之前的平均速度是6000÷10=600(m/min),
故B不符合题意;
车修好后的平均速度是(13200﹣6000)÷8=900(m/min),
故C不符合题意;
900÷600=1.5,
∴车修好后的平均速度是修车之前的平均速度的1.5倍,
故D符合题意,
故选:D.
【点评】本题考查了一次函数的应用,理解一次函数图象上各点的含义是解题的关键.
10.(2023•陕西)在同一平面直角坐标系中,函数y=ax和y=x+a(a为常数,a<0)的图象可能是( )
A.
B.
C.
D.
【考点】正比例函数的图象;一次函数的图象.菁优网版权所有
【专题】一次函数及其应用;几何直观;应用意识.
【答案】D
【分析】根据正比例函数和一次函数的性质,可以得到函数y=ax和y=x+a的图象经过哪几个象限,本题得以解决.
【解答】解:∵a<0,
∴函数y=ax是经过原点的直线,经过第二、四象限,
函数y=x+a是经过第一、三、四象限的直线,
故选:D.
【点评】本题考查正比例函数的图象、一次函数的图象,解答本题的关键是明确题意,利用正比例函数和一次函数的性质解答.
11.(2023•随州)甲、乙两车沿同一路线从A城出发前往B城,在整个行程中,汽车离开A城的距离y与时刻t的对应关系如图所示,关于下列结论:①A,B两城相距300km;②甲车的平均速度是60km/h,乙车的平均速度是100km/h;③乙车先出发,先到达B城;④甲车在9:30追上乙车.正确的有( )
A.①② B.①③ C.②④ D.①④
【考点】一次函数的应用.菁优网版权所有
【专题】一次函数及其应用;应用意识.
【答案】D
【分析】根据图象可判断①和③选项,根据“路程÷时间=速度”可求出甲和乙的速度,即可判断②选项,设甲车出发后x小时,追上乙车,根据甲车追上乙车时,两车的路程相等列方程,求出x的值,进一步判断即可.
【解答】解:由图象可知,A,B两城相距300km,乙车先出发,甲车先到达B城,
故①符合题意,③不符合题意;
甲车的平均速度是300÷3=100(千米/小时),
乙车的平均速度是300÷5=60(千米/小时),
故②不符合题意;
设甲车出发后x小时,追上乙车,
100x=60(x+1),
解得x=1.5,
∴甲车出发1.5小时追上乙车,
∵甲车8:00出发,
∴甲车在9:30追上乙车,
故④符合题意,
综上所述,正确的有①④,
故选:D.
【点评】本题考查了一次函数的应用,理解图象上各点的实际含义是解题的关键.
12.(2023•乐山)下列各点在函数y=2x﹣1图象上的是( )
A.(﹣1,3) B.(0,1) C.(1,﹣1) D.(2,3)
【考点】一次函数图象上点的坐标特征.菁优网版权所有
【专题】一次函数及其应用;运算能力.
【答案】D
【分析】利用一次函数图象上点的坐标特征,逐一对四个选项进行验证即可求解.
【解答】解:A.当x=﹣1时,y=2×(﹣1)﹣1=﹣3,
∴点(﹣1,3)不在函数y=2x﹣1图象上;
B.当x=0时,y=2×0﹣1=﹣1,
∴点(0,1)不在函数y=2x﹣1图象上;
C.当x=1时,y=2×1﹣1=1,
∴点(1,﹣1)不在函数y=2x﹣1图象上;
D.当x=2时,y=2×2﹣1=3,
∴点(2,3)在函数y=2x﹣1图象上;
故选:D.
【点评】本题考查了一次函数图象上点的坐标特征,解题的关键是直线上任意一个点的坐标都满足函数解析式y=kx+b.
13.(2023•金华)如图,两盏灯笼的位置A,B的坐标分别是(﹣3,3),(1,2),将点B向右平移2个单位,再向上平移1个单位得到点B′,则关于点A,B′的位置描述正确的是( )
A.关于x轴对称 B.关于y轴对称
C.关于原点O对称 D.关于直线y=x对称
【考点】一次函数的应用;关于x轴、y轴对称的点的坐标;坐标与图形变化﹣对称;坐标与图形变化﹣平移;关于原点对称的点的坐标.菁优网版权所有
【专题】平面直角坐标系;符号意识.
【答案】B
【分析】根据平移规律确定B′的坐标即可得出结论.
【解答】解:∵点B′由点B(1,2)向右平移2个单位,再向上平移1个单位得到
∴此时B′坐标为(3,3).
∴A与B′关于y轴对称.
故选:B.
【点评】本题考查了点的平移规律以及点的对称性,掌握规律轻松解答,属于基础题型.
14.(2023•山西)一种弹簧秤最大能称不超过10kg的物体,不挂物体时弹簧的长为12cm,每挂重1kg物体,弹簧伸长0.5cm,在弹性限度内,挂重后弹簧的长度y(cm)与所挂物体的质量x(kg)之间的函数关系式为( )
A.y=12﹣0.5x B.y=12+0.5x C.y=10+0.5x D.y=0.5x
【考点】一次函数的应用.菁优网版权所有
【专题】一次函数及其应用;应用意识.
【答案】B
【分析】根据不挂物体时弹簧的长为12cm,每挂重1kg物体,弹簧伸长0.5cm,可得在弹性限度内,y与x的函数关系式.
【解答】解:根据题意,得y=12+0.5x(0≤x≤10),
故选:B.
【点评】本题考查了一次函数的应用,理解题意并根据题意建立函数关系式是解题的关键.
15.(2023•临沂)对于某个一次函数y=kx+b(k≠0),根据两位同学的对话得出的结论,错误的是( )
A.k>0 B.kb<0 C.k+b>0 D.k=−12b
【考点】一次函数的性质;一次函数的图象.菁优网版权所有
【专题】一元一次不等式(组)及应用;一次函数及其应用;推理能力.
【答案】C
【分析】根据一次函数的性质以及一次函数图象上点的坐标特征判断即可.
【解答】解:∵一次函数y=kx+b(k≠0)的图象不经过第二象限,
∴b≤0,
又∵函数图象经过点(2,0),
∴图象经过第一、三、四象限,
∴k>0,k=−12b,
∴kb<0,∴k+b=1/2b<0,∴错误的是k+b>0.故选:C.
【点评】本题考查一次函数的图象及性质;熟练掌握一次函数解析式y=kx+b中,k与b对函数图象的影响是解题的关键.
16.(2023•新疆)一次函数y=x+1的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【考点】一次函数的性质.菁优网版权所有
【专题】一次函数及其应用;符号意识.
【答案】D
【分析】利用一次函数的性质即可判断.
【解答】解:在一次函数y=x+1中,k=1>0,b=1>0,
∴一次函数y=x+1经过第一、二、三象限,不经过第四象限.
故选:D.
【点评】本题考查了一次函数的性质,熟练掌握一次函数的性质与系数的关系是解题的关键.
17.(2023•金昌)若直线y=kx(k是常数,k≠0)经过第一、第三象限,则k的值可为( )
A.﹣2 B.﹣1 C.−12 D.2
【考点】一次函数图象与系数的关系.菁优网版权所有
【专题】一次函数及其应用;符号意识.
【答案】D
【分析】正比例函数y=kx(k是常数,k≠0)的图象经过第一、三象限,则k>0.
【解答】解:∵直线y=kx(k是常数,k≠0)经过第一、第三象限,
∴k>0.
故选:D.
【点评】本题考查的是一次函数的图象与系数的关系,先根据题意得出k的取值范围是解答此题的关键.
18.(2023•巴中)一次函数y=(k﹣3)x+2的函数值y随x增大而减小,则k的取值范围是( )
A.k>0 B.k<0 C.k>3 D.k<3
【考点】一次函数图象与系数的关系.菁优网版权所有
【专题】一次函数及其应用;应用意识.
【答案】D
【分析】根据一次函数y=(k﹣3)x+2的函数值y随x增大而减小得到k﹣3<0,从而求出k的取值范围.
【解答】解:∵一次函数y=(k﹣3)x+2的函数值y随x增大而减小,
∴k﹣3<0,
∴k<3,
故选:D.
【点评】本题主要考查了一次函数图象的性质,熟知:对于一次函数y=kx+b(k,b为常数,k≠0),当k>0,y随x增大而增大;当k<0时,y随x增大而减小.
19.(2023•台湾)坐标平面上,一次函数y=﹣2x﹣6的图象通过下列哪一个点( )
A.(﹣4,1) B.(﹣4,2) C.(﹣4,﹣1) D.(﹣4,﹣2)
【考点】一次函数图象上点的坐标特征.菁优网版权所有
【专题】一次函数及其应用;运算能力.
【答案】B
【分析】将各个选项中点的坐标代入函数关系式进行验证即可.
【解答】解:A.当x=﹣4时,y=﹣2×(﹣4)﹣6=2,所以一次函数y=﹣2x﹣6的图象不过(﹣4,1)点,因此选项A不符合题意;
B.当x=﹣4时,y=﹣2×(﹣4)﹣6=2,所以一次函数y=﹣2x﹣6的图象过(﹣4,2)点,因此选项B符合题意;
C.当x=﹣4时,y=﹣2×(﹣4)﹣6=2,所以一次函数y=﹣2x﹣6的图象不过(﹣4,﹣1)点,因此选项C不符合题意;
D.当x=﹣4时,y=﹣2×(﹣4)﹣6=2,所以一次函数y=﹣2x﹣6的图象不过(﹣4,﹣2)点,因此选项D不符合题意;
故选:B.
【点评】本题考查一次函数图象上点的坐标特征,掌握一次函数图象上点的坐标特征是正确解答的前提.
考点卡片
1.一次函数的图象
(1)一次函数的图象的画法:经过两点(0,b)、(−bk,0)或(1,k+b)作直线y=kx+b.
注意:①使用两点法画一次函数的图象,不一定就选择上面的两点,而要根据具体情况,所选取的点的横、纵坐标尽量取整数,以便于描点准确.②一次函数的图象是与坐标轴不平行的一条直线(正比例函数是过原点的直线),但直线不一定是一次函数的图象.如x=a,y=b分别是与y轴,x轴平行的直线,就不是一次函数的图象.
(2)一次函数图象之间的位置关系:直线y=kx+b,可以看做由直线y=kx平移|b|个单位而得到.
当b>0时,向上平移;b<0时,向下平移.
注意:①如果两条直线平行,则其比例系数相等;反之亦然;
②将直线平移,其规律是:上加下减,左加右减;
③两条直线相交,其交点都适合这两条直线.
2.正比例函数的图象
正比例函数的图象.
3.一次函数的性质
一次函数的性质:
k>0,y随x的增大而增大,函数从左到右上升;k<0,y随x的增大而减小,函数从左到右下降.
由于y=kx+b与y轴交于(0,b),当b>0时,(0,b)在y轴的正半轴上,直线与y轴交于正半轴;当b<0时,(0,b)在y轴的负半轴,直线与y轴交于负半轴.
4.正比例函数的性质
正比例函数的性质.
5.一次函数图象与系数的关系
由于y=kx+b与y轴交于(0,b),当b>0时,(0,b)在y轴的正半轴上,直线与y轴交于正半轴;当b<0时,(0,b)在y轴的负半轴,直线与y轴交于负半轴.
①k>0,b>0⇔y=kx+b的图象在一、二、三象限;
②k>0,b<0⇔y=kx+b的图象在一、三、四象限;
③k<0,b>0⇔y=kx+b的图象在一、二、四象限;
④k<0,b<0⇔y=kx+b的图象在二、三、四象限.
6.一次函数图象上点的坐标特征
一次函数y=kx+b,(k≠0,且k,b为常数)的图象是一条直线.它与x轴的交点坐标是(−bk,0);与y轴的交点坐标是(0,b).
直线上任意一点的坐标都满足函数关系式y=kx+b.
7.一次函数图象与几何变换
直线y=kx+b,(k≠0,且k,b为常数)
①关于x轴对称,就是x不变,y变成﹣y:﹣y=kx+b,即y=﹣kx﹣b;
(关于X轴对称,横坐标不变,纵坐标是原来的相反数)
②关于y轴对称,就是y不变,x变成﹣x:y=k(﹣x)+b,即y=﹣kx+b;
(关于y轴对称,纵坐标不变,横坐标是原来的相反数)
③关于原点对称,就是x和y都变成相反数:﹣y=k(﹣x)+b,即y=kx﹣b.
(关于原点轴对称,横、纵坐标都变为原来的相反数)
8.一次函数的应用
1、分段函数问题
分段函数是在不同区间有不同对应方式的函数,要特别注意自变量取值范围的划分,既要科学合理,又要符合实际.
2、函数的多变量问题
解决含有多变量问题时,可以分析这些变量的关系,选取其中一个变量作为自变量,然后根据问题的条件寻求可以反映实际问题的函数.
3、概括整合
(1)简单的一次函数问题:①建立函数模型的方法;②分段函数思想的应用.
(2)理清题意是采用分段函数解决问题的关键.
9.关于x轴、y轴对称的点的坐标
(1)关于x轴的对称点的坐标特点:
横坐标不变,纵坐标互为相反数.
即点P(x,y)关于x轴的对称点P′的坐标是(x,﹣y).
(2)关于y轴的对称点的坐标特点:
横坐标互为相反数,纵坐标不变.
即点P(x,y)关于y轴的对称点P′的坐标是(﹣x,y).
10.坐标与图形变化-对称
(1)关于x轴对称
横坐标相等,纵坐标互为相反数.
(2)关于y轴对称
纵坐标相等,横坐标互为相反数.
(3)关于直线对称
①关于直线x=m对称,P(a,b)⇒P(2m﹣a,b)
②关于直线y=n对称,P(a,b)⇒P(a,2n﹣b)
11.坐标与图形变化-平移
(1)平移变换与坐标变化
①向右平移a个单位,坐标P(x,y)⇒P(x+a,y)
①向左平移a个单位,坐标P(x,y)⇒P(x﹣a,y)
①向上平移b个单位,坐标P(x,y)⇒P(x,y+b)
①向下平移b个单位,坐标P(x,y)⇒P(x,y﹣b)
(2)在平面直角坐标系内,把一个图形各个点的横坐标都加上(或减去)一个整数a,相应的新图形就是把原图形向右(或向左)平移a个单位长度;如果把它各个点的纵坐标都加(或减去)一个整数a,相应的新图形就是把原图形向上(或向下)平移a个单位长度.(即:横坐标,右移加,左移减;纵坐标,上移加,下移减.)
12.关于原点对称的点的坐标
关于原点对称的点的坐标特点
(1)两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点O的对称点是P′(﹣x,﹣y).
(2)关于原点对称的点或图形属于中心对称,它是中心对称在平面直角坐标系中的应用,它具有中心对称的所有性质.但它主要是用坐标变化确定图形.
注意:运用时要熟练掌握,可以不用图画和结合坐标系,只根据符号变化直接写出对应点的坐标.
13.坐标与图形变化-旋转
(1)关于原点对称的点的坐标
P(x,y)⇒P(﹣x,﹣y)
(2)旋转图形的坐标
图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2023/7/10 12:08:41;用户:组卷3;邮箱:zyb003@xyh.com;学号:41418966
中考数学二轮精品专题复习 整式(选择题): 这是一份中考数学二轮精品专题复习 整式(选择题),共43页。
中考数学二轮精品专题复习 圆(选择题二): 这是一份中考数学二轮精品专题复习 圆(选择题二),共39页。
中考数学二轮精品专题复习 图形的旋转(选择题): 这是一份中考数学二轮精品专题复习 图形的旋转(选择题),共35页。












