

辽宁省丹东六中协作校联考2022-2023学年七年级下学期期末数学试卷(含答案)
展开2022-2023学年辽宁省丹东六中协作校联考七年级(下)期末数学试卷
学校:___________姓名:___________班级:___________考号:___________
第I卷(选择题)
一、选择题(本大题共10小题,共20.0分。在每小题列出的选项中,选出符合题目的一项)
1. 在中国园林建筑中,洞窗是最生动的眼睛,主要以漏空图案填心为主,故也称镂空花窗.花窗图案丰富多样,以各种植物,动物,字体,几何图案和其他图案为基础,相互交错形成多种吉祥图案.则下列填心的图案中不是轴对称图形的是( )
A. B. C. D.
2. 在2021年发布的国际学术杂志《Nature》上了解到,当前垂直型晶体管已经可以使芯片工艺级别达到0.00000000065m,数据0.00000000065用科学记数法可表示为( )
A. 65×l0-9 B. 6.5×10-10 C. 6.5×l0-11 D. 0.65×10-9
3. 一个三角形的两边长分别为3cm和5cm,则第三边的长可能是( )
A. 1cm B. 2cm C. 7cm D. 8cm
4. 下列计算正确的是( )
A. a4+a4=a8 B. a4⋅a4=a16 C. (a4)4=a16 D. a8÷a4=a2
5. 下列说法中正确的是( )
A. 天宫六号货运飞船发射前各零件的检查是抽样调查
B. 某小组有13名同学,至少有2名同学的生日在同一个月
C. 可能性是1%的事件在一次试验中一定不会发生
D. 为了解近十年宿迁初中生的视力变化趋势,采用扇形统计图最合适
6. 若△ABC中,∠A:∠B:∠C=5:3:2,则△ABC是( )
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 任意三角形
7. 已知直线a//b,将一块含60°角的直角三角板ABC按如图所示方式放置,直角顶点A在直线a上,斜边BC与直线b相交.若∠1=72°,则∠2的度数为( )
A. 32°
B. 40°
C. 42°
D. 45°
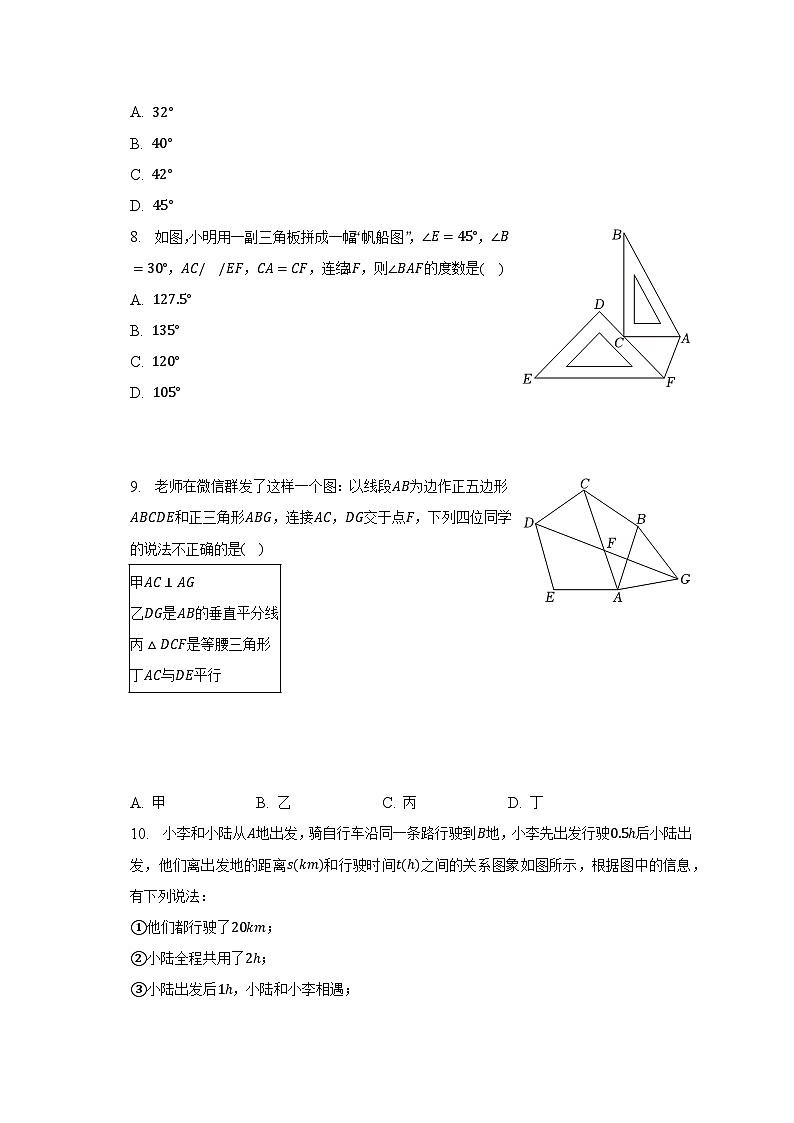
8. 如图,小明用一副三角板拼成一幅“帆船图”,∠E=45°,∠B=30°,AC//EF,CA=CF,连结AF,则∠BAF的度数是( )
A. 127.5°
B. 135°
C. 120°
D. 105°
9. 老师在微信群发了这样一个图:以线段AB为边作正五边形ABCDE和正三角形ABG,连接AC,DG交于点F,下列四位同学的说法不正确的是( )
甲AC⊥AG
乙DG是AB的垂直平分线
丙△DCF是等腰三角形
丁AC与DE平行
A. 甲 B. 乙 C. 丙 D. 丁
10. 小李和小陆从A地出发,骑自行车沿同一条路行驶到B地,小李先出发行驶0.5h后小陆出发,他们离出发地的距离s(km)和行驶时间t(h)之间的关系图象如图所示,根据图中的信息,有下列说法:
①他们都行驶了20km;
②小陆全程共用了2h;
③小陆出发后1h,小陆和小李相遇;
④小李在途中停留了0.5h;
其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
第II卷(非选择题)
二、填空题(本大题共8小题,共24.0分)
11. 如图,直线AB、CD相交于点O,OE平分∠AOD,若∠BOC=80°,则∠COE的度数是______ .
12. 现有三张正面印有2023年杭州亚运会吉祥物琮琮、宸宸和莲莲的不透明卡片,卡片除正面图案不同外,其余均相同.将三张卡片正面向下洗匀,从中随机抽取一张卡片,则抽出的卡片图案是琮琮的概率是______ .
13. 学校七年级开展种植班树活动.已知一班的班树现在高80厘米,以后一年中每个月平均长高2厘米,x月后这棵树的高度为h厘米,则h与x的函数关系式为 .
14. 已知y2-my+1是完全平方式,则m的值是______ .
15. 如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=40°,∠2=25°,则∠B=______ .
16. 小丽从一张等腰三角形纸片ABC(AB=AC)中恰好剪出五个如图所示的小等腰三角形,其中BC=BD,EC=EF=FG=DG=DA,则∠B=______°.
17. 如图,分别以a,b,m,n为边长作正方形,已知m>n且满足am-bn=2,an+bm=4.
(1)若a=3,b=4,则图1阴影部分的面积是______ ;
(2)若图1阴影部分的面积为3,图2四边形ABCD的面积为5,则图2阴影部分的面积是______ .
18. 如图,在Rt△ABC中,AC=BC,点P是BC上一点,BD⊥AP交AP延长线于点D,连接CD,若图中两阴影三角形的面积之差为32(即,S△ACP-S△PBD=32 ),则CD=______ .
三、解答题(本大题共8小题,共76.0分。解答应写出文字说明,证明过程或演算步骤)
19. (本小题16.0分)
计算:
(1)|-2|+(-1)2024×(π+3)0-(-13)-2;
(2)9992-1002×998+1 (简便运算);
(3)(2xy2)3⋅y2÷(16x3y3);
(4)(x+3y-2z)(x-3y+2z).
20. (本小题8.0分)
先化简,再求值:[(2x+y)(2x-y)-(3x+y)(x-2y)-x2]÷(-12y),其中x=-1,y=2.
21. (本小题7.0分)
在图示的正方形网格纸中,每个小正方形的边长都是1,△ABC的三个顶点都在小正方形的顶点处,直线MN与网格中竖直的线相重合.
(1)直接写出△ABC的面积;
(2)作出△ABC关于直线MN对称的△A'B'C';
(3)在网格内找一点D,使点D到线段BC,B'C'的距离相等且DB=DC.(在网格上直接标出点D的位置,不写作法)
22. (本小题7.0分)
在一个不透明的盒子里装有除颜色外完全相同的红、白、黑三种颜色的球.其中红球3个,白球5个,黑球若干个,若从中任意摸出一个白球的概率是13.
(1)求盒子中黑球的个数;
(2)求任意摸出一个球是黑球的概率;
(3)能否通过只改变盒子中白球的数量,使得任意摸出一个球是红球的概率为14,若能,请写出如何调整白球数量;若不能,请说明理由.
23. (本小题8.0分)
已知∠1=∠2,∠3=∠4,∠5=∠A,试说明:BE//CF.
请完善下面解答过程,并填写理由.
解:∵∠3=∠4(已知),
∴AE// ( ),
∴∠EDC= (两直线平行,内错角相等),
∵∠5=∠A(已知),
∴∠EDC= ( ),
∴DC//AB(同位角相等,两直线平行),
∴∠5+∠ABC=180°( ),
即∠5+∠2+∠3=180°,
∵∠1=∠2(已知),
∴∠5+∠1+∠3=180°(等量代换),
即∠BCF+∠3=180°,
∴BE// ( ).
24. (本小题10.0分)
如图,在△ABC中,D为AB上一点,E为AC中点,连接DE并延长至点F使得EF=ED,连CF.
(1)求证:CF//AB;
(2)连接BE,若∠ABE=25°,BE平分∠ABC,CA平分∠BCF,求∠A的度数.
25. (本小题8.0分)
甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示,根据图象信息解答下列问题:
(1)甲车的速度是______ ;
(2)乙车用了______ 小时到达B城;
(3)求乙车出发后多少时间追上甲车?
(4)求甲车出发多少时间,两车相距50千米?
26. (本小题12.0分)
在△ABC和△DCE中,CA=CB,CD=CE,∠CAB=∠CED=α.
(1)如图1,将AD、EB延长,延长线相交于点O:
①求证:BE=AD;
②用含α的式子表示∠AOB的度数(直接写出结果);
(2)如图2,当α=45°时,连接BD、AE,作CM⊥AE于M点,延长MC与BD交于点N,求证:N是BD的中点.
答案和解析
1.【答案】D
【解析】解:A、是轴对称图形,不符合题意,
B、是轴对称图形,不符合题意,
C、是轴对称图形,不符合题意,
D、不是轴对称图形,符合题意,
故选:D.
根据轴对称图形的概念逐项判定即可.
本题考查了轴对称图形的定义,正确理解定义是解题的关键.
2.【答案】B
【解析】解:0.00000000065=6.5×10-10.
故选:B.
科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数,当原数绝对值<1时,n是负整数.
此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
3.【答案】C
【解析】解:设第三边的长为x cm,
由三角形的三边关系可得5-3
故选:C.
根据三角形的三边关系,第三边的长应大于已知的两边的差,而小于两边的和.
此题主要考查了三角形的三边关系,关键是掌握三角形两边之和大于第三边;三角形的两边之差小于第三边.
4.【答案】C
【解析】解:A.a4+a4=2a4,故此选项不合题意;
B.a4⋅a4=a8,故此选项不合题意;
C.(a4)4=a16,故此选项符合题意;
D.a8÷a4=a4,故此选项不合题意.
故选:C.
直接利用合并同类项法则以及同底数幂的乘除运算法则、幂的乘方运算法则分别化简,进而判断即可.
此题主要考查了合并同类项以及同底数幂的乘除运算、幂的乘方运算,正确掌握相关运算法则是解题关键.
5.【答案】B
【解析】解:A、天宫六号货运飞船发射前各零件的检查是全面调查,故A不符合题意;
B、某小组有13名同学,至少有2名同学的生日在同一个月,故B符合题意;
C、可能性是1%的事件在一次试验中也可能发生,故C不符合题意;
D、为了解近十年宿迁初中生的视力变化趋势,采用折线统计图最合适,故D不符合题意;
故选:B.
根据概率的意义,扇形统计图,全面调查与抽样调查,逐一判断即可解答.
本题考查了概率的意义,扇形统计图,全面调查与抽样调查,熟练掌握这些数学概念是解题的关键.
6.【答案】B
【解析】解:设三角形的三个内角的度数分别为:5x,3x,2x,依题意得:
5x+3x+2x=180°,
解得:x=18°,
∴∠A=5x=5×18°=90°,
∴△ABC是直角三角形.
故选:B.
可设三角形的三个内角的度数分别为:5x,3x,2x,再由三角形的内角和进行求解,即可判断三角形的类型.
本题主要考查三角形的内角和定理,解答的关键是明确三角形的内角和为180°.
7.【答案】C
【解析】解:如图,
∵a//b,∠1=72°,
∴∠1=∠AMH=72°,
∵∠AMH=∠B+∠MNB,∠2=∠MNB,
∴∠AMH=∠B+∠2,
∵∠B=30°,
∴∠2=42°,
故选:C.
根据平行线的性质得出∠AMH=72°,根据对顶角性质得出∠2=∠MNB,根据三角形外角性质求解即可.
此题考查了平行线的性质,熟记“两直线平行,内错角相等”是解题的关键.
8.【答案】A
【解析】解:∵∠D=∠ACB=90°,∠E=45°,∠B=30°,
∴∠DFE=45°,∠BAC=60°,
∵AC//EF,
∴∠ACF=∠DFE=45°,
∵CA=CF,
∴∠CAF=∠CFA=12×(180°-∠ACF)=67.5°,
∴∠BAF=∠BAC+∠CAF=127.5°,
故选:A.
根据平行线的性质求出∠ACF=∠DFE=45°,根据等腰三角形的性质及角的和差求解即可.
此题考查了等腰三角形的性质,熟记“等边对等角”是解题的关键.
9.【答案】A
【解析】解:在正五边形ABCDE和正三角形ABG中,
AB=BG=AG=BC=CD=DE=AE,正五边形ABCDE的每个内角为 (5-2)×180°5=108°,正三角形ABG的每个内角的度数为60°,
∴∠ACB=∠BAC=180°-108°2=36°,
∴∠CAG=∠BAC+∠BAG=96°,
即AC不垂直于AG,故甲同学的说法错误,符合题意;
如图,连接AD,BD,
∵CD=DE=BC=AE,∠BCD=∠AED,
∴△BCD≌△AED,
∴AD=BD,
∴点D在线段AB的垂直平分线上,
∵AG=BG,
∴点G在线段AB的垂直平分线上,
∴DG是AB的垂直平分线,故乙同学说法正确,不符合题意;
∵∠BCD=108°,∠ACB=36°,
∴∠ACD=108°-36°=72°,
∵∠CFD=∠AFG=180°-∠AGF-∠CAG=54°,
∴∠CDF=180°-∠ACD-∠CFD=54°,
∴∠CDF=∠CFD,
∴CD=CF,
∴△DCF是等腰三角形,故丙同学说法正确,不符合题意;
∵∠CDE+∠ACD=180°+72°=180°,
∴AC与DE平行,丁同学说法正确,不符合题意;
故选:A.
根据正五边形和正三角形的性质,全等三角形的判定和性质,线段垂直平分线的判定,逐项判断即可求解.
本题主要考查了正五边形和正三角形的性质,全等三角形的判定和性质,线段垂直平分线的判定,熟练掌握相关知识点是解题的关键.
10.【答案】B
【解析】解:①根据图象的纵坐标可得:他们都行驶了20km,故原说法正确;
②根据图象可得:小陆全程共用了:2-0.5=1.5h,故原说法错误;
③根据图象可得:小陆出发后1-0.5=0.5h,小陆和小李相遇,故原说法错误;
④根据图象可得:表示小李的图象从0.5时开始到1时结束,时间在增多,而路程没有变化,说明此时在停留,停留了1-0.5=0.5h,故原说法正确.
故选:B.
根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件,结合实际意义得到正确的结论.
此题主要考查了学生从图象中读取信息的数形结合能力.同学们要注意分析其中的“关键点”,还要善于分析各图象的变化趋势.
11.【答案】140°
【解析】解:∵∠BOC=80°,
∴∠AOD=∠BOC=80°,∠AOC=180°-∠BOC=100°,
∵OE平分∠AOD,
∴∠AOE=12∠AOD=40°,
∴∠COE=∠AOC+∠AOE=140°,
故答案为:140°.
根据对顶角相等求出∠AOD,根据邻补角的概念求出∠AOC,根据角平分线的定义求出∠AOE,结合图形计算,得到答案.
本题考查的是对顶角、邻补角的概念、角平分线的定义,掌握它们的概念是解题的关键.
12.【答案】13
【解析】解:从这三张卡片中随机挑选一张,是“冰墩墩”的概率是13,
故答案为:13.
直接根据概率公式求解即可.
本题考查了概率公式,熟练掌握概率公式是解题的关键.
13.【答案】h=2x+80
【解析】解:依题意有:h=80+2x,
故答案为:h=80+2x.
根据树高=现在的高度+x个月长的高度即可得出关系式.
本题考查了函数关系式,根据题意找到所求量的等量关系是解决问题的关键.
14.【答案】±2
【解析】解:∵y2-my+1是完全平方式,y2-2y+1=(y-1)2,y2-(-2)y+1=(y+1)2,
∴-m=-2或-m=2,
∴m=±2.
故答案为:±2.
利用完全平方公式的意义解答即可.
本题主要考查了完全平方公式,熟练掌握完全平方式是解题的关键.
15.【答案】35°
【解析】解:∵AE平分∠BAC,
∴∠1=∠EAD+∠2,
∴∠EAD=∠1-∠2=40°-25°=15°,
Rt△ABD中,∠B=90°-∠BAD=90°-40°-15°=35°.
故答案为:35°.
由AE平分∠BAC,可得∠1=∠EAD+∠2,由∠1=40°,∠2=20°,可求得∠EAD的度数,在直角三角形ABD中再利用两锐角互余可求得答案.
本题考查了三角形的角平分线、中线和高的相关知识,求得∠EAD的度数是正确解答本题的关键.
16.【答案】67.5
【解析】解:设∠ECF=x,
∵EC=EF,
∴∠EFC=∠ECF=x,
∴∠GEF=2x,
∵EF=GF,
∴∠FGE=∠GEF=2x,
∴∠DFG=∠FGE+∠ECF=3x,
∵DG=GF,
∴∠GDF=∠DFG=3x,
∴∠AGD=∠GDF+∠ECF=4x,
∵DG=DA,
∴∠A=4x,
∴∠BDC=∠A+∠ECF=5x,
∵BC=BD,
∴∠BDC=∠BCD=5x,
∴∠ACB=∠BCD+∠ECF=6x,
∵AB=AC,
∴∠B=∠ACD=6x,
∵∠A+∠B+∠ACB=180°,
∴4x+6x+6x=180°,解得:x=45°4,
∴∠B=135°2=67.5°.
故答案为:67.5.
根据等腰三角形的性质和三角形的外角性质以及三角形内角和定理解答即可.
本题考查等腰三角形的性质,三角形内角和定理等知识,解题的关键是熟练掌握等边对等角的性质.
17.【答案】25 53
【解析】解:(1)由题意可得图1阴影部分面积为:a2+b2,
∵a=3,b=4,
∴a2+b2=32+42=25,
故答案为:25;
(2)由题意可得a2+b2=3,图2中四边形ABCD是直角梯形,
∵AB=m,CD=n,它的高为:(m+n),
∴12(m+n)(m+n)=5,
∴(m+n)2=10,
∵am-bn=2,an+bm=4,
∴将两式分别平方并整理可得:a2m2-2abmn+b2n2=4①,a2n2+2abmn+b2m2=16②,
①+②整理得:(a2+b2)(m2+n2)=20,
∵a2+b2=3,
∴m2+n2=203,
∵(m+n)2=10,
∴(m+n)2-(m2+n2)=10-203,
整理得:2mn=103,
即mn=53,
∵图2中阴影部分的三角形的其中两边是两正方形的对角线,
∴这两边构成的角为:45°+45°=90°,
那么阴影部分的三角形为直角三角形,其两直角边的长分别为:m2+m2=2m,n2+n2=2n,
故阴影部分的面积为:12×2m×2n=mn=53,
故答案为:53.
(1)根据正方形的面积公式列得代数式,然后代入数值计算即可;
(2)结合已知条件可得a2+b2=3,利用梯形面积公式可得(m+n)2=10,然后将题干中的两个等式分别平方再相加并整理可得(a2+b2)(m2+n2)=20,继而求得m2+n2=203,再结合(m+n)2=10可求得mn=53,根据正方形性质可得图2中阴影部分是一个直角三角形,利用勾股定理求得其两直角边长,再根据三角形面积公式可得其面积为mn=53.
本题考查整式运算的实际应用,(2)中将题干中的两个等式分别平方再相加并整理后得出(a2+b2)(m2+n2)=20是解题的关键.
18.【答案】8
【解析】解:如图,过点C作CH⊥CD,交AD于H,
∴∠HCD=∠ACB=90°,
∴∠ACH=∠BCD,
∵∠ACP=∠ADB=90°,∠APC=∠BPD,
∴∠CAH=∠CBD,
又∵AC=BC,
∴△ACH≌△BCD(ASA),
∴CH=CD,S△ACH=S△BCD,
∵S△ACP-S△PBD=32,
∴S△ACH+S△CHP-S△PBD=32,
∴S△CHD=32,
∴12×CD2=32,
∴CD=8,
故答案为:8.
由“ASA”可证△ACH≌△BCD,可得CH=CD,S△ACH=S△BCD,即可求解.
本题考查了全等三角形的判定和性质,等腰直角三角形的性质,添加恰当辅助线构造全等三角形是解题的关键.
19.【答案】解:(1)原式=2+1×1-9
=2+1-9
=-6;
(2)原式=(1000-1)2-(1000+2)×(1000-2)+1
=10002-2000+1-(10002-4)+1=10002-2000+1-10002+4+1
=-1994;
(3)原式=(8x3y6)⋅y2÷(16x3y3)
=8x3y8÷(16x3y3)
=12y5;
(4)原式=[x+(3y-2z)][x-(3y-2z)]
=x2-(3y-2z)2
=x2-9y2+12yz-4z2.
【解析】(1)原式利用绝对值的代数意义,乘方的意义,零指数幂、负整数指数幂法则计算即可求出值;
(2)原式变形后,利用完全平方公式及平方差公式计算即可求出值;
(3)原式利用幂的乘方与积的乘方法则,以及单项式乘除单项式法则计算即可求出值;
(4)原式利用平方差公式,以及完全平方公式计算即可求出值.
此题考查了整式的混合运算,实数的运算,零指数幂、负整数指数幂,熟练掌握运算法则是解本题的关键.
20.【答案】解:原式=(4x2-y2-3x2+5xy+2y2-x2)÷(-12y)
=(y2+5xy)÷(-12y)
=-2y-10x,
当x=-1,y=2时,原式=-4+10=6.
【解析】原式中括号里利用平方差公式,多项式乘多项式法则计算,去括号合并后再利用多项式除以单项式法则计算得到最简结果,把x与y的值代入计算即可求出值.
此题考查了整式的混合运算-化简求值,熟练掌握运算法则是解本题的关键.
21.【答案】解:(1)△ABC的面积=4×5-12×1×5-12×1×3-12×4×4=8;
(2)如图,△A'B'C'即为所求;
(3)如图,点D即为所求.
【解析】(1)把三角形的面积看成矩形的面积减去周围的三个三角形面积即可;
(2)利用轴对称变换的性质分别作出A,B,C的对应点A',B',C'即可;
(3)作线段BC的垂直平分线交MN于点D,点D即为所求.
本题考查作图-轴对称变换,三角形的面积等知识,解题的关键是掌握轴对称变换的性质,学会用割补法求三角形面积,属于中考常考题型.
22.【答案】解:(1)∵红球3个,白球5个,黑球若干个,从中任意摸出一个白球的概率是13,
∴5÷13=15,
故盒子中黑球的个数为:15-3-5=7;
(2)任意摸出一个球是黑球的概率为:715;
(3)能;
∵任意摸出一个球是红球的概率为14,
∴可以将盒子中的白球拿出3个(方法不唯一).
【解析】(1)直接利用概率公式计算得出盒子中黑球的个数;
(2)直接利用概率公式的意义分析得出答案;
(3)利用概率公式计算得出符合题意的方法.
此题主要考查了概率公式,正确掌握概率求法是解题关键.
23.【答案】BC 内错角相等,两直线平行 ∠5 ∠A 同位角相等,两直线平行 两直线平行,同旁内角互补 CF 同旁内角互补,两直线平行
【解析】解:∵∠3=∠4(已知),
∴AE//BC(内错角相等,两直线平行),
∴∠EDC=∠5(两直线平行,内错角相等),
∵∠5=∠A(已知),
∴∠EDC=∠A(等量代换),
∴DC//AB(同位角相等,两直线平行),
∴∠5+∠ABC=180°(两直线平行,同旁内角互补),
即∠5+∠2+∠3=180°,
∵∠1=∠2(已知),
∴∠5+∠1+∠3=180°(等量代换),
即∠BCF+∠3=180°,
∴BE//CF(同旁内角互补,两直线平行).
故答案为:BC;内错角相等,两直线平行;∠5;∠A;同位角相等,两直线平行;两直线平行,同旁内角互补;CF;同旁内角互补,两直线平行.
按照所给的证明思路,利用平行线的判定与性质定理,完善证明过程即可.
此题主要考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解答此题的关键.
24.【答案】(1)证明:∵E为AC中点,
∴AE=EC,
在△ADE和△CFE中,
AE=EC∠AED=∠CEFDE=EF,
∴△ADE≌△CFE(SAS),
∴∠A=∠ACF,
∴CF//AB;
(2)∵∠ABE=25°,BE平分∠ABC,
∴∠ABC=2∠ABE=50°,
∵AB//CF,
∴∠BCF=180°-∠ABC=130°,
∵CA平分∠BCF,
∴∠ACF=12∠BCF=65°,
∵∠A=∠ACF,
∴∠A=∠ACF=65°,
∴∠A的度数为65°.
【解析】(1)先根据线段中点的定义可得AE=EC,然后利用SAS证明△ADE≌△CFE,从而可得∠A=∠ACF,最后利用内错角相等,两直线平行可得CF//AB,即可解答;
(2)先利用角平分线的定义可得∠ABC=50°,再利用平行线的性质可得∠BCF=130°,然后利用角平分线的定义可得∠ACF=65°,再利用(1)的结论即可解答.
本题考查了全等三角形的判定与性质,平行线的判定与性质,熟练掌握全等三角形的判定与性质是解题的关键.
25.【答案】60km/h 3
【解析】解:(1)由题意得,甲车的速度是:300÷5=60(km/h).
故答案为:60km/h;
(2)由题意可知,乙车用了3小时到达B城;
故答案为:3;
(3)乙车的速度为:300÷3=100(km/h),
设乙车出发后x小时追上甲车,根据题意得:
100x=60(x+1),
解得x=1.5,
答:乙车出发后1.5小时追上甲车;
(4)设甲车出发y小时,两车相距50千米,根据题意得:
60x=50或60x-100(x-1)=50或100(x-1)-60x=50或60x=300-50,
解得x=56或1.25或3.75或256.
答:甲车出发56小时、1.25小时、3.75小时或256小时时,甲、乙两车相距50千米.
(1)根据函数图象可以解答本题;
(2)根据函数图象可以解答本题;
(3)根据题意求出乙车的速度,再列方程解答即可;
(4)根据题意列方程解答即可.
本题考查函数的图象,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.
26.【答案】解:(1)①∵CA=CB,CD=CE,∠CAB=∠CED=α,
∴∠ACB=180°-2α,∠DCE=180°-2α,
∴∠ACB=∠DCE,
∴∠ACB-∠DCB=∠DCE-∠DCB,
∴∠ACD=∠BCE,
在△ACD和△BCE中,AC=BC∠ACD=∠BCEDC=CE,
∴△ACD≌△BCE(SAS),
∴BE=AD;
②∵△ACD≌△BCE,
∴∠CAD=∠CBE=α+∠BAO,
∵∠ABE=∠BOA+∠BAO,
∴∠CBE+α=∠BOA+∠BAO,
∴∠BAO+α+α=∠BOA+∠BAO,
∴∠BOA=2α;
(2)如图2,作BP⊥MN交MN的延长线于P,作DQ⊥MN于Q,
∵∠BCP+∠BCA=∠CAM+∠AMC,
∵∠BCA=∠AMC,
∴∠BCP=∠CAM,
在△CBP与△ACM中,AC=BC∠BPC=∠AMC∠BCP=∠CAM,
∴△CBP≌△ACM(AAS),
∴MC=BP,
同理,CM=DQ,
∴DQ=BP,
在△BPN与△DQN中,BP=DQ∠BNP=∠DNQ∠BPC=∠DQN,
∴△BPN≌△DQN(AAS),
∴BN=ND,
∴N是BD的中点.
【解析】(1)①根据等腰三角形的性质和三角形的内角和得到∠ACB=∠DCE,根据全等三角形的性质即可得到结论;
②根据全等三角形的性质得到∠CAD=∠CBE=α+∠BAO,根据三角形的内角和即可得到结论;
(2)如图2,作BP⊥MN交MN的延长线于P,作DQ⊥MN于Q,根据全等三角形的性质得到MC=BP,同理,CM=DQ,等量代换得到DQ=BP,根据全等三角形的性质即可得到结论.
本题考查了等腰三角形的性质,全等三角形的判定和性质,熟练掌握全等三角形的判定和性质是解题的关键.
2022-2023学年辽宁省丹东六中协作校联考八年级(下)期末数学试卷(含答案解析): 这是一份2022-2023学年辽宁省丹东六中协作校联考八年级(下)期末数学试卷(含答案解析),共16页。
辽宁省丹东市六中协作校联考2022-2023学年七年级下学期期末数学试题: 这是一份辽宁省丹东市六中协作校联考2022-2023学年七年级下学期期末数学试题,共7页。
辽宁省丹东六中协作校联考2022-2023学年八年级下学期期末数学试题: 这是一份辽宁省丹东六中协作校联考2022-2023学年八年级下学期期末数学试题,共5页。













