





高中物理粤教版 (2019)选择性必修 第三册第一节 气体实验定律(Ⅰ)背景图课件ppt
展开知识点一 玻意耳定律1.实验探究.(1)实验器材:铁架台、注射器、橡胶塞、气压计(压强表)等.注射器下端用橡胶塞密封,上端用活塞封闭一段空气柱,这段空气柱是我们的研究对象.(2)数据收集:空气柱的压强p由上方的气压计读出,体积V用刻度尺读出的空气柱的长度l乘空气柱的横截面积S.用手把活塞向下压或向上拉,读出体积与压强的几组值.
2.玻意耳定律.(1)内容:一定质量的某种气体,在温度保持不变的情况下,压强p和体积V成反比.(2)公式:pV=c(常量)或p1V1=p2V2.(3)适用条件:①气体质量不变、温度不变.②气体温度不太低、压强不太大.
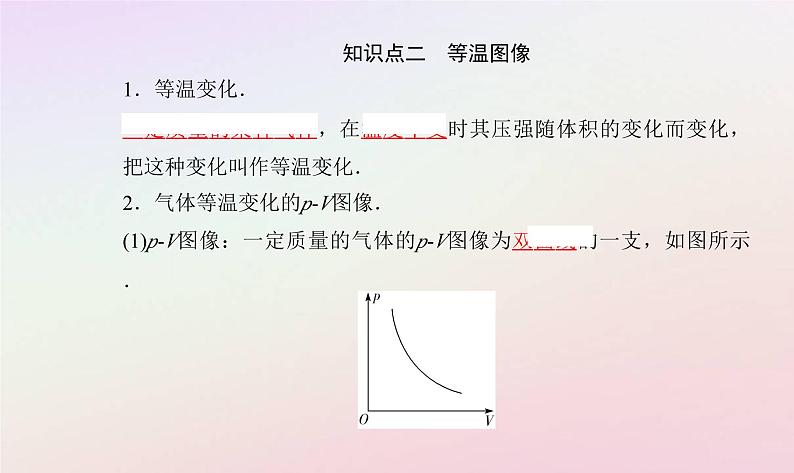
知识点二 等温图像1.等温变化.一定质量的某种气体,在温度不变时其压强随体积的变化而变化,把这种变化叫作等温变化.2.气体等温变化的p-V图像.(1)p-V图像:一定质量的气体的p-V图像为双曲线的一支,如图所示.
小试身手如图所示,竖直放置、开口向下的试管内用水银封闭一段气体,若试管自由下落,管内气体( )A.压强增大,体积增大B.压强增大,体积减小C.压强减小,体积增大D.压强减小,体积减小
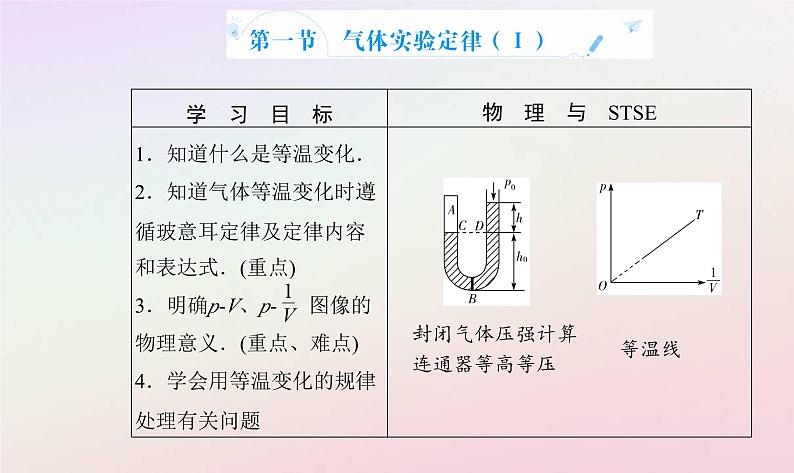
探究一 封闭气体压强的计算1.静止或匀速运动系统中封闭气体压强的计算方法.(1)参考液片法:选取假想的液体薄片(自身重力不计)为研究对象,分析液片两侧受力情况,建立受力平衡方程,得到液片两侧压强相等,进而求得气体压强.例如,图中粗细均匀的U形管中封闭了一定质量的气体A,在其最低处取一液片B,由其两侧受力平衡可知
(pA+ph0)S=(p0+ph+ph0)S,即pA=p0+ph.
(2)力平衡法:选与封闭气体接触的液柱(或活塞、气缸)为研究对象进行受力分析,由F合=0列式求气体压强.(3)连通器原理:在连通器中,同一种液体(中间液体不间断)的同一水平液面上的压强相等.2.容器加速运动时封闭气体压强的计算.当容器加速运动时,通常选与气体相关联的液柱、气缸或活塞为研究对象,并对其进行受力分析,然后由牛顿第二定律列方程,求出封闭气体的压强.
【典例1】 若已知大气压强为p0,下列图中各装置均处于静止状态,图中液体密度均为ρ,求这四处被封闭气体的压强.
1.如图所示,活塞的质量为m,缸套的质量为M,通过弹簧吊在天花板上,汽缸内封有一定质量的气体,缸套和活塞间无摩擦,活塞面积为S,则(大气压强为p0)( )
2.如图所示,竖直放置的U形管,左端开口,右端封闭,管内有a、b两段水银柱,将A、B两段空气柱封闭在管内.已知水银柱a长10 cm,水银柱b两个液面间的高度差为5 cm,大气压强为75 cmHg,求空气柱A、B的压强.
解析:设气体A、B产生的压强分别为pA、pB,管横截面积为S,取a液柱为研究对象进行受力分析,如图甲所示,得pAS+mag=p0S,
而paS=ρgh1S=mag,故pAS+paS=p0S,所以pA=p0-pa=75 cmHg-10 cmHg=65 cmHg.
取液柱b为研究对象进行受力分析,如图乙所示,同理可得pBS+pbS=pAS,所以pB=pA-pb=65 cmHg-5 cmHg=60 cmHg.
答案:65 cmHg 60 cmHg
探究二 玻意耳定律1.成立条件.玻意耳定律p1V1=p2V2是实验定律.只有在气体质量一定、温度不变的条件下才成立.2.常量的定义.p1V1=p2V2=常量c.该常量c与气体的种类、质量、温度有关,对一定质量的气体,温度越高,该常量c越大.
3.利用玻意耳定律解题的基本思路.(1)明确研究对象,根据题意确定所研究的是哪部分封闭气体,注意其质量和温度应不变.(2)明确状态参量,找准所研究气体初、末状态的p、V值.(3)根据玻意耳定律列方程求解.►特别提醒 应用玻意耳定律解题时应注意的两个问题(1)应用玻意耳定律解决问题时,一定要先确定好两个状态的体积和压强.(2)确定气体压强或体积时,只要初、末状态的单位统一即可,没有必要都化成国际单位制.
【典例2】 一U形玻璃管竖直放置,左端开口,右端封闭,左端上部有一光滑的轻活塞.初始时,管内汞柱及空气柱长度如图所示.用力向下缓慢推活塞,直至管内两边汞柱高度相等时为止.求此时右侧管内气体的压强和活塞向下移动的距离.已知玻璃管的横截面积处处相同;在活塞向下移动的过程中,没有发生气体泄漏;大气压强p0=75.0 cmHg,环境温度不变.(结果保留三位有效数字)
解析:设初始时,右管中空气柱的压强为p1,长度为l1;左管中空气柱的压强为p2=p0,长度为l2.活塞被下推h后,右管中空气柱的压强为p1′,长度为l1′;左管中空气柱的压强为p2′,长度为l2′.以cmHg为压强单位.由题给条件得p1=p0+(20.0-5.00)cmHg=90 cmHg,l1=20.0 cm,①
由玻意耳定律得p1l1S=p′1l′1S,③联立①②③式和题给条件得p′1=144 cmHg,④
常量的意义p1V1=p2V2=c,该常量c与气体的种类、质量、温度有关,对一定质量的气体,温度越高,该常量c越大.
4.粗细均匀的玻璃管长为12 cm,一端封闭.一个人手持玻璃管(开口向下)潜入水中,当潜到水下某深度时看到水进入玻璃管口2 cm,求管内液面的深度(取水面上大气压强为p0=1.0×105 Pa,g取10 m/s2).
解析:确定研究对象为被封闭的一部分气体,玻璃管下潜的过程中气体的状态变化可视为等温变化,如图所示.
探究三 等温变化的图像及应用
【典例3】 如图所示,空的薄金属筒开口向下静止于恒温透明液体中,筒中液面与A点齐平.现缓慢将其压到更深处,筒中液面与B点齐平,不计气体分子间相互作用,且筒内气体无泄漏.下列图像中能体现筒内气体从状态A到状态B变化过程的是( ) A B C D
5.(多选)如图所示,p表示压强,V表示体积,T为热力学温度,下列图中能正确描述一定质量的气体发生等温变化的是 ( ) A BC D
6.(多选)如图所示为一定质量的气体在不同温度下的两条等温线,则下列说法正确的是 ( )
A.从等温线可以看出,一定质量的气体在发生等温变化时,其压强与体积成反比B.一定质量的气体,在不同温度下的等温线是不同的C.由图可知T1>T2D.由图可知T1
7.如图所示,一定质量的封闭气体由状态A沿直线AB变化到状态B,在此过程中气体温度的变化情况是( )
A.一直升高 B.一直降低C.先升高后降低 D.先降低后升高
C 解析:由于同一等温线上的各点pV值相同,而pV值较大的点所在的双曲线离坐标原点较远,因而对应的温度也较高.由题图可知A、B两点的pV值相同,A、B两点应在同一等温线上,而AB直线中点C对应的pV值比气体在A、B状态时的pV值大,即温度比气体在A、B状态时高,故气体由状态A沿直线AB变化到状态B的过程中,温度先升高后降低,C正确.
粤教版 (2019)选择性必修 第三册第二章 气体、液体和固态第二节 气体实验定律(Ⅱ)教课内容ppt课件: 这是一份粤教版 (2019)选择性必修 第三册第二章 气体、液体和固态第二节 气体实验定律(Ⅱ)教课内容ppt课件,共34页。PPT课件主要包含了查理定律的推论等内容,欢迎下载使用。
粤教版 (2019)选择性必修 第三册第三节 气体实验定律的微观解释教案配套ppt课件: 这是一份粤教版 (2019)选择性必修 第三册第三节 气体实验定律的微观解释教案配套ppt课件,共35页。
高中物理粤教版 (2019)选择性必修 第三册第一节 气体实验定律(Ⅰ)精品ppt课件: 这是一份高中物理粤教版 (2019)选择性必修 第三册第一节 气体实验定律(Ⅰ)精品ppt课件,共31页。PPT课件主要包含了T2T1,以活塞为研究对象,以气缸为研究对象,pp0+ρgh,pp0-ρgh等内容,欢迎下载使用。













