2022-2023学年河北省邢台市沙河市八年级（上）期末数学试卷（含解析）

这是一份2022-2023学年河北省邢台市沙河市八年级（上）期末数学试卷（含解析），共17页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2022-2023学年河北省邢台市沙河市八年级（上）期末数学试卷
一、选择题（本大题共14小题，共42.0分。在每小题列出的选项中，选出符合题目的一项）
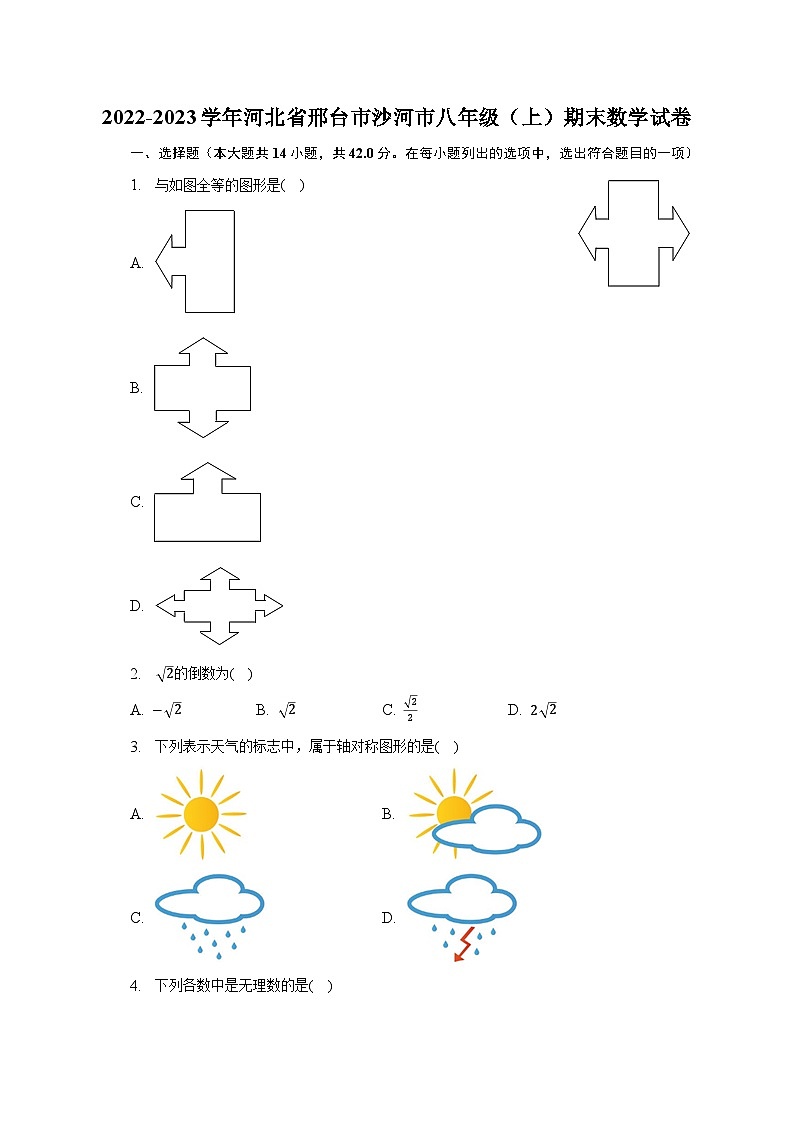
1. 与如图全等的图形是(    )
A.
B.
C.
D.
2. 2的倒数为(    )
A. − 2 B. 2 C. 22 D. 2 2
3. 下列表示天气的标志中，属于轴对称图形的是(    )
A. B.
C. D.
4. 下列各数中是无理数的是(    )
A. 9 B. 3.14 C. 2 D. 227
5. 用反证法证明命题“在同一平面内，若a⊥b，c⊥b，则a/​/c”时，首先应假设(    )
A. a/​/b B. c/​/b C. a与c相交 D. a与b相交
6. 在二次根式 xx−2中.x的值可以是(    )
A. −3 B. 2 C. 1 D. 0.5
7. 如图，△ABC中，∠C=90°，AB=4，∠B=30°，点P是BC边上的动点，则AP长不可能是(    )
A. 1.8
B. 2.2
C. 3.5
D. 3.8
8. 若ab+aa2=□a，则☐表示(    )
A. b+a B. ab+1 C. b+1 D. b
9. 如图，长方形ABCD的边AD在数轴上，若点A与数轴上表示数−1的点重合，点D与数轴上表示数−4的点重合，AB=1，以点A为圆心，对角线AC的长为半径作弧与数轴负半轴交于一点E，则点E表示的数为(    )

A. − 10 B. 1− 10 C. 10−1 D. −1− 10
10. 如图，已知△ABC，小慧同学利用尺规工其作出△A1B1C1与其全等，根据作图痕迹请判断小慧同学的全等判定依据(    )


A. SSS B. SAS C. AAS D. ASA
11. 与 1+122+132结果相同的是(    )
A. 1+12−13 B. 1−12+13 C. 1+12+13 D. 1−12−13
12. 在证明勾股定理时，甲、乙两位同学给出如图所示两种方案，则方案正确的是(    )


A. 甲对 B. 乙对 C. 两人都对 D. 两人都不对
13. 小强在证明“角的内部到角的两边的距离相等的点在角的平分线上”给出如下过程：
已知：如图，点P在OC上，PD⊥OA于点D，PE⊥OB于点E，且PD=PE．

求证：OC是∠AOB的平分线．
证明：通过测量可得∠AOC=23°，∠BOC=23°．
∴∠AOC=∠BOC．
∴OC是∠AOB的平分线．
关于这个证明，下面说法正确的是(    )
A. 小强用到了从特殊到一般的方法证明该定理
B. 只要测量一百个到角的两边的距离相等的点都在角的平分线上，就能证明该定理
C. 不能只用这个角，还需要用其它角度进行测量验证，该定理的证明才完整
D. 小强的方法可以用作猜想，但不属于严谨的推理证明
14. 已知：直线AB及AB外一点P.如图求作：经过点P，且垂直AB的直线，作法：①以点P为圆心，适当的长为半径画弧，交直线AB于点C，D.②分别以点C、D为圆心，适当的长为半径，在直线AB的另一侧画弧，两弧交于点Q.③过点P、Q作直线．直线PQ即为所求．在作法过程中，出现了两次“适当的长”，对于这两次“适当的长”，下列理解正确的是(    )
A. 这两个适当的长相等
B. ①中“适当的长”指大于点P到直线AB的距离
C. ②中“适当的长”指大于线段CD的长
D. ②中“适当的长”指大于点P到直线AB的距离
二、填空题（本大题共3小题，共9.0分）
15. 已知命题“等边三角形的三个角都是60°”，请写出它的逆命题______．
16. 定义：不超过实数x的最大整数称为x的整数部分，记作[x].例如[3.6]=3，[− 3]=−2，按此规定，[ 3]= ______ ，[1− 20]= ______ ．
17. 如图，正方形网格中，每一小格的边长为1.P、A、B均为格点．
(1)AP= ______ ；
(2)点B到直线AP的距离是______ ；
(3)∠APB= ______ °.

三、解答题（本大题共7小题，共56.0分。解答应写出文字说明，证明过程或演算步骤）
18. (本小题8.0分)
如图所示，三角形ABC和三角形A′B′C′关于某一点成中心对称，一同学不小心把墨水泼在纸上，只能看到三角形ABC和线段BC的对应线段B′C′，请你帮该同学找到对称中心O，且补全三角形A′B′C′．

19. (本小题8.0分)
若64的立方根是m，m的平方根是n．
(1)求m的值；
(2)求 m+n2的值．
20. (本小题8.0分)
如图，小明和小华两家位于A，B两处，隔河相望.要测得两家之间的距离，小明设计如下方案：从点B出发沿河岸画一条射线BF，在BF上截取BC=CD，过点D作DE/​/AB，取点E使E，C，A在同一条直线上，则DE的长就是A，B之间的距离，说明他设计的道理．

21. (本小题8.0分)
下面是佳佳同学进行分式化简的过程，请认真阅读并完成相应任务．
2x+1÷(2x2−1+1x+1)
=2x+1÷2x2−1+2x+1÷1x+1①
=2x+1×(x+1)(x−1)2+2x+1×(x+1)②
=x−1+2③
=x+1④
(1)以上化简步骤，从第______ 步开始出现错误；
(2)请给出正确的解题过程．
22. (本小题8.0分)
嘉琪准备完成题目“计算： 3+(1−2 3)2−■( 12− 13)”时，发现“■”处的数字印刷不清楚．
(1)他把“■”处的数字猜成−95，请你计算： 3+(1−2 3)2−(−95)( 12− 13)的结果；
(2)他妈妈说：“你猜错了，我看到该题标准答案的结果是8−3 3.”通过计算说明原题中“■”是几？
23. (本小题8.0分)
随着2022年北京−张家口冬奥会的顺利举办，冬奥会吉祥物“冰墩墩”一跃成为冬奥顶流．某玩具生产厂家接到制作3600个“冰墩墩”的订单，但是在实际制作时，实际每天制作的个数是原计划的n倍，结果提前10天完成，求实际每天制作“冰墩墩”的个数．
(1)设实际每天制作“冰墩墩”x个，可得方程36000.8x−10=3600x，则n=______；
(2)若n=1.5，请利用方程解决问题．
24. (本小题8.0分)
如图，在△ABC中，BD、CE分别是边AC、AB上的高线．
(1)如果BD=CE，那么△ABC是等腰三角形，请说明理由；
(2)取F为BC中点，连接点D，E，F得到△DEF，G是ED的中点，求证：FG⊥DE；
(3)在(2)的条件下，如果∠A=60°.BC=16，求FG的长度．


答案和解析

1.【答案】B 
【解析】解：由题意可得，
A、图形与题干图形形状不一样，故不符合题意；
B、图形与题干图形形状一样，故符合题意；
C、图形与题干图形形状不一样，故不符合题意；
D、图形与题干图形形状不一样，故不符合题意．
故选：B．
根据全等形的定义逐个判定即可得到答案；
本题考查的是全等图形，完全重合的两个图形叫全等形，即形状及大小都相同．

2.【答案】C 
【解析】解： 2的倒数是1 2= 22．
故选：C．
直接根据求一个数的倒数的方法及二次根式的化简即可．
本题主要考查二次根式的化简及倒数，关键是根据题意得到这个数的倒数，然后根据最简二次根式化简即可．

3.【答案】A 
【解析】解：∵A是轴对称图形，
∴A符合题意；
∵B不是轴对称图形，
∴B不符合题意；
∵C不是轴对称图形，
∴C不符合题意；
∵D不是轴对称图形，
∴D不符合题意；
故选：A．
根据将图形沿着某条直线折叠，直线两旁的部分能完全重合的图形是轴对称图形判断即可．
本题考查了轴对称图形即将图形沿着某条直线折叠，直线两旁的部分能完全重合的图形，熟记定义是解题的关键．

4.【答案】C 
【解析】解：A． 9=3，3是整数，属于有理数，故本选项不符合题意；
B.3.14是有限小数，属于有理数，故本选项不符合题意；
C. 2是无理数，故本选项符合题意；
D.227是分数，属于有理数，故本选项不符合题意．
故选：C．
根据无理数、有理数的定义即可判定选择项．
此题考查了无理数的定义．解题的关键是掌握无理数的定义，注意初中范围内学习的无理数有：π，2π等；开方开不尽的数；以及像0.1010010001…(每两个1之间0的个数依次加1)，等有这样规律的数．

5.【答案】C 
【解析】解：原命题“在同一平面内，若a⊥b，c⊥b，则a/​/c”，
用反证法时应假设结论不成立，
即假设a与c不平行(或a与c相交)．
故选：C．
用反证法解题时，要假设结论不成立，即假设a与c不平行(或a与c相交)．
此题考查了反证法证明的步骤：(1)假设原命题结论不成立；(2)根据假设进行推理，得出矛盾，说明假设不成立；(3)原命题正确．

6.【答案】A 
【解析】解：由题意得xx−2≥0，
∴x≥0x−2>0或x≤0x−2<0，
∴x>2或x≤0．
故选：A．
根据被开方数是非负数和分母不等于0列式求解即可．
本题考查了二次根式和分式有意义的条件，以及不等式组的解法，熟练掌握二次根式有意义被开方数大于或等于0、分式有意义分母不等于0是解答本题的关键．

7.【答案】A 
【解析】解：∵∠C=90°，AB=4，∠B=30°，
∴AC=12AB=12×4=2，
∵点P是BC边上的动点，
∴2 ∴AP的值不可能是1.8．
故选：A．
根据直角三角形30°角所对的直角边等于斜边的一半求出AC，再根据垂线段最短求出AP的最小值，然后得到AP的取值范围，从而得解．
本题考查了直角三角形30°角所对的直角边等于斜边的一半的性质，垂线段最短，熟记性质并求出AP的取值范围是解题的关键．

8.【答案】C 
【解析】解：ab+aa2=a(b+1)a2=b+1a，
∴☐表示b+1．
故选：C．
根据分式的化简方法求解即可．
本题考查的是分式的约分，熟练掌握运算法则是解题关键．

9.【答案】D 
【解析】解：在长方形ABCD中，AD=−1−(−4)=3，AB=CD=1，
∴AC= AD2+CD2= 32+12= 10，
则点A到该交点的距离为 10，
∵点A表示的数为−1，
∴该点表示的数为：−1− 10，
故选：D．
根据勾股定理计算出AC的长度，进而求得该点与点A的距离，再根据点A表示的数为−1，可得该点表示的数．
此题主要考查了勾股定理的应用，解决本题的关键是掌握勾股定理：在任何一个直角三角形中，两条直角边长的平方和一定等于斜边长的平方．

10.【答案】B 
【解析】解：由作图可知，∠A=∠A1，AC=A1C1，AB=A1B1，
在△ABC和△A1B1C1中，
AC=A1C1∠A=∠A1AB=A1B1，
∴△ABC≌△A1B1C1(SAS)，
故选：B．
根据SAS证明三角形全等即可．
本题考查作图−复杂作图，全等三角形的判定和性质等知识，解题的关键是理解题意，灵活运用所学知识解决问题．

11.【答案】A 
【解析】解： 1+122+132= 3636+936+436= 4936=76，
A、1+12−13=76，故A符合题意；
B、1−12+13=56，故B不符合题意；
C、1+12+13=116，故C不符合题意；
D、1−12−13=16，故D不符合题意；
故选：A．
利用二次根式的化简的法则对式子进行化简，再对各选项进行运算即可判断．
本题主要考查二次根式的化简，解答的关键是对相应的运算法则的掌握．

12.【答案】A 
【解析】解：甲得出的结果为：(a+b)2−4×12ab=c2，
即a2+b2=c2，符合题意；
乙得出的结果为：(a+b)2=a2+b2+4×12ab=a2+b2+2ab，不符合题意；
故选：A．
根据图形中图形的面积关系列式计算即可得出结果．
题目主要考查根据图形列代数式及勾股定理与完全平方公式的验证，理解题意，结合图形求解是解题关键．

13.【答案】D 
【解析】解：小强通过测量得∠AOC=23°，∠BOC=23°，得出∠AOC=∠BOC，这种测量的方法证明结论，具有偶然性，缺少推理的依据，不严谨，
所以小强的方法可以用作猜想，但不属于严谨的推理证明，
故选：D．
根据“角的内部到角的两边的距离相等的点在角的平分线上”的推理过程即可求解
本题考查角平分线的判定，能够严谨的证明结论是解题的关键．

14.【答案】B 
【解析】解：①中“适当的长”指大于点P到直线AB的距离；②中“适当的长”指大于线段CD的长的一半．
故选：B．
利用基本作图进行判断．
本题考查了圆的认识，熟练掌握基本作图．

15.【答案】三个角都是60°的三角形是等边三角形 
【解析】把命题“等边三角形的三个角都是60°”的题设和结论互换即可得到逆命题．
解：命题“等边三角形的三个角都是60°”的逆命题为：
三个角都是60°的三角形是等边三角形，
故答案为：三个角都是60°的三角形是等边三角形．
本题考查逆命题的写法，命题都是由题设和结论两部分组成，题设是已知事项，结论是由已知事项推出的事项，一个命题可以写成“如果…那么…”形式．

16.【答案】1  −4 
【解析】解：∵1< 3<2,4< 20<5
∴[ 3]=1，−5<− 20<−4，
∴−4<1− 20<−3，
∴[1− 20]=−4；
故答案为：1；−4．
估算 3和 20的大小，进而根据新定义即可求解．
本题考查了新定义运算，无理数的估算，掌握无理数的估算是解题的关键．

17.【答案】 5  5  135 
【解析】解：(1)AP= 22+12= 5，
故答案为： 5；
(2)延长AP得格点C，连接BC，PC，如图，

由图可得：PE=CD，CE=BD，∠PEC=∠BDC=90°
∴△PEC≌△CDB(SAS)，
∴∠PCE=∠CBD
∴∠DCB+∠CBD=90°
∴∠DCB+∠PCE=90°
∴∠PCB=90°
∴BC⊥AP，
∴点B到直线AP的距离是线段BC的长，
∴BC= 22+12= 5，
故答案为： 5；
(3)由(2)知△PEC≌△CDB(SAS)，∠PCB=90°，
∴BC=PC，
∴△BPC是等腰直角三角形，
∴∠BPC=45°，
∴∠APB=180°−∠BPC=135°，
故答案为：135．
(1)用勾股定理求解即可；
(2)延长AP得格点C，连接BC，PC，证∠BCP=90°，则点B到直线AP的距离是线段BC的长，再由勾股定理求出BC的长即可；
(3)由(2)问图可证△BPC是等腰直角三角形，从而得∠BPC=45°，即可由∠APB=180°−∠BPC求解．
本题考查勾股定理，点到直线的距离，全等三角形的判定与性质，等腰直角三角形，熟练掌握在网格图用勾股定理求线段长是解题的关键．

18.【答案】解：如图，△A′B′C′即为所求；
 
【解析】连接BB′，CC′交于点O，点O即为对称中心，作出点A关于点O的对称点A′即可解决问题；
本题考查旋转变换−中心对称，解题的关键是正确寻找对称中心，属于中考常考题型．

19.【答案】解：(1)∵64的立方根是m，
∴m=364=4；
(2)∵m的平方根是n，
∴n2=4，
∴ m+n2= 4+4=2 2． 
【解析】(1)根据立方根定义即可得到m的值；
(2)根据立方根及平方根定义即可得到m及n2的值，代入纠结即可得到答案．
本题考查立方根及平方根的定义，解题的关键是先求出m，再根据平方根定义得到n2的值整体代入．

20.【答案】解：∵DE//AB，
∴∠A=∠E，
在△ABC和△EDC中，
∠A=∠E∠ACB=∠ECDBC=DC，
∴△ABC≌△EDC(AAS)，
∴DE=AB．
即DE的长就是A、B两点之间的距离． 
【解析】根据两直线平行，内错角相等可得∠A=∠E，然后利用“角角边”证明△ABC和△EDC全等，根据全等三角形对应边相等解答；
本题考查了全等三角形的应用，熟练掌握三角形全等的判定方法是解题的关键．

21.【答案】① 
【解析】解：(1)第①步应先算括号里，故第①步错误．
故答案为：①；
(2)2x+1÷(2x2−1+1x+1)
=2x+1÷(2x2−1+x−1x2−1)
=2x+1÷x+1x2−1
=2x+1÷x+1(x+1)(x−1)
=2x+1÷1x−1
=2x+1×(x−1)
=2x−2x+1．
(1)根据分式混合运算的顺序解答即可；
(2)根据分式混合运算的顺序求解即可
本题考查了分式的混合运算，熟练掌握分式的运算法则是解答本题的关键．

22.【答案】解：(1)原式= 3+1−4 3+12+95×(2 3− 33)
=13−3 3+95×5 33
=13；
(2)设■=m，
则 3+(1−2 3)2−m( 12− 13)=8−3 3，
−m(2 3− 33)=8−3 3− 3−13+4 3．
−5 33m=−5．
m= 3． 
【解析】(1)先计算乘方，再计算乘法，最后计算加减即可；
(2)设■=m，则 3+(1−2 3)2−m( 12− 13)=8−3 3，求解即可．
本题考查二次根式的混合运算，解一元一次方程，熟练掌握二次根式混合运算法则是解题的关键．

23.【答案】1.25 
【解析】解：(1)设实际每天制作“冰墩墩”x个，可得方程36000.8x−10=3600x，
则n=1÷0.8=1.25，
故答案为：1.25；
(2)n=1.5时，设原计划每天制作“冰墩墩”y个，则实际每天制作“冰墩墩”1.5y个，
由题意得：3600y−36001.5y=10，
解得：y=120，
经检验，y=120是原方程的解，且符合题意，
则1.5y=1.5×120=180，
答：实际每天制作“冰墩墩”180个．
(1)由题意求出n的值即可；
(2)设原计划每天制作“冰墩墩”y个，则实际每天制作“冰墩墩”1.5y个，由题意：某玩具生产厂家接到制作3600个“冰墩墩”的订单，但是在实际制作时，结果提前10天完成，列出分式方程，解方程即可．
本题考查了分式方程的应用，找准等量关系，正确列出分式方程是解题的关键．

24.【答案】(1)证明：在△ABC中，BD、CE分别是边AC、AB上的高线，
∴∠BDC=∠CEB=90°，
在Rt△BCD和Rt△CBE中，
BD=CEBC=CB，
∴Rt△BCD≌Rt△CBE(HL)，
∴∠BCD=∠CBE，
∴AB=AC，
∴△ABC是等腰三角形；

(2)证明：在△ABC中，BD、CE分别是边AC、AB上的高线，
∴∠BDC=∠CEB=90°，
∵F是BC的中点，
∴EF=DF=12BC，
∴△DEF是等腰三角形，
∵G是ED的中点，
∴FG⊥DE；

(3)解：∵BD、CE分别是边AC、AB上的高线．
∴∠BDC=∠CEB=90°，
∵F是BC的中点，BC=16，
∴EF=DF=12BC=BF=CF=8，
∴∠BEF=∠ABC，∠CDF=∠ACB，
∵∠A=60°，
∴∠ABC+∠ACB=120°，
∴∠BFE+∠CFD=360°−2(∠ABC+∠ACB)=120°，
∴∠EFD=60°，
∴△DEF是等边三角形，
∵G是ED的中点，
∴EG=12DE=12EF=4，
∴FG= EF2−EG2= 82−42=4 3． 
【解析】(1)由在△ABC中，BD、CE分别是边AC、AB上的高线，BD=CE，利用HL可判定Rt△BCD≌Rt△CBE，则可得∠BCD=∠CBE，继而证得AB=AC；
(2)由直角三角形斜边上的中线等于斜边的一半，可判定EF=DF，可得△DEF是等腰三角形，由等腰三角形的三线合一，可证得FG⊥DE；
(3)由∠A=60°，可求得∠EFD=60°，可判定△DEF是等边三角形，根据直角三角形斜边上的中线得EF=DF=8，由等边三角形的性质即可求解．
此题是三角形综合题，考查了全等三角形的判定与性质、等腰三角形的判定与性质、等边三角形的判定与性质以及直角三角形斜边的中线的性质．此题难度适中，解题的关键是掌握数形结合思想的应用．