河北省保定市清苑区2022-2023学年七年级上学期期末数学试题（含答案）

这是一份河北省保定市清苑区2022-2023学年七年级上学期期末数学试题（含答案），共10页。试卷主要包含了本试卷共8页等内容，欢迎下载使用。

2022～2023学年度第一学期期末调研考试
七年级数学试卷
注意事项：
1．本试卷共8页．共26小题，满分120分．考试时间120分钟；
2．请用黑色钢笔、碳素笔或圆珠笔书写（作图除外）．
一、选择题（在下列各题的4个选项中，只有一项最符合题意，请把所选选项前的字母在答题卡上涂黑（共42分，1～10小题每小题3分；11～16小题，每小题2分）
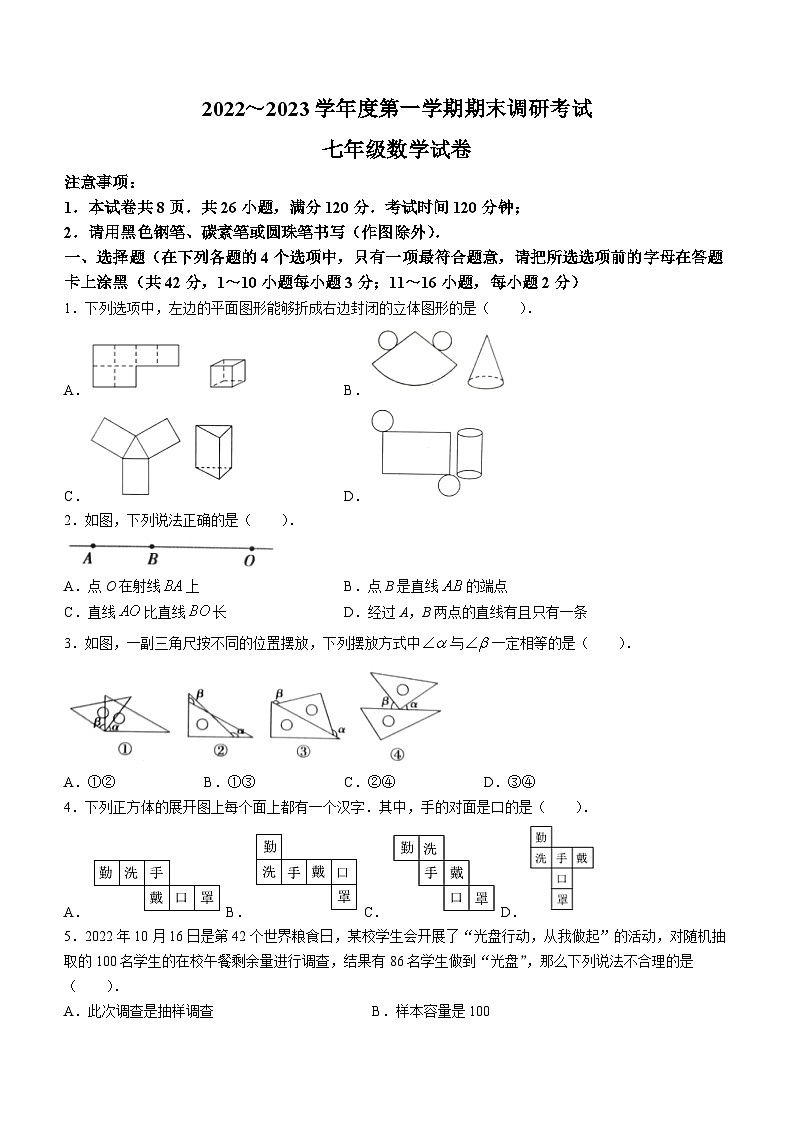
1．下列选项中，左边的平面图形能够折成右边封闭的立体图形的是（ ）．
A． B．
C． D．
2．如图，下列说法正确的是（ ）．

A．点O在射线上 B．点B是直线的端点
C．直线比直线长 D．经过A，B两点的直线有且只有一条
3．如图，一副三角尺按不同的位置摆放，下列摆放方式中与一定相等的是（ ）．

A．①② B．①③ C．②④ D．③④
4．下列正方体的展开图上每个面上都有一个汉字．其中，手的对面是口的是（ ）．
A．B．C．D．
5．2022年10月16日是第42个世界粮食日，某校学生会开展了“光盘行动，从我做起”的活动，对随机抽取的100名学生的在校午餐剩余量进行调查，结果有86名学生做到“光盘”，那么下列说法不合理的是（ ）．
A．此次调查是抽样调查 B．样本容量是100
C．全校只有14名学生没有做到“光盘” D．全校约有86％的学生做到“光盘”
6．若，则在①；②；③；④中，正确的有（ ）．
A．1个 B．2个 C．3个 D．4个
7．用代数式表示“x与y的2倍的和”是（ ）．
A． B． C． D．
8．“精准扶贫”以来，农村贫困人口收入逐年上升，某村民近两年的年收入发生了明显变化，已知前年和去年的收入分别是40000元和60000元，如图是依据①②③三种农作物每种作物每年的收入占该年年收入的比例绘制的扇形统计图．依据统计图得出的以下四个结论正确的是（ ）．

A．①的收入去年和前年相同 B．③的收入所占比例前年的比去年的大
C．去年②的收入为2.1万元 D．前年年收入不止①②③三种农作物的收入
9．中国华为麒麟985处理器是采用7纳米制程工艺的手机芯片，在指甲盖大小的芯片上集成了12000000000个晶体管，是目前世界上最先进的具有人工智能的手机处理器．请将数字12000000000用科学记数法表示为（ ）．
A． B． C． D．
10．如图是小明同学当堂检测填空题的完成情况，他最后的得分是（ ）．
姓名 小明 得分______
填空题（评分标准：每道题4分）
（1）
（2）
（3）
（4）
A．4分 B．8分 C．12分 D．16分
11．是下列方程的解的有（ ）．
①；②；③；④．
A．1个 B．2个 C．3个 D．4个
12．下列变形中正确的是（ ）．
A．方程，移项，得
B．方程，去括号，得
C．方程，未知数系数化为1，得
D．方程化为
13．如图，两个面积分别为10，17的图形叠放在一起，两个阴影部分的面积分别为a，，则的值为（ ）．

A．7 B．14 C． D．
14．相传有个人不讲究说话艺术常引起误会，一天他设宴请客，他看到几个人没来，就自言自语：“怎么该来的还不来呢？”客人听了，心想难道我们是不该来的，于是已到的客人的一半走了，他一看十分着急，又说：“嗨，不该走的倒走了！”剩下的人一听，是我们该走啊！又有剩余客人的三分之一离开了，他着急地一拍大腿：“我说的不是他们．”于是剩下的6个人也走了，聪明的你知道最开始来了多少客人吗？
A．16 B．18 C．20 D．22
15．如图，，是内任意一条射线，，分别平分，，有下列结论：①；②；③；④．其中正确的是（ ）．

A．①②④ B．①③④ C．①②③ D．②③④
16．如图所示的图形都由同样大小的小圆圈按一定规律所组成的，若按此规律排列下去，则第50个图形中有（ ）个小圆圈．

A．2454 B．2605 C．2504 D．2554
二、填空题（本大题共3个小题，共9分．17，18每小题3分，19小题每空1分）
17．小明在用玩具枪瞄准时，总是用一只眼对准准星和目标，用数学知识解释为：__________．
18．有理数a，b在数轴上对应的点如图所示，若，且，则a的值是__________．

19．定义一种对正整数n的“F运算”：①当n为奇数时，结果为；②当n为偶数时，结果为（其中k是使为奇数的正整数），并且运算重复进行，例如，取，第三次“F运算”的结果是11．
若，
（1）第一次“F运算”的结果为__________；第二次“F运算”的结果为__________；
（2）照这样运算下去，第2022次“F运算”的结果为__________．
三、解答题（本大题7个小题，共69分．解答应写出文字说明、证明过程或演算步骤）
20．（每小题5分，共20分）
（1）计算：．
（2）．
（3）解方程：．
（4）先化简再求值：求多项式的值，其中，．
21．（本小题满分8分）
在学习《展开与折叠》这一课时，老师让同学们将准备好的正方体或长方体沿某些棱剪开，展开成平面图形．其中，小明同学不小心多剪了一条棱，把一个长方体纸盒剪成了图1、图2两部分．根据你所学的知识，回答下列问题：

（1）小明共剪开了几条棱？
（2）现在，小明将剪断的图2重新粘贴到图1上去，而且经过折叠以后，仍然可以还原成一个长方体纸盒，他有几种粘贴方法？请在图1上画出粘贴后的图形（画出一种即可）．
（3）已知图3是小明剪开的图1的某些数据，求这个长方体纸盒的体积．
22．（本小题满分8分）
学习完统计知识后，小明就本班同学的上学方式进行调查统计，如图是他通过收集数据后所绘制的两幅不完整的统计图，请你根据图中提供的信息解决下列问题：

（1）求该班共有多少名学生？
（2）请将表示“步行”部分的条形统计图补充完整；
（3）在扇形统计图中，“骑车”部分扇形所对应的圆心角是多少度？
（4）若全年级共有1000名学生，估计全年级骑车上学的学生有多少名？
23．（本小题满分8分）
课上，老师提出问题：如图，点O是线段上一点，C，D分别是线段，的中点，当时，求线段的长度．
（1）下面是小明根据老师的要求进行的分析及解答过程，请你补全解答过程；
思路方法
解答过程
知识要素
未知线段
转化
已知线段
因为C，D分别是线段，的中点，
所以，__________，
因为，
所以______＝______＝______．

线段中点的定义
线段的和、差
等式的性质
（2）小明进行题后反思，提出新的问题：如果点O运动到线段的延长线上，的长度是否会发生变化？请你帮助小明作出判断并说明理由．
24．（本小题满分8分）
将正方形（如图1）作如下划分，第1次划分：分别连接正方形对边的中点（如图2），得线段和，它们交于点M，此时图2中共有5个正方形；第2次划分：将图2左上角正方形再划分，得图3，则图3中共有9个正方形；

（1）若把左上角的正方形依次划分下去，则第5次划分后，图中共有______个正方形．
（2）继续划分下去，第n次划分后图中共有______个正方形；
（3）能否将正方形划分成有2022个正方形的图形？如果能，请算出是第几次划分，如果不能，需说明理由．
（4）如果设原正方形的边长为1，通过不断地分割该面积为1的正方形，并把数量关系和几何图形巧妙地结合起来，可以很容易得到一些计算结果，试着探究求出下面表达式的结果．
（直接写出答案即可）
25．（本小题满分9分）
某班进行了“庆祝建党101周年知识竞赛”活动，班长安排小明购买奖品，如图两幅图是小明买回奖品时与班长的对话情况：

请根据图13-1、图13-2的信息，解答下列问题：
（1）小明买了两种笔记本各多少本？（要求列一元一次方程解决问题）
（2）为什么班长说不可能找回68元钱，请说明理由．
26．（本小题满分8分）
如图，已知，射线从的位置开始绕点O按顺时针方向旋转，速度是每秒，同时射线从的位置开始绕点O按逆时针方向旋转，速度是每秒，设旋转时间为t秒．

（1）用含t的代数式表示和的度数；
（2）在旋转过程中，当等于时，求t的值；
（3）在旋转过程中是否存在这样的t，使得射线恰好是图中某个角的平分线？如果存在，请求出t的值；如果不存在，请说明理由．





2022～2023第一学期期末考试七年级数学答案
注意事项：解答题部分答案不唯一．
一、选择题（共42分，1～10小题每小题3分；11～16小题，每小题2分）
题号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
答案
D
D
B
B
C
C
B
C
C
C
C
D
B
B
A
D
二、填空题（17，18每小题3分，19小题每空1分，共9分）
17．两点确定一条直线（或“经过两点有且只有一条直线”）．
18．
19．（1）338；169 （2）1
三、解答题（本大题共6个小题，共68分）
20．（每小题5分，共20分）
解：（1）原式（5分）
（2）原式（10分）
（3）解：去分母，得，（12分）
去括号，得，（13分）
移项、合并同类项，得，（14分）
方程两边同除以2得．（15分）
（4）原式（18分）
当，时，原式．（20分）
21．解：（1）总共12条棱，其中4条棱未剪开，
所以小明总共剪开了8条棱．（2分）
（2）有4种粘贴方法（3分）
如图所示：（画出其中一种即可）
（5分）
（3）由图可知，长方体的长为，宽为，高为，
∴长方体的体积为：（8分）
22．解（1）％＝40（名）
答：该班共有40名学生．（2分）
（2）“步行”学生人数：％＝8（名），补全图形，如图所示：
（4分）
（3）“骑车”部分扇形所对应的圆心角的度数：（1－50％－20％）．（6分）
（4）1000×（1－50％－20％）＝300（名）
答：估计全年级骑车上学的学生有300名．（10分）
23．解：（1）解答过程：因为C，D分别是线段，的中点，
所以，，
因为，所以．（4分）
（2）不会发生变化，理由如下：（5分）

∵C，D分别是线段，的中点，所以，，
又∵，∴．（8分）
24．解：（1）21（2分）
（2）（4分）
（3）不能，理由：由，解得，n不是整数，
所以不能将正方形划分成2022个正方形的图形．（6分）
（4）（8分）
25．解：（1）设5元的笔记本买了x本，8元的笔记本买了本，
根据题意，得，（3分）
解这个方程，得，（本）．
答：5元的笔记本买了25本，8元的笔记本买了15本．（6分）
（2）假设找回的钱数是68元，设5元的笔记本买了x本，8元的笔记本买了本，
根据题意，得，
解这个方程，得，x不是整数，不符合题意，
∴小明找回的钱不可能是68元．（9分）
26．解：（1）的度数为度，的度数为度．（2分）
（2）
①如图1，．
，解得．（3分）
②如图2，．
．解得．
∴当时，t的值为6或18．（5分）
（3）①当平分时，，解得；
②当平分时，，解得；
③当平分时，，解得．
综上所述，当或15或10时，射线恰好是图中某个角的平分线．（8分）