

湖南省宁乡市2022-2023学年高二下学期学业水平合格性考试数学模拟试卷(含答案)
展开2022-2023学年学业水平合格性考试模拟试卷
数 学
一、选择题(共18题,共54分)
1. 已知集合 ,且 ,则 的值可能为
A. B. C. D.
2. 与 角的终边相同的角是
A. B. C. D.
3. 命题“,”的否定是
A. , B. ,
C. , D. ,
4. 一正方体的六个面上用记号笔分别标记了一个字,已知其表面展开图如图所示,则在原正方体中,互为对面的是
A.西与楼,梦与游,红与记 B.西与红,楼与游,梦与记
C.西与楼,梦与记,红与游 D.西与红,楼与记,梦与游
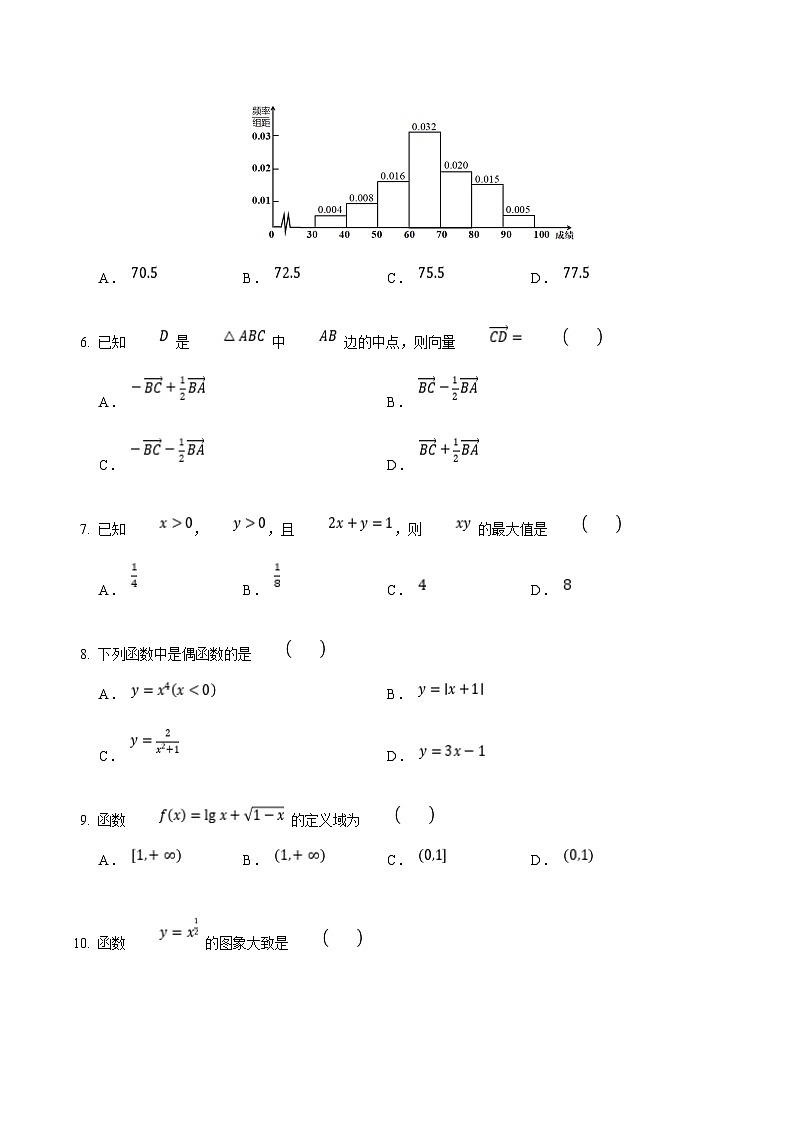
5. 某公司计划招收 名新员工,共报名了 人,远超计划,故该公司采用笔试的方法进行选拔,并按照笔试成绩择优录取.现采用随机抽样的方法抽取 名报名者的笔试成绩,绘制频率分布直方图如下,则录取分数线可估计为
A. B. C. D.
6. 已知 是 中 边的中点,则向量
A. B.
C. D.
7. 已知 ,,且 ,则 的最大值是
A. B. C. D.
8. 下列函数中是偶函数的是
A. B.
C. D.
9. 函数 的定义域为
A. B. C. D.
10. 函数 的图象大致是
A. B.
C. D.
11. 设复数 满足 ,则
A. B. C. D.
12. 已知一只口袋内装有大小相同的 只球,其中 只白球, 只黑球,从中一次摸出 只球,则摸出的 只球中至少有 只是白球的概率是
A. B. C. D.
13. 已知 ,且 ,则
A. B. C. D.
14. 高铁、扫码支付、共享单车、网购被称为中国的“新四大发明”,为评估共享单车的使用情况,选了 座城市作试验基地,这 座城市共享单车的使用量(单位;人次/天)分别为 ,,,,下面给出的指标中可以用来评估共享单车使用量的稳定程度的是
A. ,,, 的平均数 B. ,,, 的标准差
C. ,,, 的最大值 D. ,,, 的中位数
15. 在实数集上定义运算 :.若不等式 对任意实数 都成立,则实数 的取值范围是
A. B. C. D.
16. 某公司为激励创新,计划逐年加大研发资金投入.若该公司2015年全年投入研发资金 万元,在此基础上每年投入的研发资金比上一年增长 ,则该公司全年投入的研发资金开始超过 万元的年份是
(参考数据:,,)
A.2018年 B.2019年 C.2020年 D.2021年
17. 如图,在下列四个正方体中,, 为正方体的两个顶点,,, 为所在棱的中点,则在这四个正方体中,直线 与平面 不垂直的是
A. B.
C. D.
18. 已知函数 ,给出下列结论:
① 的最小正周期为 ;
② 在区间 上是增函数;
③ 的图象关于直线 对称;
④把函数 的图象上所有点向左平移 个单位长度,可得到函数 的图象.
其中正确结论的个数是
A. B. C. D.
二、填空题(共4题,共12分)
19. .
20. 已知一扇形的弧所对的圆心角为 ,半径 ,则扇形的周长为 .
21. 某圆锥体的底面圆的半径长为 ,其侧面展开图是圆心角为 的扇形,则该圆锥体的体积是 .
22. 《镜花缘》是清代文人李汝珍创作的长篇小说,书中有这样一个情节:一座楼阁到处挂满了五彩缤纷的大小灯球,灯球有两种,一种是大灯下缀 个小灯,另一种是大灯下缀 个小灯,大灯共 个,小灯共 个.若在这座楼阁的灯球中,随机选取一个灯球,则这个灯球是大灯下缀 个小灯的概率为 .
三、解答题(共3题,共34分)
23. 如图,已知正方体 的棱长为 ,, 分别是棱 与 的中点.
(1) 求以 ,,, 为顶点的四面体的体积;
(2) 求异面直线 和 所成的角的大小.
24. 已知函数 .
(1) 求 的值;
(2) 求 的最小正周期;
(3) 求函数 的单调递减区间.
25. 已知函数 .
(1) 若函数 的最大值为 ,求实数 的值.
(2) 若函数 在 上单调递减,求实数 的取值范围.
(3) 是否存在实数 ,使函数 在区间 上的值域也为 ?若存在,求出 的值,若不存在,请说明理由.
参考答案
1-18 CADBD ABCCB DDBBC BDB
19. M20. 21. 22.
23.
(1) 该四面体是以 为底面, 为顶点的三棱锥,
到平面 的距离 ,
的面积 ,
因此四面体 的体积 .
(2) 以 为原点, 方向为 轴正方向, 方向为 轴正方向, 方向为 轴正方向建立空间直角坐标系.
得 ,,,,
故 ,,
设 与 所成的角的大小为 ,
则 ,
故 与 所成的角的大小为 .
24.
(1)
.
(2) 由 , 的最小正周期 .
(3) 函数 的单调递减区间为 ,
由 ,得 ,
函数 的单调递减区间为 .
25.
(1) 因为 ,开口向下,对称轴 ,,
所以 ,解得 或 .
(2) 若函数 在 上单调递减,则 ,解得 ,
所以 的取值范围是 .
(3) ,开口向下,
对称轴 , 在 上的值域为 ,
当 时, 在 上是减函数,
所以 即 解得 不存在,
当 时, 在 上是增函数,
所以 即 解得 ,
当 时, 在 是增函数,在 是减函数,
所以 ,解得 或 (舍),
综上,存在实数 ,使 在区间 上的值域为 .
2023年湖南省普通高中学业水平合格性考试数学模拟试题(二): 这是一份2023年湖南省普通高中学业水平合格性考试数学模拟试题(二),共6页。
2021-2022学年福建省普通高中高二学业水平合格性考试数学模拟试题(解析版): 这是一份2021-2022学年福建省普通高中高二学业水平合格性考试数学模拟试题(解析版),共14页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
2022年湖南省普通高中学业水平合格性考试数学模拟试卷: 这是一份2022年湖南省普通高中学业水平合格性考试数学模拟试卷,共4页。












