

2022-2023学年广东省广州市天河区七年级(下)期末数学试卷(含解析)
展开2022-2023学年广东省广州市天河区七年级(下)期末数学试卷
学校:___________姓名:___________班级:___________考号:___________
第I卷(选择题)
一、选择题(本大题共8小题,共24.0分。在每小题列出的选项中,选出符合题目的一项)
1. 下列调查方式,你认为最合适全面调查的是( )
A. 调查某地全年的游客流量 B. 乘坐地铁前的安检
C. 调查某种型号灯泡的使用寿命 D. 调查春节联欢晚会的收视率
2. 下列选项中,无理数的是( )
A. −12 B. |−2| C. 3 D. 0
3. 在平面直角坐标系中,下列各点在第四象限的是( )
A. (−1,−2) B. (1,−2) C. (1,2) D. (−1,2)
4. 若a
A. 10°
B. 30°
C. 35°
D. 20°
6. 已知方程2mx−y=10的一组解为x=1y=2,则m的值是( )
A. 6 B. 16 C. 4 D. 14
7. 不等式x<32x>−1的整数解是( )
A. 0,1 B. −1,0 C. −1,0,1 D. 无解
8. 有四位同学一起研究一道数学题,已知条件是:如图,F,G分别是三角形ABC的边BC和AC上的一点,CD⊥AB,EF⊥AB,垂足分别为D,E,连接DG.则他们的说法错误的是( )
A. 甲说:“如果还知道∠CDG=∠BFE,则能得到∠AGD=∠ACB.
B. 乙说:“如果还知道∠AGD=∠ACB,则能得到∠CDG=∠BFE.
C. 丙说:“如果还知道∠ADG=∠AGD,则能得到∠EBF=∠ACB.”
D. 丁说:“如果还知道DG//BC,则能得到∠CDG=∠BFE.”
二、多选题(本大题共2小题,共10.0分。在每小题有多项符合题目要求)
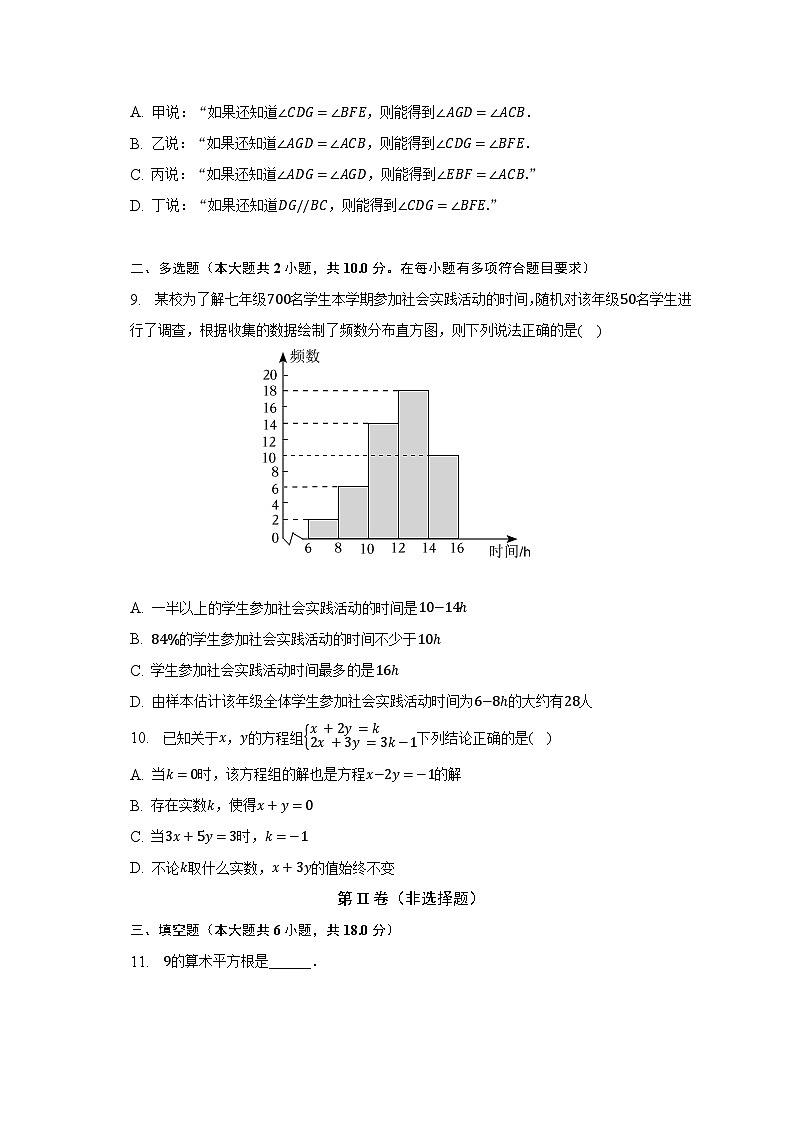
9. 某校为了解七年级700名学生本学期参加社会实践活动的时间,随机对该年级50名学生进行了调查,根据收集的数据绘制了频数分布直方图,则下列说法正确的是( )
A. 一半以上的学生参加社会实践活动的时间是10−14h
B. 84%的学生参加社会实践活动的时间不少于10h
C. 学生参加社会实践活动时间最多的是16h
D. 由样本估计该年级全体学生参加社会实践活动时间为6−8h的大约有28人
10. 已知关于x,y的方程组x+2y=k2x+3y=3k−1下列结论正确的是( )
A. 当k=0时,该方程组的解也是方程x−2y=−1的解
B. 存在实数k,使得x+y=0
C. 当3x+5y=3时,k=−1
D. 不论k取什么实数,x+3y的值始终不变
第II卷(非选择题)
三、填空题(本大题共6小题,共18.0分)
11. 9的算术平方根是______.
12. 七年级三班座位按7排8列排列,王东的座位是3排4列,简记为(3,4),张三的座位是5排2列,可简记为______.
13. x的2倍与5的差是负数,用不等式表示为______.
14. 一组数据,其中最大值是177cm,最小值是154cm,对这种数进行整理时,若取组距为3,则适合的组数是______ .
15. 如图所示,直线l//m,将含有45°角的三角形板ABC的直角顶点C放在直线m上.若∠1=25°,则∠2的度数为______.
16. 阅读下列材料:因为 4< 5< 9,即2< 5<3,所以 5的整数部分为2,小数部分为 5−2,若规定实数m的整数部分记为[m],小数部分记为{m},可得[ 5]=2,{ 5}= 5−2.按照此规定计{5− 5}的值是______ .
四、计算题(本大题共1小题,共6.0分)
17. 解方程组:2x+y=4x−y=−1.
五、解答题(本大题共7小题,共62.0分。解答应写出文字说明,证明过程或演算步骤)
18. (本小题6.0分)
(1)计算 4−327;
(2)解不等式3(x−1)>2x,并在数轴上表示解集.
19. (本小题8.0分)
如图,AD是∠EAC的平分线,AD//BC,∠B=30°,求∠C的度数.
20. (本小题8.0分)
学校社团活动可以丰富学生的课余生活,陶冶学生的情趣和爱好,某校为了解七年级200名学生参加不同社团分类的情况,开展了抽样调查,并根据抽样数据制作出如图所示的两个不完整统计图,根据图中信息完成以下问题:
(1)填空:
①这次调查的学生人数是______ ;
②在扇形统计图中,表示“书法类”所在扇形圆心角的度数是______ ;
(2)估算七年级全体学生参加艺术类社团的学生人数.
21. (本小题9.0分)
如图,在平面直角坐标系中,将△ABC先向左平移1个单立长度,再向下平移6个单位长度,得到Δ A′B′C′.
(1)画出△A′B′C′;
(2)连接A′B,A′C,求△A′BC和△A′B′C′的面积差.
22. (本小题9.0分)
“广交会”是我国目前历史最长,规模最大的综合性国际贸易盛会,第133届“广交会”于2023年4月15日开幕,某参展商需要用大小两种货车运货,1辆大货车与1辆小货车一次可以运货6吨,2辆大货车与3辆小货车一次可以运货14吨,问:每辆大货车与小货车一次分别可以运货多少吨?
23. (本小题10.0分)
对于两个数a,b,我们定义:
①M(a,b)表示这两个数的平均数,例如M(−1.3)=−1+32=1;
②max(a,b)表示这两个数中更大的数,当a≥b时,max(a,b)=a;当a
(2)已知max{−2x+5,−1}=−2x+5,求x的取值范围;
(3)已知M(4x+y,y)=max(0,1)M(5−2x,1)=M(x,x−2y),求x和y的值.
24. (本小题12.0分)
已知点A(−2,0),B(0,−4),C(−4,−6),过点C作x轴的平行线m,交y轴于点D,一动点P从C点出发,在直线m上以1个单位长度/秒的速度向右运动.
(1)如图,当点P在第四象限时,连接OP,作射线OE平分∠AOP,过点O作OF⊥OE.
①填空:若∠OPD=60°,则∠POF= ______ ;
②设a=∠OPD∠DOE,求a的值.
(2)若与此同时,直线m以2个单位长度/秒的速度竖直向上运动,设运动时间为t秒,点P的坐标为(x,y).
①在坐标轴上是否存在满足条件的点P,使得S△ABP=6.若存在,求出点P的坐标;若不存在,请说明理由;
②求x和y的关系式.
答案和解析
1.【答案】B
【解析】解:A.调查某地全年的游客流量,适合抽样调查,故本选项不合题意;
B.乘坐地铁前的安检,适合采用全面调查方式,故本选项符合题意;
C.调查某种型号灯泡的使用寿命,适合抽样调查,故本选项不合题意;
D.调查春节联欢晚会的收视率,适合抽样调查,故本选项不合题意;
故选:B.
根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似进行判断.
此题考查全面调查与抽样调查,关键是根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似进行判断.
2.【答案】C
【解析】解:A.−12是分数,属于有理数,故本选项不符合题意;
B.|−2|=2,是整数,属于有理数,故本选项不符合题意;
C. 3是无理数,故本选项符合题意;
D.0是整数,属于有理数,故本选项不符合题意.
故选:C.
根据无理数的定义(无限不循环小数叫做无理数),即可得到答案.
本题考查无理数,掌握无理数的定义是解答本题的关键.
3.【答案】B
【解析】解:A、(−1,−2)在第三象限,故本选项不符合题意;
B、(1,−2)在第四象限,故本选项符合题意;
C、(1,2)在第一象限,故本选项不符合题意;
D、(−1,2)在第二象限,故本选项不符合题意.
故选:B.
根据各象限点的坐标的特点解答.
本题考查了点的坐标.熟记各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(−,+);第三象限(−,−);第四象限(+,−).
4.【答案】C
【解析】解:A、不等式a
D、不等式a
根据不等式的性质分析判断.
本题主要考查了不等式的性质.解题的关键是掌握不等式的性质:(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变;(2)不等式两边乘(或除以)同一个正数,不等号的方向不变;(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.
5.【答案】D
【解析】解:∵AB⊥CD,
∴∠AOD=90°,
∴∠AOE=∠AOD−∠EOD=90°−70°=20°.
∴∠BOF=∠AOE=20°.
故选:D.
根据垂线及各角之间的关系求解即可.
本题考查垂线,比较简单,直接计算即可.
6.【答案】A
【解析】解:∵x=1,y=2是方程2mx−y=10的一组解,
∴将x=1,y=2代入方程2mx−y=10,得2m−2=10,解得m=6.
故选:A.
将方程的解x=1,y=2代入方程,得到关于m的一元一次方程,解得m值即可.
本题考查二元一次方程的解,比较简单,重点是理解方程与解之间的关系.
7.【答案】A
【解析】解:∵x<32x>−1,
∴不等式组的解集为−1
故选:A.
根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集.
本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
8.【答案】C
【解析】解:A、∵CD⊥AB,EF⊥AB,
∴CD//EF,
∴∠BCD=∠BFE,
∵∠CDG=∠BFE,
∴∠BCD=∠CDG,
∴DG//BC,
∴∠AGD=∠ACB,
∴甲的说法正确,
故此选项不符合题意;
B、∵CD⊥AB,EF⊥AB,
∴CD//EF,
∴∠BCD=∠BFE,
∵∠AGD=∠ACB,
∴DG//BC,
∴∠BCD=∠CDG,
∴∠CDG=∠BFE,
∴乙的说法正确,
故此选项不符合题意;
C、由∠ADG=∠AGD,不能得到∠EBF=∠ACB,
∴丙的说法错误,
故此选项符合题意;
D、∵CD⊥AB,EF⊥AB,
∴CD//EF,
∴∠BCD=∠BFE,
∵DG//BC,
∴∠CDG=∠BCD,
∴∠CDG=∠BFE,
∴丁的说法正确,
故此选项不符合题意;
故选:C.
由已知条件可证得CD//EF,得出∠BCD=∠BFE,当添加∠CDG=∠BFE时,利用等量代换得出∠BCD=∠CDG,于是有DG//BC,即可得出∠AGD=∠ACB;当添加∠AGD=∠ACB时,根据同位角相等,两直线平行得出DG//BC,于是有∠CDG=∠BCD,从而得出∠CDG=∠BFE;当添加∠ADG=∠AGD时,无法得出∠EBF=∠ACB;当添加DG//BC时,可得出∠CDG=∠BCD,从而得出∠CDG=∠BFE.
本题考查了平行线的性质与判定,能灵活运用定理进行推理是解题的关键.
9.【答案】ABD
【解析】解:A、参加社会实践活动的时间是10−14h所占的百分比为14+1850=64%,故符合题意;
B、参加社会实践活动的时间不少于10h所占的百分比为50−2−650=84%,故符合题意;
C、最后一个小组的时间范围为14~16h,但不代表一定有活动时间为16h的同学,故不符合题意;
D、由样本估计该年级全体学生参加社会实践活动时间为6−8h的大约有700×250=28人,故符合题意;
故选:ABD.
阅读频数分布直方图,根据直方图中获取的信息进行判断即可.
本题主要考查的是频数(率)分布直方图和用样本估计总体,能够从直方图中获取有效信息是解题的关键.
10.【答案】BD
【解析】解:当k=0时,方程组为x+2y=0①2x+3y=−1②.
将①的左右两边同时乘以2,得2x+4y=0③.
③−②得y=1.
将y=1代入①,得x+2=0,解得x=−2.
当x=−2,y=1时,x−2y=−2−2=−4.
∴当k=0时,该方程组的解不是方程x−2y=−1的解.
故A不符合题意.
将各方程左右两边分别相减,得x+y=2k−1.
当x+y=0时,有2k−1=0,解得k=12.
故B符合题意.
将各方程左右两边分别相加,得3x+5y=4k−1.
当3x+5y=3时,有4k−1=3,解得k=1.
故C不符合题意.
将方程x+2y=k左右两边同时乘以−3,得−3x−6y=−3k,
将它与方程2x+3y=3k−1左右两边分别相加,得−x−3y=−1,即x+3y=1.
故D符合题意.
故答案为:BD.
对四个选项分别分析判断即可.
本题考查二元一次方程和二元一次方程组的解,需要对四个选项分别分析判断,所以要求有一定的计算能力,做到快速、正确.
11.【答案】3
【解析】解:因为32=9,
所以9的算术平方根是3.
故答案为:3.
根据算术平方根的定义解答即可.
本题考查了数的算术平方根,解题的关键是牢记算术平方根为非负数.
12.【答案】(5,2)
【解析】解:∵王东的座位是3排4列,简记为(3,4),
∴张三的座位是5排2列,可简记为(5,2).
故答案为:(5,2).
根据有序数对的第一个数表示排数,第二个数表示列数解答.
本题考查了坐标确定位置,理解有序数对的两个数的实际意义是解题的关键.
13.【答案】2x−5<0
【解析】解:∵x的2倍与5的差是负数,
∴2x−5<0,
故答案为:2x−5<0.
根据x的2倍与5的差是负数可得不等式.
本题考查了不等式的应用,能根据题意列出不等关系是解题的关键.
14.【答案】8
【解析】解:(177−154)÷3=723,
即适合的组数是8.
故答案为:8.
求出最大值与最小值的差,再根据组距、组数、极差的关系进行计算即可.
本题考查频数分布表,调查收集数据的过程与方法,掌握组距、组数、极差之间的关系是正确计算的前提.
15.【答案】20°
【解析】解:如图,过点B作BD//l.
∵直线l//m,
∴BD//l//m,
∴∠4=∠1=25°,
∵∠ABC=45°,
∴∠3=∠ABC−∠4=45°−25°=20°,
∴∠2=∠3=20°.
故答案为:20°.
首先过点B作BD//l,由直线l//m,可得BD//l//m,由两直线平行,内错角相等,即可求得答案∠4的度数,又由△ABC是含有45°角的三角板,即可求得∠3的度数,继而求得∠2的度数.
此题考查了平行线的性质.此题难度不大,注意辅助线的作法,注意掌握两直线平行,内错角相等定理的应用.
16.【答案】3− 5
【解析】解:{5− 5}=5− 5−2=3− 5.
故答案为:3− 5.
根据题意即可得到5− 5的小数部分.
此题考查了二次根式的化简求值,估算无理数的大小,注意首先估算无理数的值,再根据不等式的性质进行计算.
17.【答案】解:2x+y=4①x−y=−1②,
①+②得:3x=3,即x=1,
把x=1代入①得:y=2,
则方程组的解为x=1y=2.
【解析】本题主要考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.熟练掌握解二元一次方程组的方法是解题的关键.
方程组利用加减消元法求出解即可.
18.【答案】解:(1)原式=2−3
=−1;
(2)3(x−1)>2x,
3x−3>2x,
3x−2x>3,
x>3,
在数轴上表示不等式的解集是:
.
【解析】(1)分别根据算术平方根和立方根的定义计算即可;
(2)去括号,移项,合并同类项,系数化成1,最后在数轴上表示出来即可.
本题考查了实数的运算,掌握相关定义以及不等式的性质是解答本题的关键.
19.【答案】解:∵AD//BC,
∴∠1=∠B,
∠2=∠C,
又∵AD平分∠EAC,
∴∠1=∠2,
∴∠C=∠B=30°.
【解析】首先根据平行线的性质可得∠1=∠B,∠2=∠C,再根据AD是∠EAC的平分线,可得∠1=∠2.利用等量代换可得∠B=∠C=30°.
此题主要考查了平行线的性质,以及角平分线的性质,关键是掌握平行线性质定理:
定理1:两直线平行,同位角相等;
定理2:两直线平行,同旁内角互补;
定理3:两直线平行,内错角相等.
20.【答案】50 72°
【解析】解:(1)①这次调查的学生人数是:20÷40%=50(名);
②表示“书法类”所在扇形圆心角的度数是:360°×1050=72°;
故答案为:①50;②72°;
(2)艺术的人数为50−(20+10+15)=5(名),
200×550=20(人),
答:估计七年级全体学生参加艺术类社团的学生人数为20人.
(1)①由体育类的人数除以所占的百分比即可求出调查的总学生数;②由书法类的人数除以总人数求出百分比,乘以360°即可得到结果;
(2)用总人数乘艺术类社团的百分比即可得到结果.
此题考查了条形统计图,扇形统计图,以及用样本估计总体,弄清题意是解本题的关键.
21.【答案】解:(1)如图,
△A′B′C′即为所求;
(2)∵△A′BC的面积为12×5×4=10,△A′B′C′的面积为12×5×2=5,
∴△A′BC和△A′B′C′的面积差为10−5=5.
【解析】(1)根据平移的性质作图即可;
(2)利用三角形的面积公式计算即可.
本题主要考查坐标与图形变化−平移,熟练掌握平移变换的定义和性质及三角形面积公式是解题的关键.
22.【答案】解:设每辆大货车一次可以运货x吨,每辆小货车一次可以运货y吨,
根据题意得:x+y=62x+3y=14,
解得:x=4y=2.
答:每辆大货车一次可以运货4吨,每辆小货车一次可以运货2吨.
【解析】设每辆大货车一次可以运货x吨,每辆小货车一次可以运货y吨,根据“1辆大货车与1辆小货车一次可以运货6吨,2辆大货车与3辆小货车一次可以运货14吨”,可列出关于x,y的二元一次方程组,解之即可得出结论.
本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
23.【答案】2023 2024
【解析】解:(1)由题意可得,
M(2022,2024)=2022+20242=2023,max(2023,2024)=2024,
故答案为:2023,2024;
(2)∵max{−2x+5,−1}=−2x+5,
∴−2x+5≥−1,
∴x≤3;
(3)由题意得4x+y+y2=15−2x+12=x+x−2y2,
整理得2x+y=1①2x−y=2②,
①+②得:4x=3,
解得:x=34,
①−②得:2y=−1,
解得:y=−12.
(1)根据题意,可以得到M(2020,2024)和max(2023,2024)的值;
(2)根据题意得到关于x的不等式,解不等式即可;
(3)由题意得出关于x、y的方程组,解方程组即可.
本题考查算术平均数、解一元一次不等式组,不等式的性质,解答本题的关键是明确题意,利用新定义解答.
24.【答案】30°
【解析】解:(1)①∵直线m//x轴,∠OPD=60°,
∴∠AOP+∠OPD=180°,
∴∠AOP=180°−60°=120°,
∵OE平分∠AOP,
∴∠EOP=12∠AOP=60°,
∵OF⊥OE,
∴∠EOF=90°,
∴∠POF=90°−∠EOP=90°−60°=30°,
故答案为:30°;
②∵∠AOP=∠AOD+∠DOP=90°+∠DOP,OE平分∠AOP,
∴∠EOP=12∠AOP=12(90°+∠DOP)=45°+12∠DOP,
∴∠DOE=∠EOP−∠DOP=45°+12∠DOP−∠DOP=45°−12∠DOP,
∵∠OPD=90°−∠DOP,
∴a=∠OPD∠DOE=90°−∠DOP45∘−12∠DOP=2,
即a的值为2;
(2)①在坐标轴上存在满足条件的点P,理由如下:
由题意可知,经过t秒后,点P的坐标为(−4+t,−6+2t),
a、若点P在y轴上,则−6+2t=0,
解得:t=3,
∴p(−1,0),
∴BP=3,OA=2,
∴S△ABP=12BP⋅OA=12×3×2=3≠6,不合题意;
b、若点P在y轴上,则−4+t=0,
解得:t=4,
∴P(0,2),
∴BP=6,OA=2,
∴S△ABP=12BP⋅OA=12×6×2=6,符合题意;
综上所述,在坐标轴上存在满足条件的点P,使得S△ABP=6,点P的坐标为(0,2);
②由①可知,x=−4+t,y=−6+2t,
∴t=x+4,
把t=x+4代入y=−6+2t得:y=−6+2(x+4)=2x+2,
即x和y的关系式为y=2x+2.
(1)①由平行线的性质得∠AOP=120°,再由角平分线定义得∠EOP=60°,然后由直角三角形的性质即可得出结论;
②由三角形的外角性质和角平分线定义得∠EOP=45°+12∠DOP,则∠DOE=45°−12∠DOP,再由直角三角形的性质得∠OPD=90°−∠DOP,即可得出结论;
(2)①经过t秒后,点P的坐标为(−4+t,−6+2t),再分两种情况,点P在y轴上和点P在y轴上,分别求出t的值,即可解决问题;
②由①可知,x=−4+t,y=−6+2t,则t=x+4,把t=x+4代入y=−6+2t即可得出结论.
本题是三角形综合题目,考查了平行线的性质、角平分线定义、坐标与图形性质、直角三角形的性质、三角形的外角性质、三角形面积以及分类讨论等知识,本题综合性强,熟练掌握平行线的性质和角平分线定义是解题的关键.
2022-2023学年广东省广州市天河区七年级(下)期末数学试卷(含解析): 这是一份2022-2023学年广东省广州市天河区七年级(下)期末数学试卷(含解析),共17页。试卷主要包含了选择题,多选题,填空题,计算题,解答题等内容,欢迎下载使用。
2022-2023学年广东省广州市天河区七年级(下)期末数学试卷(含解析): 这是一份2022-2023学年广东省广州市天河区七年级(下)期末数学试卷(含解析),共17页。试卷主要包含了选择题,多选题,填空题,计算题,解答题等内容,欢迎下载使用。
2022-2023学年广东省广州市天河区八年级(下)期末数学试卷(含解析): 这是一份2022-2023学年广东省广州市天河区八年级(下)期末数学试卷(含解析),共21页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。













