
2023年山东省济南市中考数学三模试卷(含解析)
展开2023年山东省济南市中考数学三模试卷
一、选择题(本大题共10小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
1. −32的倒数是( )
A. |−23| B. −23 C. −112 D. 32
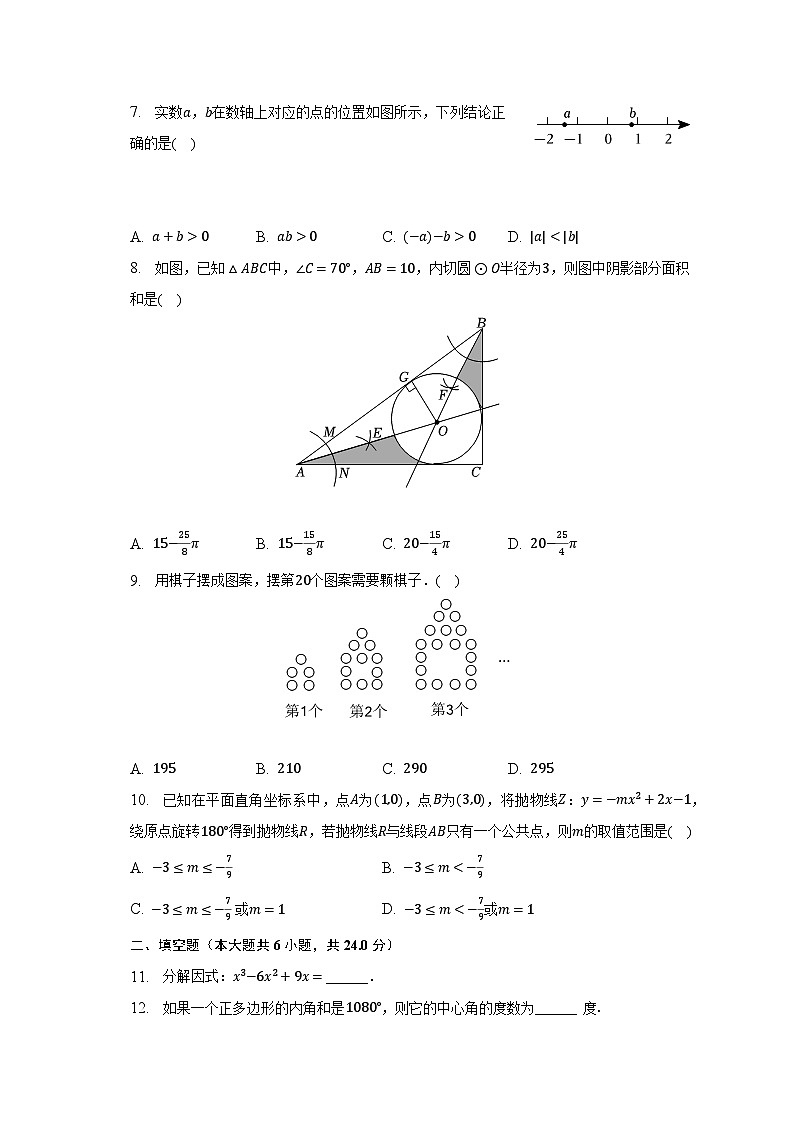
2. 如图所示的几何体的左视图是( )
A.
B.
C.
D.
3. 人的大脑每天能记录大约8600万条信息,把数据“8600万”用科学记数法表示为( )
A. 0.86×104 B. 8.6×103 C. 8.6×107 D. 8.6×108
4. 下列图案中,既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
5. 若方程x2−cx+4=0有两个不相等的实数根.则c的值不可能是( )
A. 10 B. 6 C. 3 D. −5
6. 一个不透明的袋子中装有3个小球,其中2个红球,1个绿球,这些小球除颜色外无其他差别,从袋子中随机摸出两个球,恰好都是红球的概率为( )
A. 16 B. 13 C. 12 D. 23
7. 实数a,b在数轴上对应的点的位置如图所示,下列结论正确的是( )
A. a+b>0 B. ab>0 C. (−a)−b>0 D. |a|<|b|
8. 如图,已知△ABC中,∠C=70°,AB=10,内切圆⊙O半径为3,则图中阴影部分面积和是( )
A. 15−258π B. 15−158π C. 20−154π D. 20−254π
9. 用棋子摆成图案,摆第20个图案需要颗棋子.( )
A. 195 B. 210 C. 290 D. 295
10. 已知在平面直角坐标系中,点A为(1,0),点B为(3,0),将抛物线Z:y=−mx2+2x−1,绕原点旋转180°得到抛物线R,若抛物线R与线段AB只有一个公共点,则m的取值范围是( )
A. −3≤m≤−79 B. −3≤m<−79
C. −3≤m≤−79 或m=1 D. −3≤m<−79或m=1
二、填空题(本大题共6小题,共24.0分)
11. 分解因式:x3−6x2+9x=______.
12. 如果一个正多边形的内角和是1080°,则它的中心角的度数为______ 度.
13. 小华在如图所示的4×4正方形网格纸板上玩飞镖游戏(每次飞镖均落在纸板上,且落在纸板的任何一个点的机会都相等),则飞镖落在阴影区域的概率是______.
14. 设x1、x2是方程x2−x+2m−1=0的两个实数根,若x1⋅x2>0,则m的取值范围是______ .
15. 甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地.如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系式;折线B−C−D−表示轿车离甲地距离y(千米)与x(小时)之间的函数关系,则货车出发______小时与轿车相遇.
16. 如图,现有边长为4的正方形纸片ABCD,点P为AD边上的一点(不与点A点D重合),将正方形纸片沿EF折叠,使点B落在P处,点C落在G处,PG交DC于H,连结BP、BH,下列结论:
①BP=EF;
②当P为AD中点时,△PAE三边之比为3:4:5;
③∠APB=∠BPH;
④△PDH周长等于8.
其中正确的是______ (写出所有正确结论的序号)
三、解答题(本大题共10小题,共86.0分。解答应写出文字说明,证明过程或演算步骤)
17. (本小题8.0分)
计算: 12+(−12)−2−|2−tan60°|+(2022−π)0.
18. (本小题8.0分)
解不等式组,2(x−1)≤x+11−2x+53≤x并写出它的正整数解.
19. (本小题8.0分)
如图,已知▱ABCD中,BE⊥AC于E,DF⊥AC于F.
求证:BF=DE.
20. (本小题80.0分)
某校为调查学生对海洋科普知识的了解情况,从全校学生中随机抽取n名学生进行测试,测试成绩进行整理后分成五组,并绘制成如图的频数分布直方图和扇形统计图.
请根据图中信息解答下列问题:
(1)补全频数分布直方图;
(2)在扇形统计图中,“70~80”这组的百分比m= ;
(3)已知“80~90”这组的数据如下:83,85,87,81,86,84,88,85,86,86,88,89.这组数据的众数是 分;抽取的n名学生测试成绩的中位数是 分;
(4)若成绩达到80分以上(含80分)为优秀,请你估计全校1200名学生对海洋科普知识了解情况为优秀的学生人数.
21. (本小题8.0分)
如图,小文在数学综合实践活动中,利用所学的数学知识测量居民楼的高度AB,在居民楼前方有一斜坡,坡长CD=18m,斜坡CD的坡度i=1: 3.小文在点C处测得楼顶端A的仰角为63°,在D点处测得楼顶端A的仰角为37°(点A,B,C,D在同一平面内).
(结果精确到1m,参考数据:sin63°≈910,cos63°≈920,tan63°≈2,sin37°≈35,cos37°≈45,tan37°≈34, 3≈1.7)
(1)求∠CAD度数;
(2)求居民楼的高度AB.
22. (本小题8.0分)
△ABC中,点O在BC上,以OC为半径的⊙O恰好与AB相切,切点为D,连接CD,且CD⊥AC.
(1)求证:∠BCD=∠A.
(2)设tanA=34,BD=6,求⊙O的半径之长.
23. (本小题8.0分)
某学校为改善办学条件,计划采购A、B两种型号的空调,已知A型空调的单价是B型空调单价的1.5倍,用108000元购买的A型空调数量比用90000元购买的B型空调数量少3台.
(1)求A型空调和B型空调每台各需多少元;
(2)若学校计划采购A、B两种型号空调共30台,且A型空调的台数不少于B型空调的一半,两种型号空调的采购总费用不超过217000元,该校共有哪几种采购方案?
(3)在(2)的条件下,采用哪一种采购方案可使总费用最低,最低费用是多少元?
24. (本小题8.0分)
如图,在平面直角坐标系中,点O为坐标原点,点A的坐标为(3,0),四边形OABC为平行四边形,反比例函数y=kx(x>0)的图象经过点C,与边AB交于点D.若OC=2 2,tan∠AOC=1.
(1)求反比例函数的表达式;
(2)点P(a,0)是一动点,求|PC−PD|最大时a的值;
(3)连接CA,在反比例函数图象上是否存在点M,平面内是否存在点N,
使得四边形CAMN为矩形?若存在,请直接写出点M的横坐标;若不存在,请说明理由.
25. (本小题8.0分)
(1)问题呈现:
如图1,△ABC和△ADE都是等边三角形,连接BD,CE.易知BDCE= ______ .
(2)类比探究
如图2,△ABC和△ADE都是Rt△,∠ABC=∠ADE=90°,且ABBC=ADDE=34.连接BD,CE,求BDCE的值;
(3)拓展提升:
如图3,△ABC是等腰直角三角形,∠ACB=90°,将△ABC绕点A逆时针旋转60°得到△ADE,连接BD,EC,延长EC交BD于点F,设AB=6,求EF的长.
26. (本小题8.0分)
二次函数y=ax2+bx−3的图象交x轴于点A(−1,0),点B(3,0),交y轴于点C,抛物线的顶点为点M.
(1)求二次函数的解析式;
(2)如图1,点P是抛物线上的一点,设点P的横坐标为m(m>3),点Q在对称轴上,且AQ⊥PQ,若AQ=2PQ,请求出m的值;
(3)如图2,将抛物线绕x轴正半轴上一点R旋转180°得到新抛物线C1交x轴于D、E两点,点A的对应点为点E,点B的对应点为点D.若sin∠BME=35,求旋转中心点R的坐标.
答案和解析
1.【答案】B
【解析】解:−32的倒数是−23.
故选:B.
乘积是1的两数互为倒数,由此即可得到答案.
本题考查倒数,关键是掌握倒数的定义.
2.【答案】B
【解析】解:从左边看,可得如图:
.
故选:B.
根据从左边看得到的图形是左视图即可解答.
本题考查了简单组合体的三视图,掌握从左边看得到的图形是左视图为解答本题的关键.
3.【答案】C
【解析】解:将8600万=86000000,
用科学记数法表示为8.6×107.
故选:C.
科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正数;当原数的绝对值<1时,n是负数.
本题考查了科学记数法的表示方法,掌握形式为a×10n的形式,其中1≤|a|<10是关键.
4.【答案】B
【解析】解:A.不是中心对称图形,是轴对称图形,故此选项不合题意;
B.既是轴对称图形,又是中心对称图形,故此选项符合题意;
C.不是中心对称图形,是轴对称图形,故此选项不合题意;
D.是中心对称图形,不是轴对称图形,故此选项不合题意;
故选:B.
根据中心对称图形与轴对称图形的概念,把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,进行判断即可.
本题考查的是中心对称图形与轴对称图形的概念,正确掌握相关定义是解题关键.
5.【答案】C
【解析】解:∵方程x2−cx+4=0有两个不相等的实数根,
∴Δ>0,即(−c)2−4×1×4=c2−16>0,
整理得:(c+4)(c−4)>0,
解得:c>4或c<−4,
则c的值不可能是3.
故选:C.
根据方程有两个不相等的实数根,得到根的判别式大于0,求出c的范围,即可作出判断.
此题考查了根的判别式,熟练掌握根的判别式的意义是解本题的关键.
6.【答案】B
【解析】解:画树状图如下:
总计有6种可能结果,其中我们关注的事件两个都是红球的情况有2种,
∴随机摸出两个球,恰好都是红球的概率为:26=13.
故选:B.
根据随机事件概率大小的求法,找准两点:①符合条件的情况数目;②全部情况的总数,二者的比值就是其发生的概率的大小.
此题考查了概率公式,明确概率的意义是解答问题的关键,用到的知识点为:概率=所求情况数与总情况数之比.
7.【答案】C
【解析】解:根据数轴可知:a<−1、0
故选:C.
根据图中的点的位置即可确定a、b的正负,即可判断.
本题考查数轴与实数对应关系、绝对值、有理数的加减法,乘除法知识,熟记运算法则是解题的关键.
8.【答案】A
【解析】解:∵⊙O是△ABC的内切圆,切点分别为G,D,R,
∴图中阴影部分面积和是△AOB的面积−扇形TOQ的面积,
∵OA、OB分别是∠CAB、∠CBA的角平分线,
∴∠OAB=12∠CAB,∠OBA=12∠CBA,
∵∠ACB=70°,
∴∠CAB+∠CBA=180°−70°=110°,
∴∠OAB+∠OBA=12∠CAB+12∠CBA=55°,
∴∠AOB=180−(∠OAB+∠OBA)=125°,
∴S阴影=S△AOB−S扇形=12×10×3−125360×π×32=15−258π,
故选:A.
根据内切圆的性质可得图中阴影部分面积和是△AOB的面积−扇形TOQ的面积,进而即可求解.
本题考查了三角形的内切圆与内心,扇形面积的计算,解决本题的关键是掌握三角形的内切圆与内心.
9.【答案】C
【解析】解:∵第1个图形中的棋子的个数为:5=1+2×4−4,
第2个图形中的棋子的个数为:11=1+2+3×4−4,
第3个图形中的棋子的个数为:18=1+2+3+4×4−4,
…,
∴第n个图形中的棋子的个数为:1+2+3+…+n+4(n+1)−4=n(n+1)2+4n,
∴第20个图形中的棋子的个数为:20×212+4×20=290.
故选:C.
第1个图形中的棋子的个数为:5=1+2×4−4,第2个图形中的棋子的个数为:11=1+2+3×4−4,第3个图形中的棋子的个数为:18=1+2+3+4×4−4,…,据此可求得第n个图形中的棋子的个数,从而可求解.
本题主要考查图形的变化规律,解答的关键是由所给的图形总结出第n个图形中的棋子的个数.
10.【答案】A
【解析】解:将抛物线Z:y=−mx2+2x−1,绕原点旋转180°得到抛物线R:−y=−m(−x)2+2(−x)−1,即y=mx2+2x+1,
当抛物线R经过点A时,则m+2+1=0,解得m=−3;
当抛物线R经过点B时,则9m+6+1=0,解得m=−79,
当抛物线y=mx2+2x+1与x轴有一个交点时,则Δ=0,
∴4−4m=0,解得m=1,此时y=x2+2x+1,与x轴的交点为(−1,0),不合题意,
∴若抛物线R与线段AB只有一个公共点,则m的取值范围是−3≤m≤−79.
故选:A.
根据关于原点对称的点的坐标特征得到抛物线R:y=mx2+2x+1,把点A(1,0),点B(3,0)分别代入求得m的值,即可求得m的取值范围.
本题考查了二次函数图象与系数的关系,二次函数图象上点的坐标特征,二次函数图象与几何变换,求得绕原点旋转180°后抛物线的解析式是解题的关键.
11.【答案】x(x−3)2
【解析】先提取公因式x,再对余下的多项式利用完全平方公式继续分解.
本题考查因式分解的提公因式法和公式法的综合运用,熟练掌握因式分解的基本方法是解题的关键.
解:x3−6x2+9x,
=x(x2−6x+9),
=x(x−3)2.
故答案为:x(x−3)2.
12.【答案】45
【解析】解:设此多边形为n边形,
根据题意得:180°(n−2)=1080°,
解得:n=8,
∴这个正多边形的每一个外角等于:360°÷8=45°.
故答案为:45.
首先设此多边形为n边形,根据题意得:180°(n−2)=1080°,即可求得n=8,再由多边形的外角和等于360°,即可求得答案.
本题考查了多边形的内角和与外角和的知识.关键是掌握多边形内角和定理:(n−2)⋅180°,外角和等于360°.
13.【答案】516
【解析】解:阴影部分的面积是:16−4−1×32×2−2×42=5,
则飞镖落在阴影区域的概率是516;
故答案为:516.
用正方形的总面积减去空白部分的面积,求出阴影部分的面积,再根据概率公式即可得出答案.
此题主要考查了几何概率,正确掌握概率公式是解题关键.
14.【答案】12
解得m≤58,
∵x1⋅x2=2m−1
∴2m−1>0,
解得m>12,
∴m的取值范围为12
本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=−ca,x1x2=ca.也考查了根与系数的关系.
15.【答案】3.9
【解析】解:设OA段对应的函数解析式为y=kx,
将(5,300)代入,得:5k=300,
解得k=60,
即OA段对应的函数解析式为y=60x,
设CD段对应的函数解析式为y=ax+b,
2.5a+b=804.5a+b=300,
解得a=110b=−195,
即CD段对应的函数解析式为y=110x−195,
令110x−195=60x,得x=3.9,
即货车出发3.9小时与轿车相遇,
故答案为:3.9.
根据函数图象中的数据,可以分别求得OA段和CD对应的函数解析式,然后令它们相等,求得x的值,即可得到货车出发几小时与轿车相遇.
本题考查一次函数的应用,解答本题的关键是明确题意,利用数形结合的思想解答.
16.【答案】①②③④
【解析】解:如图,过点F作FM⊥AB于点M,
∵四边形ABCD为正方形,
∴∠A=∠ABC=90°,AB=BC,
∵FM⊥AB,
∴四边形MBCF为矩形,
∴MF=BC=AB,∠FME=90°,
由折叠可知,EF⊥BP,
∴∠PBE+∠BEF=90°,
∵∠PBE+∠APB=90°,
∴∠BEF=∠APB,即∠MEF=∠APB,
在△ABP和△MFE中,
∠APB=∠MEF∠BAP=∠FMEAB=MF,
∴△ABP≌△MFE(AAS),
∴BP=EF,故①正确;
由折叠可知,BP=PE,
设BP=PE=x,则AE=4−x,
∵P为AD中点,
∴AP=2,
在Rt△PAE中,AP2+AE2=PE2,
∴22+(4−x)2=x2,
解得:x=52,
∴AE=4−x=32,PE=52,
∴AE:AP:PE=32:2:52=3:4:5,
即△PAE三边之比为3:4:5,故②正确;
由折叠可知,BE=PE,∠EBC=∠EPC=90°,
∴∠PBE=∠BPE,∠BPE+∠BPH=90°,
∵∠PBE+∠APB=90°,
∴∠APB=∠BPH,故③正确;
如图,过点B作BN⊥PH于点N,
∴∠BAP=∠BNP=90°,
在△ABP和△NBP中,
∠BAP=∠BNP∠APB=∠NPBPB=PB,
∴△ABP≌△NBP(AAS),
∴AB=BN,AP=PN,
∴BC=BN,
在Rt△BNH和Rt△BCH中,
BN=BCBH=BH,
∴Rt△BNH≌Rt△BCH(HL),
∴NH=CH,
∴C△PDH=PD+PN+NH+DH=PD+AP+CH+DH=2AD=8,故④正确.
综上,正确的结论有①②③④.
故答案为:①②③④.
过点F作FM⊥AB于点M,易得MF=BC=AB,由折叠可知EF⊥BP,于是利用同角的余角相等可得∠MEF=∠APB,以此可通过AAS证明△ABP≌△MFE,即可判断①;由折叠可知BP=PE,设BP=PE=x,则AE=4−x,在Rt△PAE中,利用勾股定理建立方程,求解即可判断②;利用等角的余角相等即可判断③;过点B作BN⊥PH于点N,易通过AAS证明△ABP≌△NBP,得到AB=BN,AP=PN,以此再通过HL证明Rt△BNH≌Rt△BCH,得到NH=CH,则C△PDH=2AD,即可判断④.
本题主要考查正方形的性质、折叠的性质、全等三角形的判定与性质、勾股定理,正确作出辅助线,构建合适的全等三角形解决问题是解题关键.
17.【答案】解:原式=2 3+4−(2− 3)+1
=2 3+4−2+ 3+1
=3 3+3.
【解析】利用二次根式的性质,负整数指数幂的意义,绝对值的意义和零指数幂的意义化简运算即可.
本题主要考查了实数的运算,二次根式的性质,负整数指数幂的意义,绝对值的意义和零指数幂的意义,熟练掌握上述法则与性质是解题的关键.
18.【答案】解:2(x−1)≤x+1①1−2x+53≤x②,
解不等式①,得x≤3,
解不等式②,得x≥−25,
所以不等式组的解集是−25≤x≤3,
所以不等式组的正整数解是1,2,3.
【解析】先根据不等式的性质求出不等式的解集,再根据求不等式组解集的规律求出不等式组的解集,最后求出不等式组的正整数解即可.
本题考查了解一元一次不等式组和一元一次不等式组的整数解,能根据求不等式组解集的规律求出不等式组的解集是解此题的关键.
19.【答案】证明:∵四边形ABCD是平行四边形,
∴AB//CD,AB=CD,
∴∠BAE=∠DCF,
∵BE⊥AC于E,DF⊥AC于F,
∴∠BEA=∠DFC,
在△ABE和△CDF中,
∠BAE=∠CDF∠BEA=∠DFCAB=CD,
∴△ABE≌△DFC(AAS),
∴BE=DF,
∵∠BEA=∠DFC,
∴∠BEF=∠DFE,
∴BE//DF,
∴四边形BEDF是平行四边形,
∴BF=DE.
【解析】根据AAS证明△ABE≌△DFC得出BE=DF,再证明四边形BEDF是平行四边形即可得出结论.
本题考查了全等三角形的判定与性质,平行四边形的判定性质,证明△ABE≌△DFC是解题的关键.
20.【答案】20% 86 84.5
【解析】解:(1)8÷16%=50(人),50−4−8−10−12=16(人),
补全频数分布直方图如下:
(2)m=1050×100%=20%;
故答案为:20%;
(3)将“80~90”这组数据进行排序:
81,83,84,85,85,86,86,86,87,88,88,89,出现次数最多的为86,
∴众数为86分,
故答案为:86;
∵“50~80”分的人数已有22人,
∴第25和26名的成绩分别是是84分,85分,
∴中位数是84+852=84.5分;
故答案为:84.5;
(4)1200×12+1650=672(人).
∴优秀人数是672人.
(1)先求出样本容量,再用样本容量减去已知各部分的频数,即可求出“90~100”这组的频数,从而补全频数分布直方图;
(2)用“70~80”这组的频数除以样本容量即可;
(3)根据众数和中位数的定义求解即可;
(4)用1200乘以80分以上人数所占的比例即可.
本题主要考查了频数分布直方图、扇形统计图的综合和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.也考查了利用样本估计总体,求数据的众数与中位数.
21.【答案】解:(1)过点D作DE⊥BC,垂足为E,过点D作DF⊥AB,垂足为F,
由题意得:DF//BE,
∵斜坡CD的坡度i=1: 3,
∴DECE=1 3= 33,
在Rt△DCE中,tan∠DCE=DECE= 33,
∴∠DCE=30°,
∵∠ACB=63°,
∴∠ACD=180°−∠ACB−∠DCE=87°,
∵DF//BE,
∴∠FDC=∠DCE=30°,
∵∠ADF=37°,
∴∠ADC=∠ADF+∠FDC=67°,
∴∠CAD=180°−∠ACD−∠ADC=26°,
∴∠CAD度数为26°;
(2)由题意得:DF=BE,BF=DE,
在Rt△DCE中,CD=18m,∠DCE=30°,
∴DE=12CD=9(m),CE= 3DE=9 3(m),
∴BF=DE=9 3m,
设BC=x m,
∴DF=BE=BC+CE=(x+9 3)m,
在Rt△ABC中,∠ACB=63°,
∴AB=BC⋅tan63°≈2x(m),
在Rt△ADF中,∠ADF=37°,
∴AF=DF⋅tan37°≈34(x+9 3)m,
∵AB−AF=BF,
∴2x−34(x+9 3)=9,
解得:x≈16.38,
∴AB=2x≈33(m),
∴居民楼的高度AB约为33m.
【解析】(1)过点D作DE⊥BC,垂足为E,过点D作DF⊥AB,垂足为F,根据题意可得:DF//BE,根据已知可得:在Rt△DCE中,tan∠DCE= 33,从而可得∠DCE=30°,然后利用平角定义求出∠ACD=87°,再利用平行线的性质可得∠FDC=∠DCE=30°,从而可得∠ADC=67°,最后利用三角形内角和定理进行计算,即可解答;
(2)根据题意可得:DF=BE,BF=DE,在Rt△DCE中,利用含30度角的直角三角形的性质求出DE,CE的长,然后设BC=xm,则DF=BE=(x+9 3)m,在Rt△ABC中,利用锐角三角函数的定义求出AB的长,再在Rt△ADF中,利用锐角三角函数的定义求出AF的长,最后根据AB−AF=BF,列出关于x的方程,进行计算即可解答.
本题考查了解直角三角形的应用−仰角俯角问题,坡度坡角问题,根据题目的一已知条件并结合图形添加适当的辅助线是解题的关键.
22.【答案】(1)证明:连接OD,如图,
∵以OC为半径的⊙O恰好与AB相切,
∴OD⊥AB,
∴∠ODA=90°,
∴∠ODC+∠ADC=90°,
∵OC=OD,
∴∠ODC=∠OCD,
∴∠BCD+∠ADC=90°.
∵CD⊥AC,
∴∠A+∠ADC=90°,
∴∠BCD=∠A;
(2)解:设⊙O的半径为r,则OD=OC=r,
∵tanA=34,tanA=CDAC,
∴CDAC=34.
∵∠BCD=∠A,∠B=∠B,
∴△BCD∽△BAC,
∴BDBC=BCAB=CDAC=34,
∴6BC=34,
∴6BO+r=34,
∴BO=8−r.
在Rt△OBD中,
∵OD2+BD2=BO2,
∴r2+62=(8−r)2,
解得:r=74.
∴⊙O的半径之长为74.
【解析】(1)连接OD,利用切线的性质定理,同圆的半径相等,等腰三角形的性质定理,直角三角形的性质和等角的余角相等解答即可;
(2)设⊙O的半径为r,则OD=OC=r,判定△BCD∽△BAC,利用相似三角形的性质定理得出比例式得到BO=8−r,在Rt△OBD中,利用勾股定理列出关于r的方程,解方程即可得出结论.
本题主要考查了圆的有关性质,圆的切线的性质定理,直角三角形的性质,直角三角形的边角关系定理,相似三角形的判定与性质,连接经过切点的半径是解决此类问题常添加的辅助线.
23.【答案】解:(1)设B型空调每台需x元,则A型空调每台需1.5x元,
根据题意得:1080001.5x=90000x−3,
解得:x=6000,
经检验,x=6000是原方程的解,
∴1.5x=1.5×6000=9000,
∴A型空调每台需9000元,B型空调每台需6000元;
(2)设采购m台A型空调,则采购(30−m)台B型空调,
∵A型空调的台数不少于B型空调的一半,两种型号空调的采购总费用不超过217000元,
∴m≥12(30−m)9000m+6000(30−m)≤217000,
解得:10≤m≤1213,
∵m为整数,
∴m可取10,11,12,
∴学校共有3种采购方案:采购10台A型空调,采购20台B型空调或采购11台A型空调,采购19台B型空调或采购12台A型空调,采购18台B型空调;
(3)设总费用为w,
根据题意得:w=9000m+6000(30−m)=3000m+180000,
∵3000>0,
∴w随m的增大而增大,
∴m=10时,w取最小值,最小值为3000×10+180000=210000(元),
∴采购10台A型空调,采购20台B型空调可使总费用最低,最低费用是210000元.
【解析】(1)设B型空调每台需x元,可得得:1080001.5x=90000x−3,解方程并检验可得答案;
(2)根据A型空调的台数不少于B型空调的一半,两种型号空调的采购总费用不超过217000元,列不等式组,由m为整数可得答案;
(3)设总费用为w,可得:w=9000m+6000(30−m)=3000m+180000,根据一次函数性质可得答案.
本题考查一次函数,分式方程的应用,涉及一元一次不等式组的应用,解题的关键是读懂题意,列出方程和函数关系式.
24.【答案】解:(1)如图,过点C作CE⊥x轴于E,
∴∠CEO=90°,
∵tan∠AOC=1
∴∠COA=45°,
∴∠OCE=45°,
∵OC=2 2,
∴OE=CE=2,
∴C(2,2),
∵点C在反比例函数图象上,
∴k=2×2=4,
∴反比例函数解析式为y=4x;
(2)∵点C(2,2),点O(0,0),
∴OC解析式为:y=x,
∵四边形OABC是平行四边形,
∴BC=OA=3,BC//OA,AB//OC,
∴点B(5,2),
∴设AB解析式为:y=x+b,
∴2=5+b,
∴b=−3,
∴AB解析式为:y=x−3,
联立方程组可得:y=4xy=x−3,
∴x=4y=1或x=−1y=−4(舍去),
∴点D(4,1);
在△PCD中,|PC−PD|
∴2m+n=24m+n=1,解得m=−12n=3,
∴直线CD的解析式为:y=−12x+3,
令y=0,即−12x+3=0,得x=6,
∴|PC−PD|最大时a的值为6.
(3)存在,理由如下:
若四边形CAMN为矩形,则△CAM是直角三角形,
则①当点A为直角顶点时,如图2,过点A作AC的垂线与y=4x交于点M,分别过点C,M作x轴的垂线,垂足分别为点F,G,
由“一线三等角”模型可得△AFC∽△MGA,
则AF:MG=CF:AG,
∵C(2,2),A(3,0),
∴OF=CF=2,AF=1,
∴1:MG=2:AG,即MG:AG=1:2,
设MG=t,则AG=2t,
∴M(2t+3,t),
∵点M在反比例函数y=4x的图象上,
则t(2t+3)=4,
解得t=−3+ 414,(负值舍去),
∴M(3+ 412,−3+ 414);
②当点C为直角顶点时,这种情况不成立;
综上,点M的坐标为(3+ 412,−3+ 414).
【解析】(1)先确定出OE=CE=2,即可得出点C坐标,最后用待定系数法即可得出结论;
(2)先求出OC解析式,由平行四边形的性质可得BC=OA=3,BC//OA,AB//OC,利用待定系数法可求AB解析式,求出点D的坐标,再根据三角形关系可得出当点P,C,D三点共线时,|PC−PD|最大,求出直线CD的解析式,令y=0即可求解;
(3)若四边形CAMN为矩形,则△CAM是直角三角形且AC为一条直角边,根据直角顶点需要分两种情况,画出图形分别求解即可.
本题考查了反比例函数综合问题,涉及矩形的判定与性质,相似三角形的性质与判定.第一问的关键是求出点C的坐标,第二问的关键是知道当点P,C,D三点共线时,|PC−PD|取得最大值,第三问的关键是利用矩形的内角是直角进行分类讨论,利用相似三角形的性质建立等式.
25.【答案】1
【解析】解:(1)∵△ABC和△ADE都是等边三角形,
∴AD=AE,AB=AC,∠DAE=∠BAC=60°,
∴∠DAE−∠BAE=∠BAC−∠BAE,
∴∠BAD=∠CAE,
∴△BAD≌△CAE(SAS),
∴BD=CE,
∴BDCE=1,
故答案为:1;
(2)∵ABBC=ADDE=34,∠ABC=∠ADE=90°,
∴△ABC∽△ADE,
∴∠BAC=∠DAE,ABAC=ADAE=35;
∴∠CAE=∠BAD,
∴△CAE∽△BAD,
∴BDCE=ADAE=35;
(3)如图,过点D作DH//BC,交EF的延长线于H,过点D作DN⊥EF于N,
∵△ABC是等腰直角三角形,∠ACB=90°,AB=6,
∴AC=BC=3 2,
∵将△ABC绕点A逆时针旋转60°得到△ADE,
∴AB=AD,AC=AE,∠BAD=∠CAE=60°,BC=DE,∠ACB=∠AED=90°,
∴△ABD和△ACE都是等边三角形,
∴AB=BD=6,∠ACE=∠AEC=60°,
∴∠BCF=∠DEF=30°,
∵DH//BC,
∴∠BCF=∠H=30°=∠DEF,
∴DH=DE=BC=3 2,
又∵∠BCF=∠DEF,∠BFC=∠DFH,
∴△BCF≌△DHF(AAS),
∴BF=DF=12BD=3,
∵DN⊥EF,∠DEF=30°,
∴DN=12DE=3 22,NE= 3DN=3 62,
∵FN= FD2−ND2= 9−184=3 22,
∴EF=FN+EN=3 62+3 22=3 6+3 22.
(1)证明△BAD≌△CAE,从而得出结论;
(2)先证明△ABC∽△ADE,再证得△CAE∽△BAD,进而得出结果;
(3)由“AAS”可证△BCF≌△DHF,可得BF=DF=12BD=3,由直角三角形的性质可求解.
本题是相似形综合题,考查了等边三角形的性质,等腰直角三角形的性质,全等三角形的判定和性质,相似三角形的判定和性质,添加恰当辅助线构造全等三角形是解题的关键.
26.【答案】解:(1)将A(−1,0),点B(3,0),代入函数解析式得:a−b−3=09a+3b−3=0,
解得:a=1b=−2,
∴这个二次函数的表达式是y=x2−2x−3;
(2)过点Q作x轴的平行线交过点P与y轴的平行线与点N,交过点A与y轴的平行线于点M,
∵∠NQP+∠MQA=90°,∠MQA+∠QAM=90°,
∴∠NQP=∠QAM,
∵∠AMQ=∠QNP=90°,
∴△AMQ∽△QNP,
∴AMQN=MQNP=AQQP=2,
设点Q的坐标为(1,t),点P的坐标为(m,m2−2m−3),
则AM=t,QN=m−1,MQ=2,NP=t−m2+2m+3,
即tm−1=2t−m2+2m+3=2,
解得m=0(舍去)或4,
故m=4;
(3)过点E作EH⊥MB交MB的延长线于点H,
由抛物线的表达式知,点M(1,−4),BM=2 5,
则tan∠OBM=OMOB=2=tan∠HBE,
∵sin∠BME=35,故tan∠BME=34,
故设BH=x,则HE=2x,
在Rt△HEM中,tan∠BME=34,MB=2 5,
则tan∠BME=34=HEMH=2xx+2 5,解得x=6 5,
在Rt△BHE中,BE= BH2+HE2= 5x=6,
故点E的坐标为(9,0),
由旋转的定义知,点R是点A、E的中点,
则xR=12(9−1)=4,
故点R的坐标为(4,0).
【解析】(1)用待定系数法即可求解;
(2)证明△AMQ∽△QNP,则AMQN=MQNP=AQQP=2,即可求解;
(3)在Rt△HEM中,tan∠BME=34,MB=2 5,则tan∠BME=34=HEMH=2xx+2 5,解得x=6 5,在Rt△BHE中,BE= BH2+HE2= 5x=6,故点E的坐标为(9,0),进而求解.
本题是二次函数综合题,主要考查了一次函数的性质、直角三角形的性质、图形的旋转、解直角三角形等,综合性强,难度适中.
2023年山东省济南市天桥区中考数学三模试卷(含解析): 这是一份2023年山东省济南市天桥区中考数学三模试卷(含解析),共28页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
2023年山东省济南市莱芜区中考数学三模试卷(含解析): 这是一份2023年山东省济南市莱芜区中考数学三模试卷(含解析),共26页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023年山东省济南市市中区育英中学中考数学三模试卷(含解析): 这是一份2023年山东省济南市市中区育英中学中考数学三模试卷(含解析),共27页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。












