适用于新教材2024版高考数学一轮总复习第十一章计数原理概率随机变量及其分布课时规范练51排列与组合北师大版

课时规范练51

基础巩固组

1.(2022·江苏南京三模)为庆祝中国共青团成立100周年,某校计划举行庆祝活动,共有4个节目,要求A节目不排在第一个,则节目安排的方法数为(　　)

A.9 B.18 C.24 D.27

答案:B

解析:由题意,先从后面3个节目中选择一个安排A节目,然后其他3个节目任意排在剩下的3个位置,共有=18种方法.

2.(2023·陕西交大附中模拟)将4个9和2个6随机排成一行,则2个6不相邻共有(　　)种不同的排法.

A.240 B.120 C.20 D.10

答案:D

解析:若2个6不相邻,只需将2个6插入4个9所形成5个空的2个空中,故不同的排法种数为=10.

3.(2022·广东汕头三模)2022年北京冬季奥运会期间,从3名男志愿者和2名女志愿者中选4名去支援“冰壶”“花样滑冰”“短道速滑”三项比赛志愿者工作,其中冰壶项目需要一男一女两名,花样滑冰和短道速滑各需要一名,男女不限.则不同的支援方法的种数是(　　)

A.36 B.24 C.18 D.42

答案:A

解析:第一步从3名男志愿者和2名女志愿者各选一名志愿者去支援冰壶项目,选法共有=6种;第二步从剩余的3人中选一人去支援花样滑冰,选法共有=3种;第三步从剩余的2人中选一人去支援短道速滑,选法共有=2种.依据分步乘法计数原理可知,不同的支援方法的种数是6×3×2=36.

4.(2022·河北秦皇岛二模)“学习强国”学习平台是立足全体党员、面向全社会的优质平台,现日益成为人们了解国家动态,紧跟时代脉搏的热门APP.该款软件主要设有“阅读文章”“视听学习”两个学习版块和“每日答题”“每周答题”“专项答题”“挑战答题”四个答题版块.某人在学习过程中,将六大版块各完成一次,则“挑战答题”版块与其他三个答题版块在完成顺序上均不相邻的学习方法种数为(　　)

A.144 B.72 C.96 D.36

答案:A

解析:当“挑战答题”版块在首或尾时,则与“挑战答题”版块相邻的只能是“阅读文章”或“视听学习”版块,其他任意排,共有=96种不同的排法;当“挑战答题”版块不在首尾时,则与“挑战答题”版块相邻的只能是“阅读文章”和“视听学习”版块,其他任意排,共有=48种不同的排法.

所以“挑战答题”版块与其他三个答题版块在完成顺序上均不相邻的学习方法种数为96+48=144.

5.(2022·山东淄博三模)若=6(m∈N*,m≥4),则m=　　　　　. 

答案:7

解析:因为=6(m∈N*,m≥4),所以m(m-1)(m-2)=6×,即6(m-3)=4!,解得m=7.

6.(2022·湖南邵阳、郴州二模)一次考试后,学校准备表彰在该次考试中表现优异的10位同学,其中有2位是高三(1)班的同学,现要选4人去“表彰会”上作报告,若高三(1)班的2人同时参加,则2人作报告的顺序不能相邻,则要求高三(1)班至少有1人参加的作报告的方案共有　　　　　种(用数字作答). 

答案:3 024

解析:若高三(1)班只有1人参加,则有=2688种不同的方案;若高三(1)班2人都参加,则有=336种不同方案,故共有3024种不同的方案.

综合提升组

7.(多选)(2023·海南华侨中学高三检测)身高各不相同的六位同学A,B,C,D,E,F站成一排照相,则说法正确的是(　　)

A.A,C,D三位同学从左到右按照由高到矮的顺序站,共有种站法

B.A与C同学不相邻,共有种站法

C.A,C,D三位同学必须站在一起,且A只能在C与D的中间,共有种站法

D.A不在排头,B不在排尾,共有-2种站法

答案:ABD

解析:A:6个人全排列有种方法,A,C,D全排列有种方法,所以A,C,D从左到右按高到矮的排列有种方法,故A正确;

B:先排列除A与C外的4个人,有种方法,4个人排列共有5个空,利用插空法将A和C插入5个空,有种方法,所以共有种方法,故B正确;

C:A,C,D必须排在一起且A在C,D中间的排法有2种,将这3人捆绑在一起,与其余3人全排列,有种方法,所以共有2种方法,故C错误;

D:6个人全排列有种方法,当A在排头时,有种方法,当B在排尾时,有种方法,当A在排头且B在排尾时,有种方法,所以A不在排头,B不在排尾的情况共有-2种,故D正确.故选ABD.

8.(2023·江苏无锡模拟)甲、乙、丙、丁、戊共5名同学进行劳动技术比赛,决出第1名到第5名的名次,已知甲和乙都没有得到冠军,并且乙不是第5名,则这5个人的名次排列情况共有　　　　　种. 

答案:54

解析:因为甲和乙都没有得到冠军,并且乙不是第5名,当甲是第5名时,则乙可以为第2,3,4名,有3种情况,剩下的3人全排列有=6种,此时,由分步乘法计数原理得共有3×6=18种情况;

当甲不是第5名时,则甲乙排在第2,3,4名,有=6种情况,剩下的3人全排列有=6种,此时,由分步乘法计数原理得共有6×6=36种情况.

所以这5个人的名次排列情况共有18+36=54种情况.

9.有2男2女共4名学生被分派去A,B,C三个公司实习,每个公司至少1人,且A公司只收女生,则不同的分派方法数为　　　　　. 

答案:14

解析:由题意,第一类,A公司收1个女生,有=2种分派方案,则B,C公司分派人数可以为1,2或者2,1共2种分派方案,共=6种,所以一共有2×6=12种分派方案,第二类,A公司收2个女生,只有1种分派方案,则B,C公司的分派人数只能是1,1,则有=2种分派方案,根据分类加法计数原理共有12+2=14种.

创新应用组

10.(2023·湖北高三开学考试)如图,某城市的街区由12个全等的矩形组成(实线表示马路),CD段马路由于正在维修,暂时不通,则从A到B的最短路径有(　　)

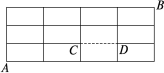
A.23条 B.24条 C.25条 D.26条

答案:D

解析:先假设CD是实线,则从A到B,向上3次,向右4次,最短路径有=35条,其中经过CD的路径,即先从A到C,然后C到D,最后D到B的最短路径有3×3=9条,所以,当CD不通时,最短路径有35-9=26条.

11.(2023·广东珠海模拟)3名女生和4名男生随机站成一排,则每名女生旁边都有男生的概率为　. 

答案:

解析:依题意所有可能情况总数为,若女生都不相邻,首先将4个男生全排列,再将3个女生插入所形成的5个空中的3个空,则有种排法;若有两个女生相邻,首先从3个女生中选出2个并排列作为一个整体A,将4个男生全排列,再将整体A插入中间3个空中的1个,再将另一个女生插入4个空中的1个空,则有种排法,故每名女生旁边都有男生的概率P=.