江苏省泰州市姜堰区四校联考2022-2023学年八年级下学期5月月考数学试卷

这是一份江苏省泰州市姜堰区四校联考2022-2023学年八年级下学期5月月考数学试卷，共17页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

八年级数学月考
一、选择题（本大题共8小题，每小题3分，共24分．在每小题给出的四个选项中，有且只有一项是符合题目要求的，请将正确选项的字母代号填涂在答题卡相应位置上）
1、下列平面直角坐标系内的曲线中，既是中心对称图形，也是轴对称图形的是（　　）
A． 三叶玫瑰线 B． 四叶玫瑰线
C． 心形线 D． 笛卡尔叶形线
2、将分式中的m、n同时扩大为原来的3倍，分式的值将（    ）
A．扩大3倍 B．不变 C．缩小3倍 D．缩小9倍
3、已知反比例函数，则下列描述正确的是（    ）
A．图象位于第一、三象限 B．y随x的增大而增大
C．图象不可能与坐标轴相交 D．图象必经过点
4、为了解某校七年级1000名学生学习中国海军史的情况，学校组织了中国海军史知识测试，并从中随机抽取了200名学生的成绩进行统计分析，下列说法正确的是（　　）
A．1000名学生是总体
B．200名是样本容量
C． 被抽取的200名学生是总体的一个样本
D． 该校七年级每名学生的中国海军史知识测试的成绩是个体
5、某市为“加快推进污水管网建设，着力提升居民生活品质”，需要铺设一段全长为米的污水排放管道，为了尽量减少施工对城市交通所造成的影响，实际施工时每天的工效比原计划增加，结果提前天完成这一任务，设原计划每天铺设x米管道，则根据题意，下列方程中正确的是（    ）
A． B．
C． D．
6、如图，四边形是矩形，点A在x轴正半轴，点C在y轴正半轴，对角线，交于点D．双曲线经过点D与边，分别交于点E，点F，连接，，若四边形的面积为5，则k的值为（    ）

A．5 B． C． D．
二、填空题（本大题共10小题，每题3分，共30分．不需写出解答过程，请把答案直接填写在答题卡相应位置上）
7、 妈妈做菜时，为了了解菜品的咸淡是否合适，取了一点品尝．妈妈的这种做法属于 _____（从“普查”和“抽样调查”中选一）．
8、 当分式有意义，则x的取值范围是 ．
9、 分式，的最简公分母是_____________
10、 将50个数据分成5组列出频数分布表，其中第一组的频数为6，第二组与第五组的频数和为18，第三组的频率为0.2，则第四组的频率为 ．
11、已知关于x的方程的解是正数，则m的取值范围为______．
12、如图，在菱形中，对角线相交于点O，，E是线段上一点，且，则的度数是______．

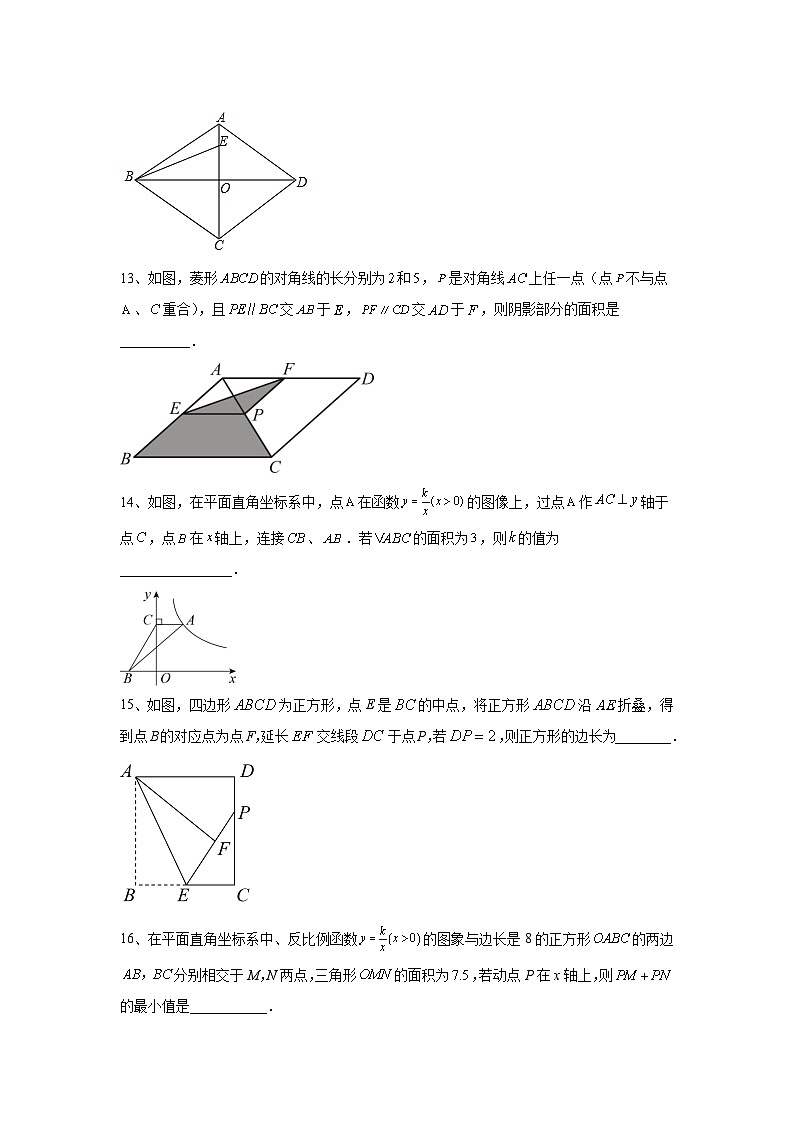
13、如图，菱形的对角线的长分别为和，是对角线上任一点（点不与点、重合），且交于，交于，则阴影部分的面积是__________．

14、如图，在平面直角坐标系中，点在函数的图像上，过点作轴于点，点在轴上，连接、．若的面积为，则的值为________________．

15、如图，四边形为正方形，点E是的中点，将正方形沿折叠，得到点B的对应点为点F，延长交线段于点P，若，则正方形的边长为________．

16、在平面直角坐标系中、反比例函数的图象与边长是8的正方形的两边分别相交于M，N两点，三角形的面积为，若动点P在x轴上，则的最小值是___________．

三、解答题（本大题共10题，共102分．请在答题卡指定区域内作答，解答时应写出必要的文字说明、证明过程或演算步骤）
17（8分）、计算：
（1）；（2）（1）．


18、（8分）解方程：
（1）；（2）．


19、（8分）先化简，再求值：，其中2≥x≥﹣2，且x为整数，请你选一个合适的x值代入求值．


20.（10分）已知：如图，四边形是平行四边形．
（1）用尺规作图，作的垂直平分线，分别交边、于点E、F；
（2）求证：四边形是菱形．



21、（10分）如图，平行四边形的对角线、相交于点，，分别是，的中点．求证：
(1)；
(2)．





22、（10分）已知一次函数y＝kx+b与反比例函数y的图像交于A（﹣3，2）、B（1，n）两点．
(1)求一次函数和反比例函数的表达式；
(2)求△AOB的面积；
(3)结合图像直接写出不等式kx+b的解集．





23、（10分）如图，中，已知，于，，，把、分别以、为对称轴翻折变换，点的对称点为，，延长、相交于点．
（1）求证：四边形是正方形；
（2）求的长．





24．（12分）[定义]平面直角坐标系内的矩形若满足以下两个条件：①各边平行于坐标轴；②有两个顶点在同一反比例函数图象上，我们把这个矩形称为该反比例函数的“伴随矩形”．
例如，图1中，矩形ABCD的边AD∥BC∥x轴，AB∥CD∥y轴，且顶点A、C在反比例函数y＝（k≠0）的图象上，则矩形ABCD是反比例函数y＝的“伴随矩形”．
[解决问题]
（1）已知，矩形ABCD中，点A、C的坐标分别为：①A（﹣3，8），C（6，﹣4）；②A（1，2），C（2，3）；③A（3，4），C（2，6），其中可能是某反比例函数的“伴随矩形”的是 　 　；（填序号）
（2）如图1，已知点B（2，）是反比例函数y＝的“伴随矩形”ABCD的顶点，求直线BD的函数解析式；
（3）若反比例函数的“伴随矩形”ABCD如图2所示，试说明有一条对角线所在的直线一定经过原点．












25．（12分）阅读理解
材料1：为了研究分式与分母x的变化关系，小明制作了表格，并得到如下数据：
x
…
﹣4
﹣3
﹣2
﹣1
0
1
2
3
4
…

…
﹣0.25
﹣0.33…
﹣0.5
﹣1
无意义
1
0.5
0.33…
0.25
…
从表格数据观察，当x＞0时，随着x的增大，的值随之减小，并无限接近0；当x＜0时，随着x的增大，的值也随之减小．
材料2：对于一个分子、分母都是多项式的分式，当分母的次数高于分子的次数时，我们把这个分式叫做真分式．当分母的次数不高于分子的次数时，我们把这个分式叫做假分式．有时候，需要把一个假分式化成整式和真分式的代数和，像这种恒等变形，称为将分式化为部分分式．如：．
根据上述材料完成下列问题：
（1）当x＞0时，随着x的增大，1的值 　 　（增大或减小）；
当x＜0时，随着x的增大，的值 （增大或减小）；
（2）当x＞1时，随着x的增大，的值无限接近一个数，请求出这个数；
（3）当0≤x≤2时，求代数式值的范围．




26．（14分）△ABC中，∠BAC＝90°，AB＝AC，点D为直线BC上一动点（点D不与B，C重合），以AD为边在AD右侧作正方形ADEF，连接CF．

（1）观察猜想：如图1，当点D在线段BC上时，
①BC与CF的位置关系为： ．
②BC，CD，CF之间的数量关系为 ；（将结论直接写在横线上）
（2）数学思考：如图2，当点D在线段CB的延长线上时，（1）中的结论①，②是否仍然成立？若成立，请给予证明；若不成立，请你写出正确结论再给予证明．
（3）拓展延伸如图3，当点D在线段BC的延长线上时，延长BA交CF于点G，连接GE．若已知BC＝4，CD＝1，请直接写出GE的长．




















参考答案
1、 B 2、C 3、C 4、D 5、C 6、D
7、 抽样调查
8、 x≠0
9、 6x2y
10、 0.32
11、 M≥-4且m≠-3
12、 25
13、 2.5
14、 6
15、 6
16、
17、解：（1）原式1；
（2）原式＝（）•
•
．
18、解：（1）方程两边同时乘x（x+1），
得2x﹣（x+1）＝0，
化简，得x﹣1＝0，
解得x＝1．
检验：把x＝1代入x（x+1），得1×2＝2≠0，
∴原分式方程的解为x＝1．
（2）方程两边同时乘x﹣4，
得﹣3+2（x﹣4）＝1﹣x，
化简，得﹣3+2x﹣8＝1﹣x，
整理，得3x＝12，
解得x＝4．
检验：把x＝4代入x﹣4，得4﹣4＝0，
∴原分式方程无解．
19、解：


，
∵x2﹣4≠0，x+2≠0，x﹣1≠0，
∴x≠±2且x≠1，
∵2≥x≥﹣2，且x为整数，
∴x＝﹣1或0，
当x＝﹣1时，原式；
当x＝0时，原式．
20、解：（1）如图：即为所求作的图形．

(2)证明：如图，在中，，

∴，
∵EF是线段AC的垂直平分线，
∴，，
在和中，
，
∴，
∴，
∴四边形是平行四边形，
又∵，
∴四边形是菱形．
21、（1）证明：四边形是平行四边形，
，，，
，
，分别是，的中点，
，
在和中，
，
；
（2）证明：由（1）知，
，，
，
，
，即，
，
四边形是平行四边形，
．
22、（1）解：∵反比例函数y的图象经过点A（﹣3，2），
∴m＝﹣3×2＝﹣6，
∵点B（1，n）在反比例函数图象上，
∴n＝﹣6．
∴B（1，﹣6），
把A，B的坐标代入y＝kx+b，则，
解得k＝﹣2，b＝﹣4，
∴一次函数的解析式为y＝﹣2x﹣4，反比例函数的解析式为y；
（2）解：如图，设直线AB交y轴于C，

则C（0，﹣4），
∴S△AOB＝S△OCA+S△OCB4×34×1＝8；
（3）解：观察函数图象知，
不等式kx+b的解集为x＜﹣3或0＜x＜1．
23、（1）证明：由对折的性质可得，△ABD≌△ABE，△ACD≌△ACF，
∴∠DAB＝∠EAB，∠DAC＝∠FAC，
∵∠BAC＝45°，
∴∠EAF＝90°，
∵AD⊥BC，
∴∠E＝∠ADB＝90°，∠F＝∠ADC＝90°，
∴四边形AEGF为矩形，
∵AE＝AD，AF＝AD，
∴AE＝AF，
∴矩形AEGF是正方形；
（2）解：根据对称的性质可得：BE＝BD＝2，CF＝CD＝3，
设AD＝x，则正方形AEGF的边长是x，
则BG＝EG−BE＝x−2，CG＝FG−CF＝x−3，
在Rt△BCG中，根据勾股定理可得：（x−2）2＋（x−3）2＝52，
解得：x＝6或−1（舍去）．
∴AD＝6．
24、（1）解：①∵A（﹣3，8），C（6，﹣4），
∴﹣3×8＝﹣24，6×（﹣4）＝﹣24，
∴A、C满足同一个反比例函数，
②∵A（1，2），C（2，3），
∴1×2＝2，2×3＝6，
∴A、C不满足同一个反比例函数，
③∵A（3，4），C（2，6），
∴3×4＝12，2×6＝12，
∴A、C满足同一个反比例函数，
∴可能是某反比例函数的“伴随矩形”的是①③，
故答案为：①③；
（2）解：∵B（2，）的反比例函数y＝的“伴随矩形”ABCD的顶点，
∴A（2，3），C（4，），
∴D（4，3），
设直线BD的解析式为y＝kx+b，
则，
∴，
∴y＝；
（3）证明：∵A、C在反比例函数y＝上，
设A（m，），C（n，），则B（m，），D（n，），
设直线BD的解析式为＝cx+d，
则，
∴，
即y＝，
∴直线BD过原点．
25、解：（1）∵当x＞0时，随着x的增大而减小，
∴随着x的增大，1的值减小；
∵当x＜0时，随着x的增大而减小，
∵1，
∴随着x的增大，的值减小，
故答案为：减小，减小；
（2）∵2，
∵当x＞1时，的值无限接近0，
∴的值无限接近2；
（3）∵5，
又∵0≤x≤2，
∴﹣13，
∴﹣8．
故答案为：﹣8．
26、解：（1）①∵正方形ADEF中，AD＝AF，
∵∠BAC＝∠DAF＝90°，
∴∠BAD＝∠CAF，
在△DAB与△FAC中，
，
∴△DAB≌△FAC（SAS），
∴∠B＝∠ACF，
∴∠ACB+∠ACF＝90°，即BC⊥CF；
故答案为：BC⊥CF；
②∵△DAB≌△FAC，
∴CF＝BD，
∵BC＝BD+CD，
∴BC＝CF+CD；
故答案为：BC＝CF+CD；
（2）CF⊥BC成立；BC＝CD+CF不成立，CD＝CF+BC．理由如下：
∵正方形ADEF中，AD＝AF，
∵∠BAC＝∠DAF＝90°，
∴∠BAD＝∠CAF，
在△DAB与△FAC中，
，
∴△DAB≌△FAC（SAS），
∴∠ABD＝∠ACF，
∵∠BAC＝90°，AB＝AC，
∴∠ACB＝∠ABC＝45°．
∴∠ABD＝180°﹣45°＝135°，
∴∠BCF＝∠ACF﹣∠ACB＝135°﹣45°＝90°，
∴CF⊥BC．
∵CD＝DB+BC，DB＝CF，
∴CD＝CF+BC．
（3）解：过A作AH⊥BC于H，过E作EM⊥BD于M，EN⊥CF于N，如图3所示：

∵∠BAC＝90°，BC＝4，
∴AB＝AC＝2，
∵AH⊥BC，
AHBC＝BH＝CH＝2，
∴DH＝CH+CD＝3，
∵四边形ADEF是正方形，
∴AD＝DE，∠ADE＝90°，
∵BC⊥CF，EM⊥BD，EN⊥CF，
∴四边形CMEN是矩形，
∴NE＝CM，EM＝CN，
∵∠AHD＝∠ADC＝∠EMD＝90°，
∴∠ADH+∠EDM＝∠EDM+∠DEM＝90°，
∴∠ADH＝∠DEM，
∴△ADH≌△DEM（AAS），
∴EM＝DH＝3，DM＝AH＝2，
∴CN＝EM＝3，EN＝CM＝3，
∵∠ABC＝45°，
∴∠BGC＝45°，
∴△BCG是等腰直角三角形，
∴CG＝BC＝4，
∴GN＝1，
在Rt△EGN中，EG．