


沪教版 (五四制)六年级下册7.2 画线段的和、差、倍备课ppt课件
展开问题: 学生张凯和王鹏各带了一把折扇(如图),下面是他们的一段对话:
张:我的折扇大一些,所以我的折扇的角 也大一些.
王:我的折扇长一些,所以我的折扇的角也大一些.
同学们,你们有办法帮他们进行判断吗?
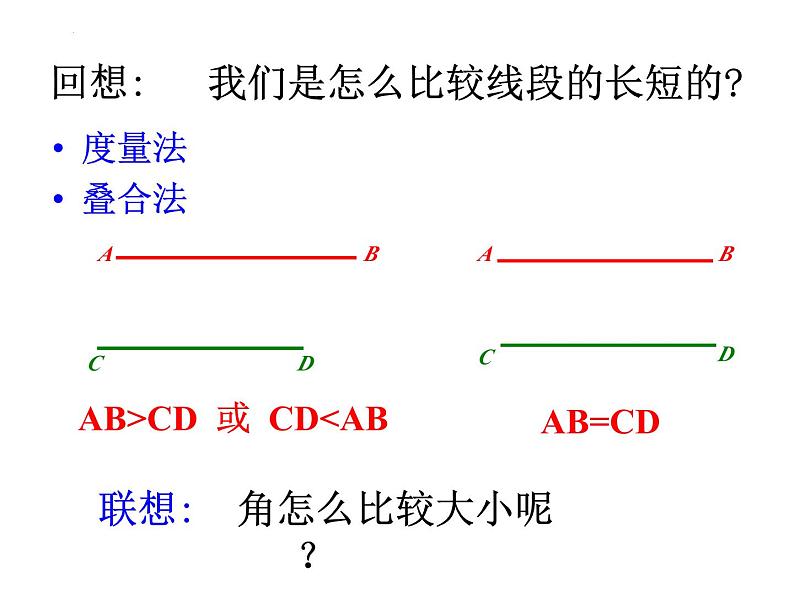
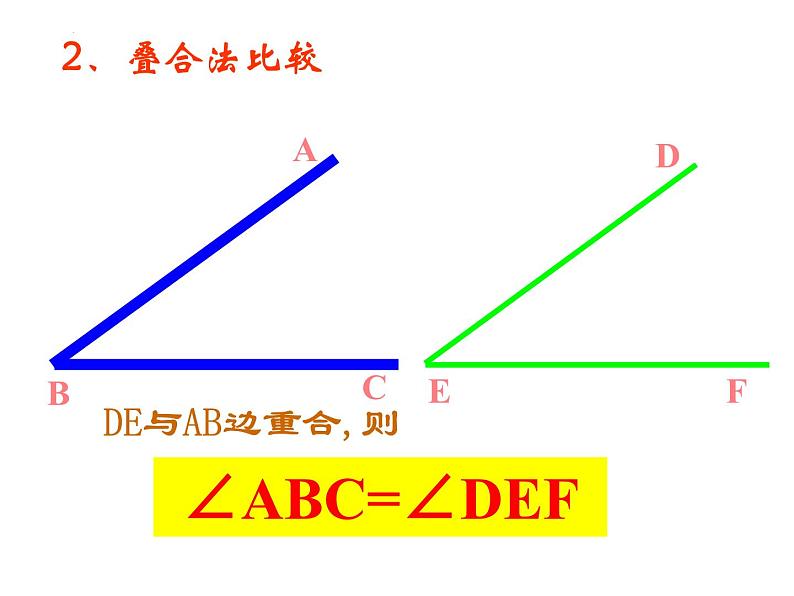
怎样比较∠ABC和∠DEF的大小?
我们是怎么比较线段的长短的?
AB>CD 或 CD
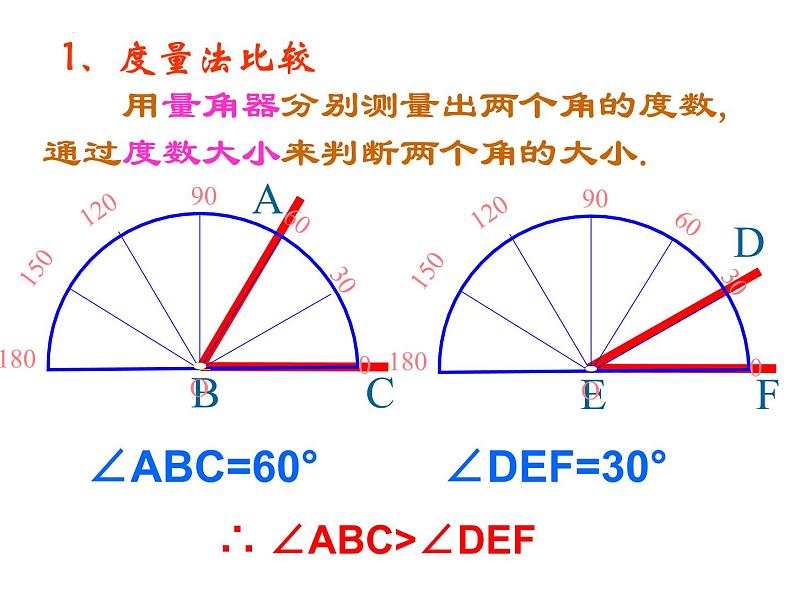
∴ ∠ABC>∠DEF
用量角器分别测量出两个角的度数,通过度数大小来判断两个角的大小.
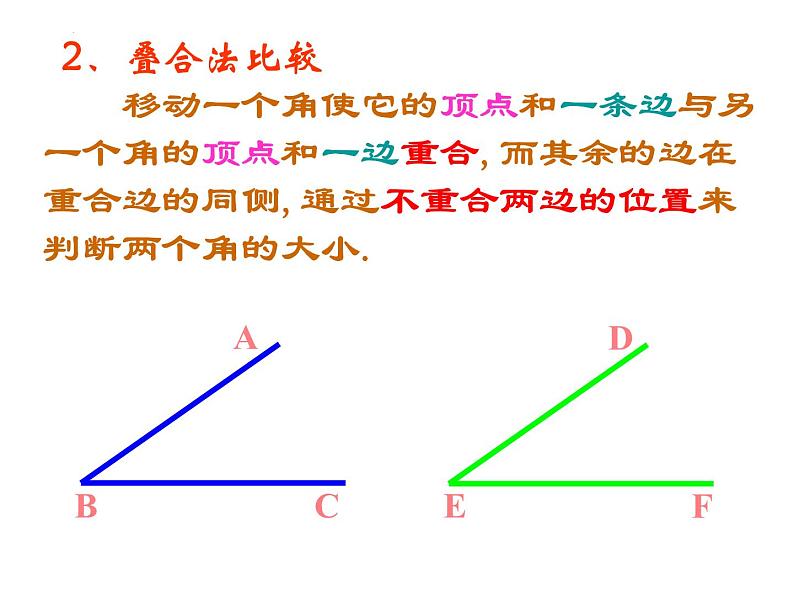
移动一个角使它的顶点和一条边与另一个角的顶点和一边重合,而其余的边在重合边的同侧,通过不重合两边的位置来判断两个角的大小.
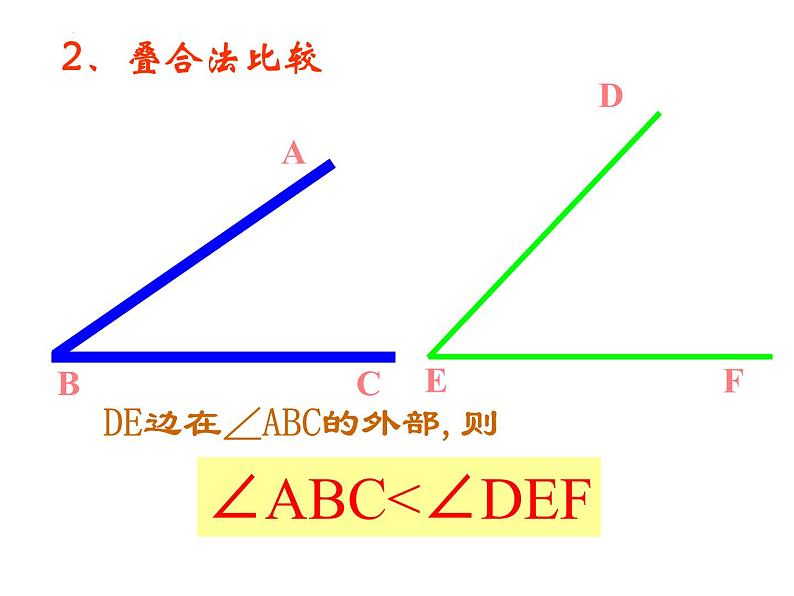
DE边在∠ABC的外部,则
DE边在∠ABC的内部,则
回到开始的问题,学生张凯和王鹏的对话中说的折扇的大小和长短能判断角的大小吗?
张:我的折扇大一些,所以我的折扇的角也大一些.
结论:角的大小与角的两边张开的大小一致,与所画边的长短无关
例1、估计图中∠1与∠2的大小关系,并用适当的方法检查。
练习:如图,用〝=〞或 〝>〞或 〝<〞填空
(1)用量角器量出∠α的度数
(2)画出∠AOB=57°
例题:如图,已知∠α,画一个角等于∠α.
(1)用量角器画∠AOB,使∠AOB= ∠α.
② 用量角器作另一边OB; (对中、对边、度数)
(2)以∠α 的顶点为圆心,以取定的长a为半径,作弧分别交∠α两边于E、F;
(3)以点O为圆心,以a为半径作弧,交OC于点M;
(4)以点M为圆心,以EF长为半径作弧,交前弧于点N
(5)经过点N作射线OD;
(2)用直尺、圆规画∠COD= ∠α.
(2)用直尺、圆规∠COD= ∠α.
所以,∠COD就是所求作的角.
例2:用尺规作图做出一个和∠1大小相等的∠AOB,并且OA=a,OB=b;
一、回顾线段和差倍的画法和意义
两条线段的和(或差)也是一条线段;
其长度等于这两条线段的长度的和(或差)。
线段OB就是所要画的线段a-b
线段OB就是所要画的线段a+b
两个角的和(或差)也是一个角,角的度数等于这两个角的度数的和(或差)。一个角的a倍也是一个角,角的度数等于这个角的a倍。
例题1:如图,已知∠α、∠β,画一个角,使它(1)等于∠α+∠β.
二、新授画角的和、差、倍
②以点B为顶点,射线BC为一边,在∠ ABC的外部用量角器画∠CBD= ∠β 。
解:①用量角器画出∠ABC= ∠α;
∠ABD就是所要画的角.
试一试:如果要画一个角等于2∠α-∠β呢?
②以点B为顶点,射线BC为一边,在∠ ABC的 外部 用量角器画∠CBD= ∠β 。
线段中点将这条线段分成相等的两部分.
已知点M是线段AB的中点,那么AM=______=_____AB,AB=____AM=___MB.
角是否也有将其分成相等两部分的图形呢?
操作: 用纸片作材料任意剪一个角,折叠这张纸片,使角的两边叠合在一起,再展开摊平,可以看到什么?
经过折叠,折痕所在的射线将一个角分成了两个相等的角.
从一个角的顶点引出一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.
因为 OC是∠AOB的平分线,
(也可以说OC平分∠AOB )
所以 ∠AOC=∠BOC,
∠AOB=2∠AOC,
∠AOC= ∠AOB
∠BOC= ∠AOB
∠AOB=2∠BOC.
怎样画出一个角的角平分线呢?
例1 如图,已知∠AOB,画出它的角平分线.
解 ⑴用量角器量得∠AOB =48°;
⑵在∠AOB的内部画射线OM,使∠AOM =24°.
射线OM就是所要画的∠AOB的平分线.
解 ⑴以∠AOB的顶点为圆心,以取定的长a为半径,作弧分别交∠AOB的两边于点D、E;
⑵分别以点D、点E为圆心,以大于 DE的同一长度为半径作弧,两弧交于∠AOB的内的一点C;
射线OC就是所求作的∠AOB的平分线.
如图,∠AOD=80°,∠COD=30°,OB是∠AOC的平分线, 那么∠AOC=( )°, ∠AOB=( )°.
∠AOC= ∠AOD—∠COD
因为OB是∠AOC的平分线,
所以∠AOB= ∠AOC
一般地,如果两个角的和等于90°(直角),就说这两个角互为余角.即其中每一个角都是另一个角的余角。
请你判断:(1)∠1+∠2=90°则∠1是余角.( ) (2) ∠1 +∠2+ ∠3=90°,则∠1 、∠2、 ∠3、互为余角.( )
∠1是∠2的余角, 或∠2是∠1的余角
几何语言表示为:若∠1+∠2=90°,那么∠1与∠2互为余角
∠1 = 90°—∠2
或:若∠1与∠2互为余角,那么∠1+∠2=90°
图中给出的各角,那些互为余角?
一般地,如果两个角的和等于180°(平角),就说这两个角互为补角.即其中一个是另一个角的补角。
若∠1+∠2=180°,则∠1与∠2互为补角
∠1 = 180°—∠2
反过来说也成立:若∠1与∠2互为补角,那么∠1+∠2=180°
图中给出的各角,那些互为补角?
2、互补的两个角不可能相等。( )
3、钝角没有余角,但一定有补角( )
1、如果一个角有补角,那么这个角一定是钝角( )
▲锐角既有余角又有补角; ▲相等的两个角互补, 这两个角是直角;
1、已知:一个锐角的补角加上 后等于 求:这个角的度数
2.已知∠α= 60°32′则∠α的余角等于_____ 。则∠α的补角等于________.
1°=60′(分),1′=60″(秒)
沪教版 (五四制)六年级下册6.10 三元一次方程组及其解法课文内容ppt课件: 这是一份沪教版 (五四制)六年级下册6.10 三元一次方程组及其解法课文内容ppt课件,共40页。PPT课件主要包含了直线射线线段,线段的大小的比较,线段AB,线段a,建立模型感受新知,度量法,叠合法,实践操作探索新知,三步骤,画射线等内容,欢迎下载使用。
初中数学沪教版 (五四制)六年级下册5.9 有理数的混合运算教课内容课件ppt: 这是一份初中数学沪教版 (五四制)六年级下册5.9 有理数的混合运算教课内容课件ppt,共40页。PPT课件主要包含了×2×2,n个a,记作210,有理数的乘方,读作a的n次方,a×a×a···×a,乘方的意义,有理数混合运算顺序,观察图片,科学计数法步骤等内容,欢迎下载使用。
沪教版 (五四制)六年级下册5.8 有理数的乘方教学演示ppt课件: 这是一份沪教版 (五四制)六年级下册5.8 有理数的乘方教学演示ppt课件,共26页。PPT课件主要包含了水库水位的变化,归纳,有理数的乘法法则,课堂练习,乘积的符号的确定,负因数的个数,有理数乘法的运算律,有理数除法法则,合作探究等内容,欢迎下载使用。













