






2024全国一轮数学(基础版)第35讲 直线、平面垂直的判定与性质课件PPT
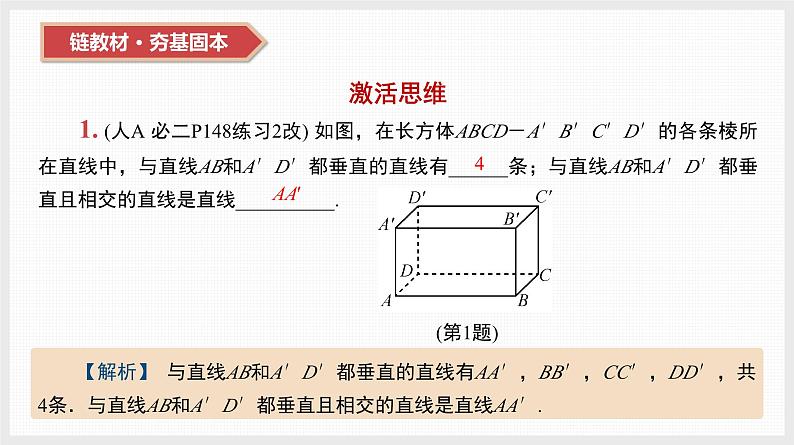
展开1. (人A 必二P148练习2改) 如图,在长方体ABCD-A′B′C′D′的各条棱所在直线中,与直线AB和A′D′都垂直的直线有______条;与直线AB和A′D′都垂直且相交的直线是直线__________. (第1题)
【解析】 与直线AB和A′D′都垂直的直线有AA′,BB′,CC′,DD′,共4条.与直线AB和A′D′都垂直且相交的直线是直线AA′.
2. (人A 必二P152练习4)过△ABC所在平面α外一点P,作PO⊥α,垂足为O,连接PA,PB,PC.(1) 若PA=PB=PC,则点O是△ABC的______心.
【解析】如图,因为PO⊥α,所以PO⊥AO,PO⊥BO,故∠POA=∠POB=90°.又PA=PB,PO=PO,所以△POA≌△POB,可得OA=OB,同理可得OA=OC,所以点O是△ABC的外心.
【解析】由(1)可得点O是△ABC的外心.因为∠C=90°,在直角三角形中,斜边的中线是斜边的一半,所以点O为斜边的中点,即为AB边的中点.
(2) 若PA=PB=PC,∠C=90°,则点O是AB边的________.
【解析】因为PA⊥PB,PB⊥PC,且PA∩PC=P,PA,PC⊂平面PAC,所以PB⊥平面PAC,所以PB⊥AC.因为PO⊥α,所以PO⊥AC.又PB∩PO=P,PB,PO⊂平面PBO,所以AC⊥平面PBO,所以BO⊥AC,同理可得CO⊥AB,AO⊥BC,故点O是△ABC的垂心.
(3) 若PA⊥PB,PB⊥PC,PC⊥PA,垂足都为P,则点O是△ABC的______心.
3. (人A 必二P162练习2)若平面α⊥平面β,且α∩β=l,则下列命题中真命题的个数是( )①平面α内的任一条直线必垂直于平面β;②平面α内的直线必垂直于平面β内的任意一条直线;③平面α内的已知直线必垂直于平面β内的无数条直线;④过平面α内任意一点作交线l的垂线,则此垂线必垂直于平面β.A. 0 B. 1 C. 2 D. 3
【解析】 ①在平面α内取与l平行的直线,其不垂直于平面β,故①是假命题;②当在平面α内取平行于交线l的直线时,该直线与平面β平行,故②是假命题;③取平面β内无数条与交线l垂直的直线,平面α内的已知直线与这无数条直线垂直,故③是真命题;④若α内的任意一点取在交线l上,所作垂线可能不在平面α内,所以不一定垂直于平面β,故④是假命题.
4. (人A 必二P162练习1改)(多选)下列选项正确的是( )A. 垂直于同一条直线的两条直线平行B. 如果平面α⊥平面β,那么平面α内所有直线都垂直于平面βC. 如果平面α⊥平面β,那么平面α内一定存在直线平行于平面βD. 如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β
【解析】 对于A,垂直于同一条直线的两条直线可能平行、相交、异面,故A错误;对于B,若平面α⊥平面β,则两平面一定相交,设交线为直线a,显然a⊂α,但直线a与平面β不垂直,故B错误;对于C,平面α⊥平面β,若它们的交线记为直线l,因此直线l⊂平面β,在平面α内一定有直线m∥l,则直线m∥平面β,故C正确;对于D,若平面α内存在直线垂直于平面β,则根据面面垂直的判定定理可知α⊥β,所以如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β,故D正确.
5. (人A 必二P155练习1)已知直线a,b和平面α,若a⊥b,a⊥α,则b与α的位置关系是______________.
【解析】 若b⊂α,a⊥α,则a⊥b;若b∥α,过b作平面β,使得α∩β=c,由a⊥α,c⊂α,得a⊥c,又b∥c,则a⊥b.
1. 直线与平面垂直(1) 直线与平面垂直的定义:直线l与平面α内的________________都垂直,就说直线l与平面α互相垂直.
2. 直线和平面所成的角(1) 定义:一条斜线和它在平面上的射影所成的________叫做这条直线和这个平面所成的角,一条直线垂直于平面,则它们所成的角是直角;一条直线和平面平行或在平面内,则它们所成的角是0°的角. (2) 取值范围:________.
3. 二面角(1) 定义:从一条直线出发的______________所组成的图形叫做二面角.(2) 二面角的平面角:以二面角的棱上任一点为端点,在两个半平面内分别作____________的两条射线,这两条射线所成的角叫做二面角的平面角.(3) 二面角的取值范围:______________.(4) 平面与平面垂直的定义:两个平面相交,如果它们所成的二面角是____________,就说这两个平面互相垂直.4. 点面距:点与它在平面上的投影的距离.
5. 平面与平面垂直的判定定理和性质定理
6. 常用结论(1) 若两平行线中的一条垂直于一个平面,则另一条也垂直于这个平面(需要证明不可直接用).(2) 若一条直线垂直于一个平面,则它垂直于这个平面内的任何一条直线(证明线线垂直的一个重要方法).(3) 垂直于同一条直线的两个平面平行.
例1 如图,在四棱锥P-ABCD中,AC∩BD=O,底面四边形ABCD为菱形.试在①PA⊥BD,②PC⊥AB,③PA=PC三个条件中选两个条件,使得PO⊥平面ABCD成立,并说明理由.(例1)
【解答】 若选条件②,利用反证法:由PO⊥平面ABCD,AB⊂平面ABCD,得PO⊥AB.又PC⊥AB,PO∩PC=P,所以AB⊥平面PAC.因为AC⊂平面PAC,所以AB⊥AC,由菱形的性质可得BD⊥AC,所以AB∥BD,与AB∩BD=B矛盾,故不选条件②.若选条件①③,理由如下:由底面ABCD为菱形,得BD⊥AC.又BD⊥PA,PA∩AC=A,所以BD⊥平面PAC.又PO⊂平面PAC,所以BD⊥PO.因为PA=PC,AO=CO,所以PO⊥AC.又BD∩AC=O,所以PO⊥平面ABCD.
证明线面垂直的常用方法及关键:(1) 证明直线和平面垂直的常用方法:①判定定理;②垂直于平面的传递性(a∥b,a⊥α⇒b⊥α);③面面平行的性质(a⊥α,α∥β⇒a⊥β);④面面垂直的性质.(2) 证明线面垂直的关键是证明线线垂直,而证明线线垂直则需借助线面垂直的性质.
【解答】 因为AA1⊥平面ABC,BC⊂平面ABC,所以AA1⊥BC.因为AB∩AA1=A,所以BC⊥平面ABB1A1.又A1D⊂平面ABB1A1,所以BC⊥A1D.
【解答】 如图,取BC的中点F,连接AF,DF.又因为BD⊥PC,CD∩PC=C,所以BD⊥平面PCD.又因为PD⊂平面PCD,所以BD⊥PD.又因为平面PBD⊥平面ABCD,且平面PBD∩平面ABCD=BD,所以PD⊥平面ABCD.又因为PD⊂平面PAD,所以平面PAD⊥平面ABCD.
(1) 判定面面垂直的方法:①面面垂直的定义;②面面垂直的判定定理.(2) 面面垂直性质的应用:①面面垂直的性质定理是把面面垂直转化为线面垂直的依据,运用时要注意“平面内的直线”. ②若两个相交平面同时垂直于第三个平面,则它们的交线也垂直于第三个平面.
又因为BD∩PB=B,所以BC⊥平面PBD.因为BC⊂平面PBC,所以平面PBC⊥平面PBD.
2. 如图,在四棱锥P-ABCD中,AB∥CD,∠ABC=90°, △PDC是等边三角形,平面PDC⊥平面ABCD,E为PC的中点.设平面PAD∩平面PBC=l,求证:DE⊥l.(第2题)
【解答】 因为AB∥CD,∠ABC=90°,所以BC⊥CD.又平面PDC⊥平面ABCD,且平面PDC∩平面ABCD=DC,BC⊂平面ABCD,所以BC⊥平面PDC.又BC⊂平面PBC,从而平面PDC⊥平面PBC.因为△PDC为等边三角形,E为PC的中点,所以DE⊥PC,因为平面PDC∩平面PBC=PC,DE⊂平面PDC,故DE⊥平面PBC.由已知l⊂平面PBC,所以DE⊥l.
因为PD⊥底面ABCD,AM⊂平面ABCD,所以AM⊥PD.又PD∩DB=D,PD,DB⊂平面PDB,从而有AM⊥平面PDB.又AM⊂平面PAM,所以平面PAM⊥平面PDB.
【解答】 如图(1),取BC的中点D,连接AD,B1D. (例3(1))因为BC=2B1C1,所以DC=B1C1,又BC⊥CC1,且DC∥B1C1,则四边形DCC1B1为矩形,故B1D⊥BD.又AB=BC=CA,所以AD⊥BD.因为B1D,AD⊂平面B1AD,故BD⊥平面B1AD,又AB1⊂平面B1AD,故AB1⊥BC.
(1) 求证:AB1⊥BC;
【解答】 由(1)知BD⊥平面B1AD,故二面角C1-BC-A的平面角即为∠ADB1=60°.
(2) 若二面角C1-BC-A的平面角为60°,求直线AC1与平面BCC1B1所成角的正弦值.
又AE⊂平面ADB1,BD⊥平面ADB1,所以BD⊥AE.因为BD∩ED=D,BD,ED⊂平面BCC1B1,从而AE⊥平面BCC1B1,
例4 如图,在多面体ABCDEF中,底面ABCD是菱形,∠ABC=60°,FA⊥平面ABCD,ED∥FA,且AB=FA=2ED=2.(例4)
【解答】 如图,连接BD交AC于点O,设FC的中点为P,连接OP,EP.因为FA⊥平面ABCD,BD⊂平面ABCD,所以FA⊥BD.因为四边形ABCD是菱形,所以BD⊥AC.因为FA∩AC=A,FA,AC⊂平面FAC,所以BD⊥平面FAC,即EP⊥平面FAC.又EP⊂平面EFC,所以平面FAC⊥平面EFC.
(1) 求证:平面FAC⊥平面EFC;
(2) 求多面体ABCDEF的体积.
垂直关系的应用,涉及点面距和线面角的计算,其中线面角主要是要找到平面角,距离问题则是通过线面垂直找到锥体的高.
1. 已知两条异面直线平行于同一平面,一直线与两异面直线都垂直,那么这个平面与这条直线的位置关系是( )A. 平行 B. 垂直C. 斜交 D. 不能确定
点击对应数字即可跳转到对应题目
2. 已知l,a,b是三条不同的直线,α,β是两个不重合的平面,则l⊥α的一个充分条件可以是( )A. a⊂α,b⊂α,a⊥l,b⊥l B. β⊥α,l∥βC. l⊥β,β∥α D. a∥α,l⊥a
3. 设m,n是两条不同的直线,α,β是两个不重合的平面,则下列说法正确的是( )A. 若α⊥β,m⊂α,n⊂β,则m⊥nB. 若m⊥α,m∥n,n∥β,则α⊥βC. 若m⊥n,m⊂α,n⊂β,则α⊥βD. 若α∥β,m⊂α,n⊂β,则m∥n
4. (2022·无锡期末)在正方体ABCD-A1B1C1D1中,设M是正方形ABCD的中心,则直线B1M与平面A1C1B所成角的正弦值为( )
【解析】 如图,因为B1D在平面A1B1C1D1内的射影为B1D1,又B1D1⊥A1C1,所以B1D⊥A1C1,同理可证B1D⊥A1B.又A1C1∩A1B=A1,所以B1D⊥平面A1C1B, 所以B1M与平面A1C1B所成角的正弦值等于B1M与B1D所成角的余弦值,即求∠MB1D的余弦值的绝对值.
5. (多选)已知P为△ABC所在平面外一点,且PA,PB,PC两两互相垂直,下列结论中正确的是( )A. PA⊥BC B. PB⊥ACC. PC⊥AB D. AB⊥BC
【解析】 如图,因为PA⊥PB,PA⊥PC,PB∩PC=P,且PB⊂平面PBC,PC⊂平面PBC,所以PA⊥平面PBC.又BC⊂平面PBC,所以PA⊥BC,同理可得PB⊥AC,PC⊥AB.
2024年新高考数学第一轮复习课件:第35讲 直线、平面垂直的判定与性质: 这是一份2024年新高考数学第一轮复习课件:第35讲 直线、平面垂直的判定与性质,共26页。PPT课件主要包含了答案D,答案AD,答案AC等内容,欢迎下载使用。
2024全国一轮数学(基础版)第34讲 直线、平面平行的判定与性质课件PPT: 这是一份2024全国一轮数学(基础版)第34讲 直线、平面平行的判定与性质课件PPT,共37页。PPT课件主要包含了链教材·夯基固本,激活思维,第4题,基础回归,3性质定理,研题型·融会贯通,举题说法,随堂内化,第5题等内容,欢迎下载使用。
高考数学(理)一轮复习课件+讲义 第8章 第5讲 直线、平面垂直的判定与性质: 这是一份高考数学(理)一轮复习课件+讲义 第8章 第5讲 直线、平面垂直的判定与性质,文件包含高考数学理一轮复习课件第8章第5讲直线平面垂直的判定与性质pptx、高考数学理一轮复习讲义第8章第5讲直线平面垂直的判定与性质doc等2份课件配套教学资源,其中PPT共60页, 欢迎下载使用。












