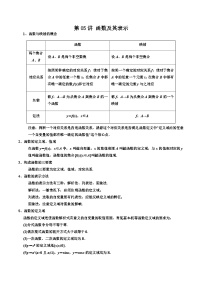
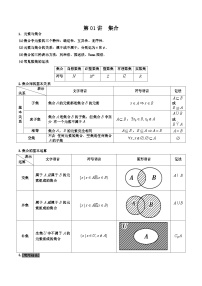
高考数学一轮复习基础版讲义（适合艺术生、基础生一轮复习）——空间向量在空间几何的应用二

这是一份高考数学一轮复习基础版讲义（适合艺术生、基础生一轮复习）——空间向量在空间几何的应用二，文件包含第34讲空间向量在空间几何中的运用解答题含探索性问题解析版docx、第34讲空间向量在空间几何中的运用解答题含探索性问题原卷版docx等2份试卷配套教学资源，其中试卷共28页， 欢迎下载使用。
第34讲 空间向量在空间几何中的运用二1．（全国高二课时练习）如图,三棱柱中,平面平面,且,,求异面直线与所成角的余弦值. 【答案】【详解】以为坐标原点,所在直线分别为轴、轴,建立如图所示的空间直角坐标系,则,所以.设所求的角为,则,即异面直线与所成角的余弦值为.2．（浙江高二单元测试）在正三棱柱中，若，求与所成角的大小.【答案】【详解】由题意可得，平面；设，则，又，，所以.故.即，即与所成角的大小为. 3．（惠来县华侨中学高二月考）如图，在棱长为2的正方体中，为棱的中点，为棱的中点．（1）求直线与直线所成角的余弦值.（2）求证：平面；【答案】（1）；（2）证明见解析.【详解】(1) 以为原点，分别为轴，建立如图空间直角坐标系，则，，，，，，，因为E为棱BC的中点，F为棱CD的中点，所以，，所以，，∴，，即直线与所成角的余弦值为；（2）设平面的一个法向量为，又，，则，令，则，因为，所以，因为平面，所以平面；  4．（全国高二单元测试）如图，正方体中，是的中点，求与平面所成角的正弦值.【答案】.【详解】如图，建立空间直角坐标系，设正方体的棱长为2，则.设平面的法向量为，令，则，.故与平面所成角的正弦值为.5．（浙江高三专题练习）如图，四棱锥中，是正三角形，四边形是菱形，点是的中点.（I）求证：// 平面；（II）若平面平面，，求直线与平面所成角的正弦值.【答案】（I）证明见解析；（II）.【详解】（I）证明：连接BD角AC于点F，再连接EF.因为四边形是菱形，所以点F是BD的中点，又因为点是的中点，所以EF是三角形DBS的中位线，所以DS平行EF，又因为EF平面ACE，SD平面ACE所以// 平面（II）因为四边形是菱形，，所以 又AB=AD，所以三角形ABD为正三角形.取AB的中点O，连接SO，则DOAB因为平面平面，平面平面=AB所以DO平面ABS，又因为三角形ABS为正三角形则以O为坐标原点建立坐标系设AB=2a，则 设平面ADS的一个法向量为 则 取x=1，则 所以设直线AC与平面ADS所成角为 则6．（吉林白城一中）如图，四棱锥中，为正三角形，为正方形，平面平面，、分别为、中点.（1）证明：平面；（2）求直线与平面所成角的正弦值.【答案】(1)见解析;(2).详解：（1）连接，∵是正方形，是的中点，∴是的中点，∵是的中点，∴，∵平面，平面，∴平面.（2）建立如图所示空间直角坐标系，设，则，，，，，，，设平面的法向量，则，取得，设与平面所成角为，则.7．（莆田锦江中学高二期末）在直三棱柱中，，，，点是的中点；（I）求异面直线，所成角的余弦值；（II）求直线与平面所成角的正弦值．【答案】（I）（II）解：（I）以，，为x，y，z轴建立空间直角坐标系A﹣xyz，则可得B（2，0，0），A1（0，0，4），C1（0，2，4），D（1，1，0），∴=（2，0，﹣4），=（0，2，4），∴cos＜，＞==∴异面直线A1B，AC1所成角的余弦值为：；（II）由（I）知，=（2，0，﹣4），=（1，1，0），设平面C1AD的法向量为=（x，y，z），则可得，即，取x=1可得=（1，﹣1，），设直线AB1与平面C1AD所成的角为θ，则sinθ=|cos＜，＞|=∴直线AB1与平面C1AD所成角的正弦值为：8．（黔西南州同源中学（理））如图所示，平面，四边形为矩形，，，．（1）求证：平面；（2）求平面与平面所成锐二面角的余弦值．【答案】（1）见解析（2）【详解】（1）∵四边形ABEF为矩形又平面ADE，AE平面ADE平面ADE又，同理可得：平面ADE又，BF，BC 平面BCF∴平面平面ADE又CF平面BCF平面ADE（2）如图，以A为坐标原点，建立空间直角坐标系，则，， ,,设是平面CDF的一个法向量，则即令，解得又是平面AEFB的一个法向量，∴平面CDF与平面AEFB所成锐二面角的余弦值为.9．（浙江高三专题练习）如图，在四棱锥中，底面是矩形，是的中点，平面，且，．（）求与平面所成角的正弦．（）求二面角的余弦值．【答案】(1) .(2) .详解：（）∵是矩形，∴，又∵平面，∴，，即，，两两垂直，∴以为原点，，，分别为轴，轴，轴建立如图空间直角坐标系，由，，得，，，，，，则，，，设平面的一个法向量为，则，即，令，得，，∴，∴，故与平面所成角的正弦值为．（）由（）可得，设平面的一个法向量为，则，即，令，得，，∴，∴，故二面角的余弦值为．10．（江西九江一中高二月考（理））如图，四棱锥的底面是矩形，底面，，，为的中点．（1）求证：；（2）求平面与平面所成的角的余弦值．【答案】（1）证明见解析；（2）．【详解】解：（1）依题意，棱DA，DC，DP两两互相垂直.以点D为原点，依次以DA，DC，DP所在直线为x，y，z轴，如图，建立空间直角坐标系.则，，，.可得，.所以，所以 （2）由（1）得到，，因此可得，.设平面的一个法向量为，则由得令，解得.同理，可求平面PDC的一个法向量.所以，平面PAM与平面PDC所成的锐二面角满足：.即平面PAM与平面PDC所成的锐二面角的余弦值为.11．（西城·北京四中）如图，在四棱柱，底面，，，且，点在棱上，平面与棱相交于点.（Ⅰ） 证明：平面；（Ⅱ）棱上是否存在点，使二面角的余弦值为？若存在，求出的值；若不存在，说明理由.（Ⅲ）求三棱锥的体积的最大值.【答案】（Ⅰ）证明见解析；（Ⅱ）存在，；（Ⅲ）当F与重合时，体积最大值为.【详解】（Ⅰ）因为平面与棱相交于点，所以平面，在四棱柱中，因为平面平面，平面平面，平面平面，所以，又因为平面，平面，所以平面；（Ⅱ）因为底面，，所以以为原点，分别为轴，轴，轴建立空间直角坐标系，则，所以，设面的法向量为，则，即，取，则，所以，取面的一个法向量，因为二面角的余弦值为，所以，解得或，因为，所以，即为棱的中点时，二面角的余弦值为，所以.（Ⅲ）过作于点，因为面面，面面，面面，，所以面，所以，因为与重合时，取得最大值，所以与重合时，三棱锥的体积最大，最大为.12．（武汉市育才高级中学高二月考）如图，在四棱锥中，底面是直角梯形，侧棱底面，垂直于和，为棱上的点，，．（1）当时，求平面与平面所成的锐二面角的余弦值；（2）在第（1）问条件下，设点是线段上的动点，与平面所成的角为，求当取最大值时点的位置．【答案】（1）；（2）【详解】由题设，面，又面，则，，又，又，则面，由面，面面，则面面，∴可构建以为原点，为x、y、z轴正方向的空间直角坐标系，如下图示：由，，，且，∴，（1），若是面的一个法向量，则，令，即，又是面的一个法向量，∴，故面与平面所成的锐二面角的余弦值为.（2）若，则，故，由（1）知：令，则，∴，若，∴，则时取最大， 此时，，可得，即，∴，则.13．（北京市陈经纶中学高二月考）在四棱锥中，底面ABCD为长方形，底面ABCD，，；的可能取值为：①；②；③；④；⑤．已知线段CD上存在点E，满足．（1）求t的所有可能取值，并说明理由；（2）当t为所有可能取值的最大值时，线段上满足的点有两个，分别记为，，求二面角的大小．【答案】（1）t可以取①②③；理由见解析；（2）30°．【详解】（1）如图所示，以BC，BA，BP的方向分别为x轴，y轴，z轴正方向建立空间直角坐标系．则各点坐标分别为， ，，．设，所，，．∴，∴， ∴在所给的数据中，t可以取①②③．（2）由（1）知，此时或．根据题意得，其坐标为和，∵底面ABCD，∴，，∴是二面角的平面角，由，由题意得，二面角为锐角，所以二面角的大小为30°．14．（东城·北京二中高二月考）如图，在四棱锥中，底面为直角梯形，且，，侧面底面.若.（1）求证：平面；（2）求平面和平面夹角的余弦值；（3）点是侧棱上一点，且直线和平面所成角的大小为30°，求的值.【答案】(1)证明见解析；(2)；(3).【分析】【详解】(1)因，即，而平面平面，平面平面，平面，则平面，而平面，即有，在直角梯形中，且，又，令，则，，中， 由余弦定理得，于是有，即，而，平面PAC，所以平面；(2)由(1)知，AB，AD，AP两两垂直，以点A为原点，向量的方向分别为x，y，z轴正方向建立空间直角坐标系，如图，令，则，，设平面的法向量，则，令，得，而平面的法向量，于是得，显然平面和平面夹角为锐角，所以平面和平面夹角的余弦值是；(3)由(2)知，，因点是侧棱上一点，则，，因直线和平面所成角的大小为30°，则，解得，所以的值为.15．（大埔县虎山中学）如图，在四棱锥中，已知平面 ，且四边形为直角梯形，，，. （1）求平面与平面夹角的余弦值； （2）点是线段上的动点，当直线与所成的角最小时，求线段的长.【答案】（1）；（2）.【详解】解：（1）以为坐标原点，以，，所在直线分别为，，轴建立空间直角坐标系，则，，，1，，，2，0），，0，2），因为平面，所以是平面的一个法向量，，．，设平面的法向量为，，，则，取，得．故．又由图示得平面 PAB与平面 PCD 的夹角是锐角，所以平面 PAB与平面 PCD 夹角的余弦值是；，，，设，则，当且仅当，即时，取等号， 所以的最大值是，又因为在上单调递减， 与所成的角最小，， 所以线段BQ的长为.16．（天津市第七中学高三月考）如图，在四棱锥中，底面，，，，，点为棱的中点.（1）证明：：（2）求直线与平面所成角的正弦值：（3）若为棱上一点，且满足，求二面角的余弦值.【答案】（1）证明见解析；（2）；（3）.【详解】（1）以点A为原点，分别为轴，轴，轴，建立空间直角坐标系.可得，，，，由E为棱PC的中点，得，向量，，故，所以.（2）向量，，.设为平面PBD的法向量，则，即，令，得为平面PBD的一个法向量，所以，所以直线BE与平面PBD所成角的正弦值为.（3）向量，，，.因为点F在棱PC上，，，所以，由，得，因此，解得，即，设为平面FAB的法向量，则，即令，得为平面FAB的一个法向量.取平面ABP的法向量，则，经观察知二面角是锐角，所以其余弦值为.