专题 08 平面直角坐标系，函数基础知识与几何图形初步-2023年中考数学分项汇编（全国通用）

这是一份专题 08 平面直角坐标系，函数基础知识与几何图形初步-2023年中考数学分项汇编（全国通用），共39页。试卷主要包含了在平面直角坐标系中，点位于等内容，欢迎下载使用。
专题 08 平面直角坐标系，函数基础知识与几何图形初步
-2023年中考数学分项汇编（全国通用）
一．选择题（共25小题）
1．（2023•丽水）在平面直角坐标系中，点位于　　
A．第一象限 B．第二象限 C．第三象限 D．第四象限
2．（2023•台湾）如图，坐标平面上直线的方程式为，直线的方程式为，点的坐标为．根据图中点位置判断，下列关系何者正确　　

A．， B．， C．， D．，
3．（2023•台州）如图是中国象棋棋盘的一部分，建立如图所示的平面直角坐标系，已知“車”所在位置的坐标为，则“炮”所在位置的坐标为　　

A． B． C． D．
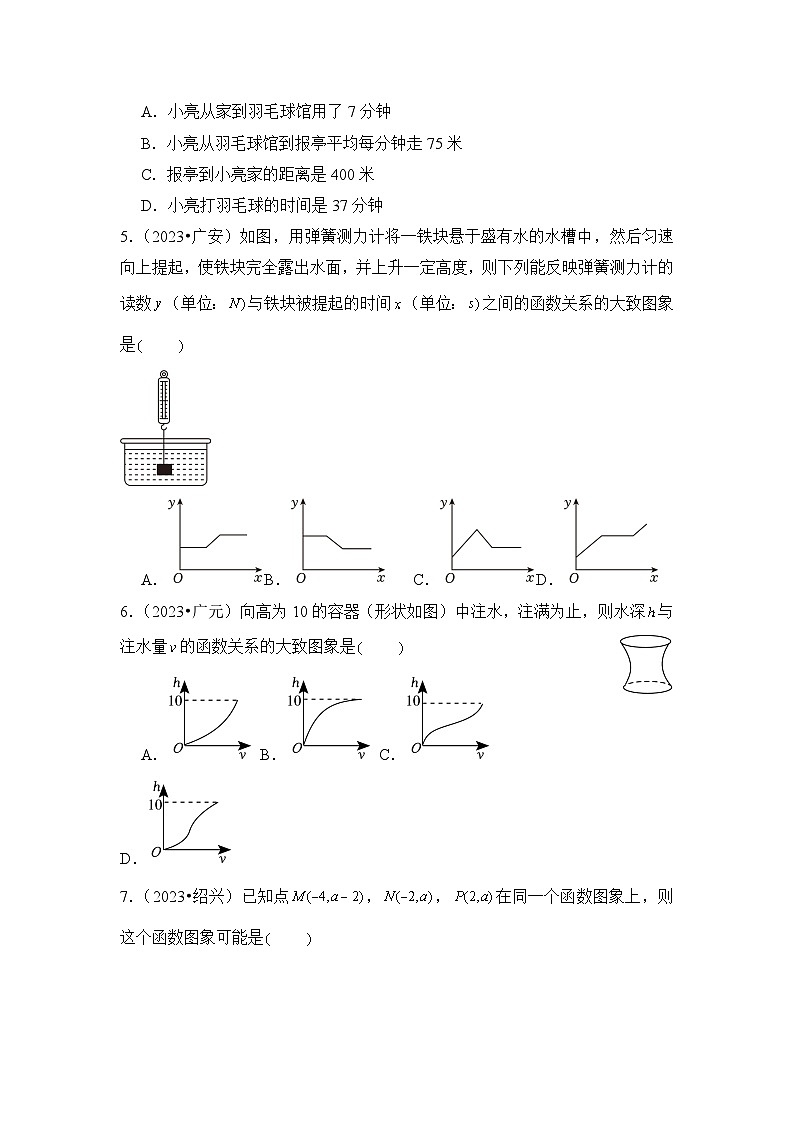
4．（2023•自贡）如图1，小亮家、报亭、羽毛球馆在一条直线上．小亮从家跑步到羽毛球馆打羽毛球，再去报亭看报，最后散步回家．小亮离家距离与时间之间的关系如图2所示．下列结论错误的是　　

A．小亮从家到羽毛球馆用了7分钟
B．小亮从羽毛球馆到报亭平均每分钟走75米
C．报亭到小亮家的距离是400米
D．小亮打羽毛球的时间是37分钟
5．（2023•广安）如图，用弹簧测力计将一铁块悬于盛有水的水槽中，然后匀速向上提起，使铁块完全露出水面，并上升一定高度，则下列能反映弹簧测力计的读数（单位：与铁块被提起的时间（单位：之间的函数关系的大致图象是　　

A．B． C．D．
6．（2023•广元）向高为10的容器（形状如图）中注水，注满为止，则水深与注水量的函数关系的大致图象是　　
A． B． C． D．
7．（2023•绍兴）已知点，，在同一个函数图象上，则这个函数图象可能是　　
A．B．C．D．
8．（2023•绥化）如图，在菱形中，，，动点，同时从点出发，点以每秒2个单位长度沿折线向终点运动；点以每秒1个单位长度沿线段向终点运动，当其中一点运动至终点时，另一点随之停止运动．设运动时间为秒，的面积为个平方单位，则下列正确表示与函数关系的图象是　　

A．B．C．D．
9．（2023•齐齐哈尔）如图，在正方形中，，动点，分别从点，同时出发，沿射线，射线的方向匀速运动，且速度的大小相等，连接，，．设点
运动的路程为，的面积为，下列图象中能反映与之间函数关系的是　　


A．B．C．D．
10．（2023•温州）【素材1】某景区游览路线及方向如图1所示，①④⑥各路段路程相等，⑤⑦⑧各路段路程相等，②③两路段路程相等．
【素材2】设游玩行走速度恒定，经过每个景点都停留20分钟，小温游路线①④⑤⑥⑦⑧用时3小时25分钟；小州游路线①②⑧，他离入口的路程与时间的关系（部分数据）如图2所示，在2100米处，他到出口还要走10分钟．
【问题】路线①③⑥⑦⑧各路段路程之和为　　

A．4200米 B．4800米 C．5200米 D．5400米
11．（2023•河北）如图是一种轨道示意图，其中和均为半圆，点，，，依次在同一直线上，且．现有两个机器人（看成点）分别从，两点同时出发，沿着轨道以大小相同的速度匀速移动，其路线分别为和．若移动时间为，两个机器人之间距离为．则与关系的图象大致是　　

A．B． C．D．
12．（2023•滨州）由化学知识可知，用表示溶液酸碱性的强弱程度，当时溶液呈碱性，当时溶液呈酸性，若将给定的溶液加水稀释，那么在下列图象中，能大致反映溶液的与所加水的体积之间对应关系的是　　
A．B． C．D．
13．（2023•浙江）如图是底部放有一个实心铁球的长方体水槽轴截面示意图，现向水槽匀速注水，下列图象中能大致反映水槽中水的深度与注水时间关系的是　　

A．B． C．D．
14．（2023•金昌）如图1，正方形的边长为4，为边的中点．动点从点出发沿匀速运动，运动到点时停止．设点的运动路程为，线段的长为，与的函数图象如图2所示，则点的坐标为　　

A．， B． C．， D．
15．（2023•遂宁）如图，在中，，，，点为线段上的动点．以每秒1个单位长度的速度从点向点移动，到达点时停止．过点作于点．作于点，连结，线段的长度与点的运动时间（秒的函数关系如图所示，则函数图象最低点的坐标为　　

A． B． C．， D．，
16．（2023•临沂）如图中用量角器测得的度数是　　

A． B． C． D．
17．（2023•巴中）某同学学习了正方体的表面展开图后，在如图所示的正方体的表面展开图上写下了“传承红色文化”六个字，还原成正方体后，“红”的对面是　　

A．传 B．承 C．文 D．化
18．（2023•连云港）如图，甲是由一条直径、一条弦及一段圆弧所围成的图形；乙是由两条半径与一段圆弧所围成的图形；丙是由不过圆心的两条线段与一段圆弧所围成的图形．下列叙述正确的是　　

A．只有甲是扇形 B．只有乙是扇形
C．只有丙是扇形 D．只有乙、丙是扇形
19．（2023•扬州）下列图形是棱锥侧面展开图的是　　
A．B． C．D．
20．（2023•达州）下列图形中，是长方体表面展开图的是　　
A．B．C．D．
21．（2023•宜昌）“争创全国文明典范城市，让文明成为宜昌人民的内在气质和城市的亮丽名片”．如图，是一个正方体的平面展开图，把展开图折叠成正方体后，“城”字对面的字是　　

A．文 B．明 C．典 D．范
22．（2023•乐山）下面几何体中，是圆柱的为　　
A．B． C．D．
23．（2023•巴中）如图所示图形中为圆柱的是　　
A．B． C．D．
24．（2023•河北）淇淇一家要到革命圣地西柏坡参观．如图，西柏坡位于淇淇家南偏西的方向，则淇淇家位于西柏坡的　　

A．南偏西方向 B．南偏东方向
C．北偏西方向 D．北偏东方向
25．（2023•台湾）如图，直角柱的底面为直角三角形，若，，则连接后，下列叙述何者正确　　

A．， B．，
C．， D．，
二．填空题（共13小题）
26．（2023•岳阳）在平面直角坐标系中，点所在象限是第 　　象限．
27．（2023•巴中）已知为正整数，点在第一象限中，则　　．
28．（2023•大连）如图，在数轴上，，过作直线于点，在直线上截取，且在上方．连接，以点为圆心，为半径作弧交直线于点，则点的横坐标为 　　．

29．（2023•连云港）画一条水平数轴，以原点为圆心，过数轴上的每一刻度点画同心圆，过原点按逆时针方向依次画出与正半轴的角度分别为、、、、、的射线，这样就建立了“圆”坐标系．如图，在建立的“圆”坐标系内，我们可以将点、、的坐标分别表示为、、，则点的坐标可以表示为 　　．

30．（2023•黑龙江）在函数中，自变量的取值范围是　　．
31．（2023•齐齐哈尔）在函数 中，自变量的取值范围是 　　．
32．（2023•云南）函数的自变量的取值范围是 　　．
33．（2023•达州）函数的自变量的取值范围是 　　．
34．（2023•岳阳）函数中，自变量的取值范围是 　　．
35．（2023•广安）函数的自变量的取值范围是 　　．
36．（2023•临沂）小明利用学习函数获得的经验研究函数的性质，得到如下结论：
①当时，越小，函数值越小；
②当时，越大，函数值越小；
③当时，越小，函数值越大；
④当时，越大，函数值越大．
其中正确的是 　　（只填写序号）．
37．（2023•烟台）如图1，在中，动点从点出发沿折线匀速运动至点后停止．设点的运动路程为，线段的长度为，图2是与的函数关系的大致图象，其中点为曲线的最低点，则的高的长为 　　．

38．（2023•乐山）如图，点在直线上，是的平分线，若，则的度数为 　　．

三．解答题（共1小题）
39．（2023•永州）小明观察到一个水龙头因损坏而不断地向外滴水，为探究其漏水造成的浪费情况，小明用一个带有刻度的量筒放在水龙头下面装水，每隔一分钟记录量筒中的总水量，但由于操作延误，开始计时的时候量筒中已经有少量水，因而得到如表的一组数据：
时间
（单位：分钟）
1
2
3
4
5

总水量
（单位：毫升）
7
12
17
22
27

（1）探究：根据上表中的数据，请判断和，为常数）哪一个能正确反映总水量与时间的函数关系？并求出关于的表达式；
（2）应用：
①请你估算小明在第20分钟测量时量筒的总水量是多少毫升？
②一个人一天大约饮用1500毫升水，请你估算这个水龙头一个月（按30天计）的漏水量可供一人饮用多少天．

参考答案
一．选择题（共25小题）
1．（2023•丽水）在平面直角坐标系中，点位于　　
A．第一象限 B．第二象限 C．第三象限 D．第四象限
【分析】依据，即可得出点在第二象限．
【解答】解：，
点在第二象限．
故选：．
【点评】本题考查了各象限内点的坐标的符号特征和平方的非负性，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限；第二象限；第三象限；第四象限．
2．（2023•台湾）如图，坐标平面上直线的方程式为，直线的方程式为，点的坐标为．根据图中点位置判断，下列关系何者正确　　

A．， B．， C．， D．，
【分析】利用直角坐标系中点的坐标的特点，图形的性质解答．
【解答】解：坐标平面上直线的方程式为，直线的方程式为，
直线与直线交点的坐标为，
点的坐标为，
根据图中点位置得，．
故选：．
【点评】本题考查了坐标与图形性质，解题的关键是熟练掌握直角坐标系中点的坐标的特点．
3．（2023•台州）如图是中国象棋棋盘的一部分，建立如图所示的平面直角坐标系，已知“車”所在位置的坐标为，则“炮”所在位置的坐标为　　

A． B． C． D．
【分析】直接利用“車”位于点，得出原点的位置，进而得出答案．
【解答】解：如图所示：“炮”所在位置的坐标为：．
故选：．
【点评】此题主要考查了坐标确定位置，正确得出原点的位置是解题关键．
4．（2023•自贡）如图1，小亮家、报亭、羽毛球馆在一条直线上．小亮从家跑步到羽毛球馆打羽毛球，再去报亭看报，最后散步回家．小亮离家距离与时间之间的关系如图2所示．下列结论错误的是　　

A．小亮从家到羽毛球馆用了7分钟
B．小亮从羽毛球馆到报亭平均每分钟走75米
C．报亭到小亮家的距离是400米
D．小亮打羽毛球的时间是37分钟
【分析】根据图象逐个分析即可．
【解答】解：、由图象得：小亮从家到羽毛球馆用了7分钟，故选项不符合题意；
、由图象可知：小亮从羽毛球馆到报亭的平均速度为：（千米分）（米分），故选项不符合题意；
、由图象知报亭到小亮家的距离是0.4千米，即400米，故选项不符合题意；
、由图象知小亮打羽毛球的时间是（分钟），故选项符合题意；
故选：．
【点评】本题考查了函数图象，观察图象，从图象中获取信息是解题的关键．
5．（2023•广安）如图，用弹簧测力计将一铁块悬于盛有水的水槽中，然后匀速向上提起，使铁块完全露出水面，并上升一定高度，则下列能反映弹簧测力计的读数（单位：与铁块被提起的时间（单位：之间的函数关系的大致图象是　　

A． B．
C． D．
【分析】根据题意可将铁块被拉起的过程分为三段：当铁块露出水面之前，根据分析得出弹簧测力计的读数不变；当铁块逐渐露出水面的过程中，根据分析得弹簧测力计的读数逐渐增大；当铁块完全露出水面之后，根据分析得弹簧测力计的读数不变．以此即可判断函数图象．
【解答】解：根据浮力的知识可知，当铁块露出水面之前，，
此过程浮力不变，铁块的重力不变，故拉力不变，即弹簧测力计的读数不变；
当铁块逐渐露出水面的过程中，，
此过程浮力逐渐减小，铁块重力不变，故拉力逐渐增大，即弹簧测力计的读数逐渐增大；
当铁块完全露出水面之后，，
此过程拉力等于铁块重力，即弹簧测力计的读数不变．
综上，弹簧测力计的读数先不变，再逐渐增大，最后不变．
故选：．
【点评】本题主要考查函数的图象，涉及与浮力有关物理知识，利用分类讨论思想分析得出不同过程中弹簧测力计读数的变化情况是解题关键．
6．（2023•广元）向高为10的容器（形状如图）中注水，注满为止，则水深与注水量的函数关系的大致图象是　　

A． B．
C． D．
【分析】依据题意，从水瓶的构造形状上看，从底部到顶部的变化关系为：开始宽，逐渐细小，再变宽，再从函数的图象上看，即可得解．
【解答】解：依据题意，从水瓶的构造形状上看，从底部到顶部的变化关系为：开始宽，逐渐细小，再变宽．
则注入的水量随水深的变化关系为：先慢再快，最后又变慢．
那么从函数的图象上看，
对应的图象变化为先快再慢，最后又变快，不符合．
、对应的图象中间没有变化，只有符合条件．
故选：．
【点评】本题主要考查函数的定义及函数的图象的关系，抓住变量之间的变化关系是解题的关键．
7．（2023•绍兴）已知点，，在同一个函数图象上，则这个函数图象可能是　　
A． B．
C． D．
【分析】由点，关于轴对称，可排除选项、，再根据，，可知在轴的左侧，随的增大而增大，从而排除选项．
【解答】解：由，在同一个函数图象上，可知图象关于轴对称，故选项、不符合题意；
由，，可知在轴的左侧，随的增大而增大，故选项符合题意；
故选：．
【点评】此题考查了函数的图象．注意掌握排除法在选择题中的应用是解此题的关键．
8．（2023•绥化）如图，在菱形中，，，动点，同时从点出发，点以每秒2个单位长度沿折线向终点运动；点以每秒1个单位长度沿线段向终点运动，当其中一点运动至终点时，另一点随之停止运动．设运动时间为秒，的面积为个平方单位，则下列正确表示与函数关系的图象是　　

A． B．
C． D．
【分析】连接，过作于，根据已知条件得到是等边三角形，根据相似三角形的判定定理得到，根据相似三角形的性质得到，当时，点在上，当时，点在上，根据三角形的面积公式即可得到结论．
【解答】解：连接，过作于，当时，点在上，

在菱形中，，，
，
是等边三角形，
，，
，小，
，
，
，
，
，
，
当时，点在上，

，
综上所述，当时的函数图象是开口向上的抛物线的一部分，当时，函数图象是直线的一部分，
故选：．
【点评】本题考查了动点问题的函数图象，二次函数的图象，一次函数的图象，矩形的性质，勾股定理，等边三角形的判定和性质，相似三角形的判定和性质，熟练掌握各定理是解题的关键．
9．（2023•齐齐哈尔）如图，在正方形中，，动点，分别从点，同时出发，沿射线，射线的方向匀速运动，且速度的大小相等，连接，，．设点
运动的路程为，的面积为，下列图象中能反映与之间函数关系的是　　


A． B．
C． D．
【分析】根据点的运动情况，写出每种情况和之间的函数关系式，即可确定图象．
【解答】解：时，在上，在上，依题意可知：
设，
，


；
该二次函数图象开口向上，
当时，二次函数的最小值为6；
当或4时，二次函数的最大值为8；
故选：．
【点评】本题是运动型综合题，考查了动点问题的函数图象、正方形的性质、三角形的面积等知识点解题关键是深刻理解动点的函数图象，了解图象中关键点所代表的实际意义，理解动点的完整运动过程．
10．（2023•温州）【素材1】某景区游览路线及方向如图1所示，①④⑥各路段路程相等，⑤⑦⑧各路段路程相等，②③两路段路程相等．
【素材2】设游玩行走速度恒定，经过每个景点都停留20分钟，小温游路线①④⑤⑥⑦⑧用时3小时25分钟；小州游路线①②⑧，他离入口的路程与时间的关系（部分数据）如图2所示，在2100米处，他到出口还要走10分钟．
【问题】路线①③⑥⑦⑧各路段路程之和为　　

A．4200米 B．4800米 C．5200米 D．5400米
【分析】设①④⑥各路段路程为米，⑤⑦⑧各路段路程为米，②③各路段路程为米，由题意及图象可知，然后根据“游玩行走速度恒定，经过每个景点都停留20分钟，小温游路线①④⑤⑥⑦⑧用时3小时25分钟”可进行求解．
【解答】解：由图象可知：小州游玩行走的时间为（分钟），
小温游玩行走的时间大（分钟），
设①④⑥各路段路程为米，⑤⑦⑧各路段路程为米，②③各路段路程为米
由图象可得：，
解得：，
游玩行走的速度为： （米秒），
由于游玩行走速度恒定，则小温游路线①④⑤⑥⑦⑧的路程为：，
，
路线①③⑥⑦⑧各路段路程之和为：（米．
故选：．
【点评】本题主要考查三元一次方程组的应用及函数图象，解题的关键是理解题中所给信息，找到它们之间的等量关系．
11．（2023•河北）如图是一种轨道示意图，其中和均为半圆，点，，，依次在同一直线上，且．现有两个机器人（看成点）分别从，两点同时出发，沿着轨道以大小相同的速度匀速移动，其路线分别为和．若移动时间为，两个机器人之间距离为．则与关系的图象大致是　　

A． B．
C． D．
【分析】设圆的半径为，根据机器人移动时最开始的距离为，之后同时到达点，两个机器人之间的距离越来越小，当两个机器人分别沿和移动时，此时两个机器人之间的距离是半径，当机器人分别沿和移动时，此时两个机器人之间的距离越来越大，据此得出结论即可．
【解答】解：由题意可得：机器人（看成点）分别从，两点同时出发，设圆的半径为，
两个机器人最初的距离是，
两个人机器人速度相同，
同时到达点，，
两个机器人之间的距离越来越小，故排除、；
当两个机器人分别沿和移动时，此时两个机器人之间的距离是半径，保持不变，
当机器人分别沿和移动时，此时两个机器人之间的距离越来越大，故排除；
故选：．
【点评】本题考查动点函数图象，找到运动时的特殊点用排除法是关键．
12．（2023•滨州）由化学知识可知，用表示溶液酸碱性的强弱程度，当时溶液呈碱性，当时溶液呈酸性，若将给定的溶液加水稀释，那么在下列图象中，能大致反映溶液的与所加水的体积之间对应关系的是　　
A． B．
C． D．
【分析】根据化学知识和函数图象的知识，分析几个选项即可．
【解答】解：根据题意：将给定的溶液加水稀释，那么开始，随着慢慢加水，溶液碱性越来越弱，值逐渐减小．故选：．
【点评】本题属于数学与化学知识相结合的题型，难度不大，认真分析图形即可．
13．（2023•浙江）如图是底部放有一个实心铁球的长方体水槽轴截面示意图，现向水槽匀速注水，下列图象中能大致反映水槽中水的深度与注水时间关系的是　　

A． B．
C． D．
【分析】根据题意可分两段进行分析：当水的深度未超过球顶时；当水的深度超过球顶时．分别分析出水槽中装水部分的宽度变化情况，进而判断出水的深度变化快慢，以此得出答案．
【解答】解：当水的深度未超过球顶时，
水槽中能装水的部分的宽度由下到上由宽逐渐变窄，再变宽，
所以在匀速注水过程中，水的深度变化先从上升较慢变为较快，再变为较慢；
当水的深度超过球顶时，
水槽中能装水的部分宽度不再变化，
所以在匀速注水过程中，水的深度的上升速度不会发生变化．
综上，水的深度先上升较慢，再变快，然后变慢，最后匀速上升．
故选：．
【点评】本题主要考查函数的图象，利用分类讨论思想，根据不同时间段能装水部分的宽度的变化情况分析水的深度变化情况是解题关键．
14．（2023•金昌）如图1，正方形的边长为4，为边的中点．动点从点出发沿匀速运动，运动到点时停止．设点的运动路程为，线段的长为，与的函数图象如图2所示，则点的坐标为　　

A．， B． C．， D．
【分析】根据图2确定点的横坐标为的长度，纵坐标为的长度，然后求值即可．
【解答】解：由题意可知，当点在边上时，的值先减小后增大，
当点在边上时，的值逐渐减小，
点的横坐标为的长度，纵坐标为的长度，
，，
，
，，
故选：．
【点评】本题考查动点问题的函数图象，关键是根据图2确定点的坐标与正方形的边之间的关系．
15．（2023•遂宁）如图，在中，，，，点为线段上的动点．以每秒1个单位长度的速度从点向点移动，到达点时停止．过点作于点．作于点，连结，线段的长度与点的运动时间（秒的函数关系如图所示，则函数图象最低点的坐标为　　

A． B． C．， D．，
【分析】根据矩形的性质和直角三角形的性质，可以得到时，取得最小值，此时取得最小值，然后即可求得点的坐标．
【解答】解：连接，
，，，
，
是直角三角形，，
，，
，
，
四边形是矩形，
，
当时，取得最小值，此时，，
函数图象最低点的坐标为，，
故选：．

【点评】本题考查动点问题的函数图象，解答本题的关键是明确题意，利用数形结合的思想解答．
16．（2023•临沂）如图中用量角器测得的度数是　　

A． B． C． D．
【分析】本题根据的位置和量角器的使用方法可得出答案．
【解答】解：根据起始位置，另一条边可得：．
故选：．
【点评】本题主要考查了学生量角器的使用方法，结合的位置进行思考是解题关键．
17．（2023•巴中）某同学学习了正方体的表面展开图后，在如图所示的正方体的表面展开图上写下了“传承红色文化”六个字，还原成正方体后，“红”的对面是　　

A．传 B．承 C．文 D．化
【分析】根据正方体的平面展开图的特点，相对的两个面中间一定隔着一个小正方形，且没有公共的顶点，结合展开图很容易找到与“红”字所在面相对的面上的汉字．
【解答】解：根据图示知：“传”与“文”相对；
“承”与“色”相对；
“红”与“化”相对．
故选：．
【点评】本题考查灵活运用正方体的相对面解答问题，解决本题的关键是根据正方体的平面展开图的特点，相对的两个面中间一定隔着一个小正方形，且没有公共的顶点．
18．（2023•连云港）如图，甲是由一条直径、一条弦及一段圆弧所围成的图形；乙是由两条半径与一段圆弧所围成的图形；丙是由不过圆心的两条线段与一段圆弧所围成的图形．下列叙述正确的是　　

A．只有甲是扇形 B．只有乙是扇形
C．只有丙是扇形 D．只有乙、丙是扇形
【分析】根据扇形的定义进行判断．
【解答】解：由扇形的定义可知，只有乙是扇形，
故选：．
【点评】本题主要考查了认识平面图形—扇形，应熟知扇形的定义：由圆心角的两条半径和圆心角所对的圆弧围成的图形叫做扇形．
19．（2023•扬州）下列图形是棱锥侧面展开图的是　　
A． B．
C． D．
【分析】由棱锥的侧面展开图的特征可知答案．
【解答】解：四棱锥的侧面展开图是四个三角形．
故选：．
【点评】本题考查了几何体的展开图，熟记常见立体图形的侧面展开图和侧面的特征是解决此类问题的关键．
20．（2023•达州）下列图形中，是长方体表面展开图的是　　
A． B．
C． D．
【分析】根据长方体的展开图得出结论即可．
【解答】解：由题意知，图形可以折叠成长方体，
故选：．
【点评】本题主要考查长方体的展开图，熟练掌握长方体的展开图是解题的关键．
21．（2023•宜昌）“争创全国文明典范城市，让文明成为宜昌人民的内在气质和城市的亮丽名片”．如图，是一个正方体的平面展开图，把展开图折叠成正方体后，“城”字对面的字是　　

A．文 B．明 C．典 D．范
【分析】根据正方体的平面展开图的特点，相对的两个面中间一定隔着一个小正方形，且没有公共边和公共顶点，即“对面无临点”，依此来找相对面．
【解答】解：正方体的表面展开图，相对的面之间一定隔着一个小正方形，且没有公共边和公共顶点，
“城”字对面的字是“明”．
故选：．
【点评】本题主要考查了正方体相对两个面上的文字，熟练掌握正方体的表面展开图的特点是解题的关键．
22．（2023•乐山）下面几何体中，是圆柱的为　　
A． B．
C． D．
【分析】根据各个选项中的几何体的形体特征进行判断即可．
【解答】解：．选项中的几何体是圆锥体，因此选项不符合题意；
．选项中的几何体是球体，因此选项不符合题意；
．选项中的几何体是圆柱体，因此选项符合题意；
．选项中的几何体是四棱柱，因此选项不符合题意；
故选：．
【点评】本题考查认识立体图形，掌握圆柱体，圆锥体，棱柱，球的形体特征是正确判断的前提．
23．（2023•巴中）如图所示图形中为圆柱的是　　
A． B．
C． D．
【分析】根据圆柱的特点进行判断即可．
【解答】解：由圆柱的特征可知，选项是圆柱．
故选：．
【点评】本题主要考查的是认识立体图形，认识常见几何图形是解题的关键．
24．（2023•河北）淇淇一家要到革命圣地西柏坡参观．如图，西柏坡位于淇淇家南偏西的方向，则淇淇家位于西柏坡的　　

A．南偏西方向 B．南偏东方向
C．北偏西方向 D．北偏东方向
【分析】根据题意可得：，，然后利用平行线的性质可得，从而根据方向角的定义，即可解答．
【解答】解：如图：

由题意得：，，
，
淇淇家位于西柏坡的北偏东方向，
故选：．
【点评】本题考查了方向角的定义，熟练掌握方向角的定义是解题的关键．
25．（2023•台湾）如图，直角柱的底面为直角三角形，若，，则连接后，下列叙述何者正确　　

A．， B．，
C．， D．，
【分析】根据直棱柱的性质得，再根据三角形的边角关系即可得出答案．
【解答】解：如图，连接，

，，
，
，
，
在和中，，，，
，
故选：．
【点评】本题考查了认识立体图形，关键是掌握直棱柱的性质和三角形的边角关系．
二．填空题（共13小题）
26．（2023•岳阳）在平面直角坐标系中，点所在象限是第 　三　象限．
【分析】根据第一象限；第二象限；第三象限；第四象限，可得答案．
【解答】解：点在第三象限，
故答案为：三．
【点评】此题主要考查了点的坐标，关键是掌握四个象限内点的坐标符号．
27．（2023•巴中）已知为正整数，点在第一象限中，则　1　．
【分析】根据平面直角坐标系中第一象限内的点的横、纵坐标都为正数，得到，即可求出的取值范围，再根据为正整数即可得到的值．
【解答】解：点在第一象限，
，
，
又为正整数，
．
故答案为：1．
【点评】本题主要考查了平面直角坐标系中点的坐标特征，熟知：第一象限内的点的坐标特征是，第二象限内的点的坐标特征是，第三象限内的点的坐标特征是，第四象限内的点的坐标特征是．
28．（2023•大连）如图，在数轴上，，过作直线于点，在直线上截取，且在上方．连接，以点为圆心，为半径作弧交直线于点，则点的横坐标为 　　．

【分析】在中，利用勾股定理求出，则，进而求得，据此即可求解．
【解答】解：，
，
在中，，
以点为圆心，为半径作弧交直线于点，
，
，
点的横坐标为．
故答案为：，
【点评】本题主要考查勾股定理，实数与数轴，利用勾股定理正确求出的长是解题关键．
29．（2023•连云港）画一条水平数轴，以原点为圆心，过数轴上的每一刻度点画同心圆，过原点按逆时针方向依次画出与正半轴的角度分别为、、、、、的射线，这样就建立了“圆”坐标系．如图，在建立的“圆”坐标系内，我们可以将点、、的坐标分别表示为、、，则点的坐标可以表示为 　　．

【分析】在该坐标系中，某点的坐标用两个参数来描述：一个是该点与原点的距离，另一个是原点与该点所在的射线与轴正半轴之间的夹角．
【解答】解：点与圆心的距离为3，射线与轴正方向之间的夹角为，
点的坐标为．
故答案为：．
【点评】该题较简单，主要考查在不同坐标系中点的表示方法．
30．（2023•黑龙江）在函数中，自变量的取值范围是　　．
【分析】因为二次根式的被开方数要为非负数，即，解此不等式即可．
【解答】解：根据题意得：，解得：．
故答案为：．
【点评】当函数表达式是二次根式时，被开方数为非负数．
31．（2023•齐齐哈尔）在函数 中，自变量的取值范围是 　且　．
【分析】根据二次根式有意义的条件及分母不能为0即可求得答案．
【解答】解：已知函数为，
则，且，
解得：且，
故答案为：且．
【点评】本题考查求函数自变量的取值范围，根据二次根式有意义的条件及分母不能为0求得，且是解题的关键．
32．（2023•云南）函数的自变量的取值范围是 　　．
【分析】根据分式的分母不能为0即可求得答案．
【解答】解：已知函数为，
则
即，
故答案为：．
【点评】本题考查函数自变量的取值范围，此为基础且重要知识点，必须熟练掌握．
33．（2023•达州）函数的自变量的取值范围是 　　．
【分析】由二次根式的被开方数大于等于0可得，由分式有意义的性质可得，即可求出自变量的取值范围．
【解答】解：根据题意得：且，
即，
解得：．
故答案为：．
【点评】考查了函数自变量的范围，函数自变量的范围一般从三个方面考虑：
（1）当函数表达式是整式时，自变量可取全体实数；
（2）当函数表达式是分式时，考虑分式的分母不能为0；
（3）当函数表达式是二次根式时，被开方数非负．
34．（2023•岳阳）函数中，自变量的取值范围是 　　．
【分析】根据分母不为0可得：，然后进行计算即可解答．
【解答】解：由题意得：，
解得：，
故答案为：．
【点评】本题考查了函数自变量的取值范围，熟练掌握分母不为0是解题的关键．
35．（2023•广安）函数的自变量的取值范围是 　且　．
【分析】根据二次根式的性质和分式的意义，被开方数大于等于0，分母不等于0，就可以求解
【解答】解：根据题意得：，
解得：且．
故答案为：且．
【点评】本题考查的知识点为：分式有意义，分母不为0；二次根式的被开方数是非负数．
36．（2023•临沂）小明利用学习函数获得的经验研究函数的性质，得到如下结论：
①当时，越小，函数值越小；
②当时，越大，函数值越小；
③当时，越小，函数值越大；
④当时，越大，函数值越大．
其中正确的是 　②③④　（只填写序号）．
【分析】由题意，利用图象法作答，可以得解．
【解答】解：如图所示，

当时，越小，函数值越大，故①错误．
当时，越大，函数值越小，故②正确．
当时，越小，函数值越大，故③正确．
当时，越大，函数值越大，故④正确．
故答案为：②③④．
【点评】本题考查了探究函数的增减性问题，解题时需要灵活运用方法是关键．
37．（2023•烟台）如图1，在中，动点从点出发沿折线匀速运动至点后停止．设点的运动路程为，线段的长度为，图2是与的函数关系的大致图象，其中点为曲线的最低点，则的高的长为 　　．

【分析】过点作于点，当点与重合时，在图2中点表示当时，点到达点，此时当在上运动时，最小，勾股定理求得．然后等面积法即可求解．
【解答】解：如图过点作于点，当点与重合时，在图2中点表示当时，点到达点，此时当在上运动时，最小，

，，，
在中，，，
，
，
．
故答案为：．
【点评】本题考查了动点问题的函数图象，勾股定理，垂线段最短，从函数图象获取信息是解题的关键．
38．（2023•乐山）如图，点在直线上，是的平分线，若，则的度数为 　　．

【分析】根据邻补角定义求得的度数，再根据角平分线定义即可求得答案．
【解答】解：，
，
是的平分线，
，
故答案为：．
【点评】本题主要考查角平分线的定义，此为几何中基础且重要知识点，必须熟练掌握．
三．解答题（共1小题）
39．（2023•永州）小明观察到一个水龙头因损坏而不断地向外滴水，为探究其漏水造成的浪费情况，小明用一个带有刻度的量筒放在水龙头下面装水，每隔一分钟记录量筒中的总水量，但由于操作延误，开始计时的时候量筒中已经有少量水，因而得到如表的一组数据：
时间
（单位：分钟）
1
2
3
4
5

总水量
（单位：毫升）
7
12
17
22
27

（1）探究：根据上表中的数据，请判断和，为常数）哪一个能正确反映总水量与时间的函数关系？并求出关于的表达式；
（2）应用：
①请你估算小明在第20分钟测量时量筒的总水量是多少毫升？
②一个人一天大约饮用1500毫升水，请你估算这个水龙头一个月（按30天计）的漏水量可供一人饮用多少天．
【分析】（1）根据上表中的数据，可知与成一次函数关系，根据点的坐标利用待定系数法即可求出该函数关系式；
（2）①当时，求出的值即可；
②当分钟时，求出的值，即可求出答案．
【解答】解：（1）根据上表中的数据，，为常数）能正确反映总水量与时间的函数关系，
当时，，当时，，
，
，
；
（2）①当时，，
即估算小明在第20分钟测量时量筒的总水量是102毫升；
②当分钟时，（毫升），
当时，，
（天，
答：估算这个水龙头一个月（按30天计）的漏水量可供一人饮用144天．
【点评】本题考查一次函数的应用，解答本题的关键是明确题意，利用一次函数的性质解答．