湖南省怀化市通道县2022-2023学年八年级下学期期中考试数学试卷(含解析)

2023年上期八年级期中考试卷

数   学（第1—2章)

一、选择题

1．直角三角形的一锐角是，那么另一锐角是（       ）

A． B． C． D．

2．十边形的内角和是（       ）

A．1440° B．1260° C．1080°                     D．900°

3．如图，小明和小华同时从P处分别向北偏东60°和南偏东30°方向出发，他们的速度分别是3m/s和4m/s，则10s后他们之间的距离为（　　）

A．30m B．40m C．50m D．60m

4．下列图形中，既是轴对称图形又是中心对称图形的是（        ）

A． B． C． D．

5．两个直角三角形中：①一锐角和斜边对应相等；②斜边和一直角边对应相等；③有两条边相等；④两个锐角对应相等．能使这两个直角三角形全等的是（       ）

A．①② B．②③ C．③④ D．①②③④

6．在中，，的平分线交于D，若，则点D到的距离是（       ）

A． B． C． D．

7．如图，公路、互相垂直，公路的中点M与点C被湖隔开，若测得的长为，则M、C两点间的距离为（　　）

A． B． C． D．

8．如图，菱形的对角线，，则该菱形的面积为（       ）．

A．60 B．80 C．100 D．120

9．下列命题中，真命题是（ ）．

A．对角线相等的四边形是矩形

B．对角线互相垂直的四边形是菱形

C．对角线互相平分的四边形是平行四边形

D．对角线互相垂直平分的四边形是正方形

10．如图，将矩形纸片折叠，使边落在对角线上，折痕为，且D点落在对角线处．若，，则的长为（       ）

A．4 B． C．5 D．6

二、填空题

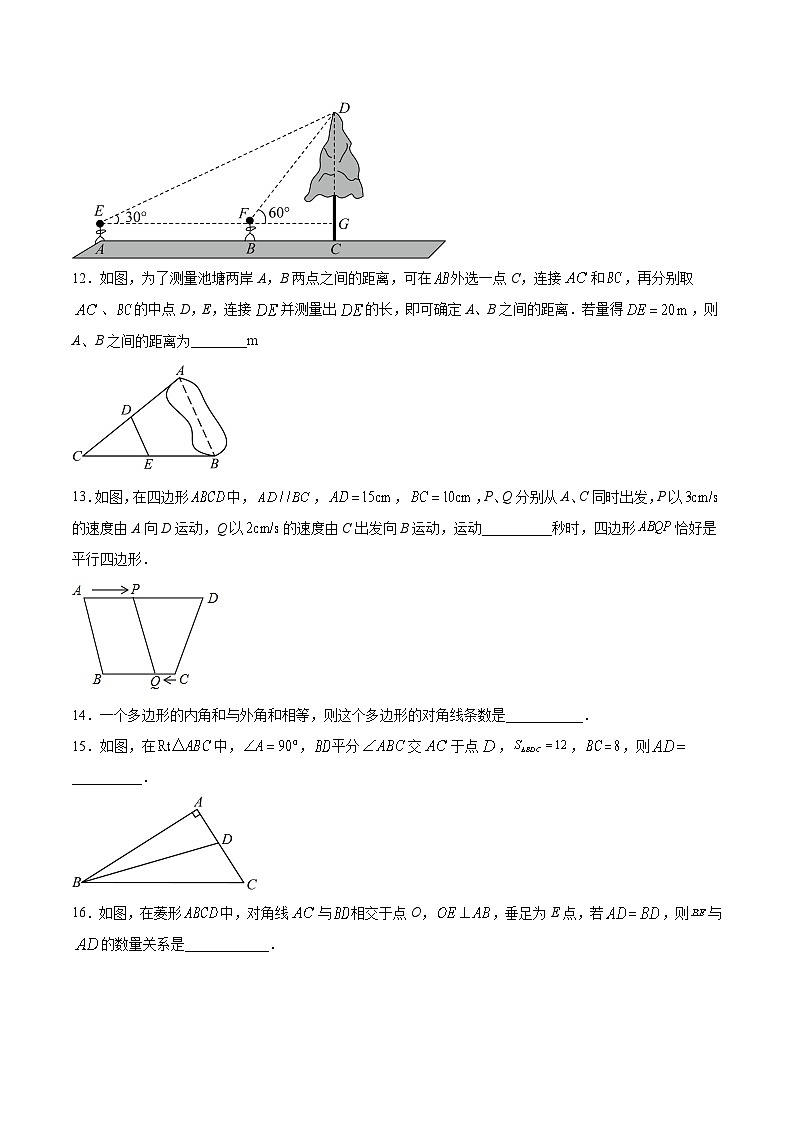
11．如图，树杆垂直于地面，为测树高，小明在A处，测得树顶D的仰角是，他沿方向走了20米，到达B处，测得树顶D的仰角是，小明的身高是1.6米，则树的高度是________．（，结果保留整数）

12．如图，为了测量池塘两岸A，B两点之间的距离，可在外选一点C，连接和，再分别取、的中点D，E，连接并测量出的长，即可确定A、B之间的距离．若量得，则A、B之间的距离为________m

13．如图，在四边形中，，，，P、Q分别从A、C同时出发，P以的速度由A向D运动，Q以的速度由C出发向B运动，运动__________秒时，四边形恰好是平行四边形．

14．一个多边形的内角和与外角和相等，则这个多边形的对角线条数是___________．

15．如图，在中，，平分交于点，，，则__________．

16．如图，在菱形中，对角线与相交于点O，，垂足为E点，若，则与的数量关系是____________．

三、解答题

17．如图，在平行四边形中，的平分线交于E，，求的度数

18．已知：如图，，为对角线上的两点，且．求证：四边形是平行四边形．

19．如图，在A岛周围25海里水域内有暗礁，一轮船由西向东航行到O处时，测得A岛在北偏东60°的方向，且与轮船相距海里.若该轮船继续保持由西向东的航向，那么有触礁的危险吗？请说明理由.（）

20．如图，D，E分别是，上的中点，F是上的一点，且，若，，求的长.

21．如图，B、F、C、E在同一条直线上，，，．求证：．

22．如图，E、F、G、H分别是任意平面四边形ABCD四边的中点

(1)求证：四边形EFGH是平行四边形；

(2)请给四边形ABCD添加一个条件，使得四边形EFGH是矩形．

23．分别以的边、为边，在的外部作正方形和正方形，连接、求证：

(1)

(2)

24．如图，在平行四边形中，，，过点A作边的垂线交的延长线于点E，点F是垂足，连接、，交于点O．求证

(1)四边形是正方形；

(2)；

(3).

答案

1．C

解：直角三角形的一锐角是，那么另一锐角是，

故选：C．

2．A

解：十边形的内角和： ；

故选：A．

3．C

解：根据题意得：，

，，

∴，

即10s后他们之间的距离为．

故选：C

4．B

解：A．不是轴对称图形，是中心对称图形，故本选项不符合题意；

B．既是轴对称图形，又是中心对称图形，故本选项符合题意；

C．是轴对称图形，不是中心对称图形，故本选项不符合题意；

D．是轴对称图形，不是中心对称图形，故本选项不符合题意；

故选：B．

5．A

解：①有斜边和一个锐角对应相等，可以利用AAS证明全等，故①正确；

②有斜边和一条直角边对应相等，可以利用HL证明全等，故②正确；

③有两条边相等，没有表明是对应边相等，不一定可以利用HL或SAS证明全等，故③错误；

④有两个锐角对应相等，不能利用AAA证明全等，故④错误；

综上分析可知①②正确，故A正确．

故选：A．

6．D

解：

解：∵，的平分线交于D，

∴，

∵，.

∴，即点D到的距离是，

故选：D．

7．A

解：∵公路、互相垂直，

∴，

∵M为的中点，

∴，

∵，

∴， 即M，C两点间的距离为，

故选：A．

8．A

解：菱形的对角线，，

该菱形的面积为：，

故选：A．

9．C

解：A、两条对角线相等且相互平分的四边形为矩形；故本选项错误；

B、对角线互相垂直的平行四边形是菱形；故本选项错误；

C、对角线互相平分的四边形是平行四边形；故本选项正确；

D、对角线互相垂直平分且相等的四边形是正方形；故本选项错误．

故选C．

10．B

解：在矩形中，，，

∴，

∴，

根据折叠可得：，

∴，，

设，则，，，

在中：， ，

解得：，

故选：B．

11．米##

解：根据题意可得：米，米，，，，

∴，

∴，

∴米，

，

∴米，

∴米，

∴（米）．

故答案为：19米．

12．

解：∵点D，E分别是，的中点，

∴是的中位线，而，

∴．

故答案为：40．

13．2

解：设x秒后，四边形ABQP是平行四边形，

∵P以3cm/s的速度由A向D运动，Q以2cm/s的速度由C出发向B运动，

∴AP=3xcm，CQ=2xcm，

∵BC=10cm，

∴QB=（10-2x）cm，

当AP=BQ时，四边形ABQP是平行四边形，

∴3x=10-2x， 解得：x=2．

故答案为：2．

14．2

设多边形的边数为n，

根据题意（n-2）•180°=360°，

解得n=4．

则四边形的对角线为，

故答案为：2．

15．3

解：过D点作，垂足为E，

由得，而，

解得，

∵平分，，，

∴．

故答案为 3．

16．

解：在菱形中，，，

，

是等边三角形，

，

，

∴，

∴，

故答案为：．

17．

解：∵四边形是平行四边形，

∴，

∴，

∵平分，

∴，

∴，

∵，

∴，

∴．

18．证明：∵四边形是平行四边形，

∴，，

∴，即，

又∵，

∴，

∴，

∴，，

∴，

∴，

∴四边形是平行四边形．

19．解：过点A作于点B，如图，

由题意得，，海里，

在中，（海里），

∵，，

∴没有触礁风险，

答：没有触礁风险．

20．解：∵D，E分别是，上的中点，，

∴是的中位线，

∴．

∵，D是的中点，，

∴，

∴．

21．证明：∵，

∴，

∴，

在和中，，

∴，

∴．

22．（1）解：如图，连接BD，

E、F、G、H分别是任意平面四边形ABCD四边的中点

四边形EFGH是平行四边形；

（2）加上条件四边形ABCD是菱形，可以使得四边形EFGH是矩形，理由如下，

如图，连接AC，BD，

E、F分别是AB，BC的中点

为的中位线

同理可得

四边形EFGH为平行四边形，

四边形ABCD是菱形，

四边形EFGH是矩形．

23．（1）解：∵正方形和正方形，

∴，，，

∴，

∴，

∴．

（2）如图，记，的交点为，记，的交点为，

∵，

∴，

∵，，

∴，

∴．

24．（1）证明：∵，，

∴，

∵四边形是平行四边形，

∴，

∴，

∵，

∴，

∴，

∴四边形是平行四边形，

∵，，

∴四边形是正方形；

（2）证明：∵，

∴，

∵，，

∴，

∴；

（3）证明：∵四边形是正方形，

∴，，

∴．