中考数学专题练——专题6 一次函数及其应用(试题精选，含答案)

这是一份中考数学专题练——专题6 一次函数及其应用(试题精选，含答案)，共42页。试卷主要包含了一次函数及其应用等内容，欢迎下载使用。


专题六 一次函数及其应用
一、单选题
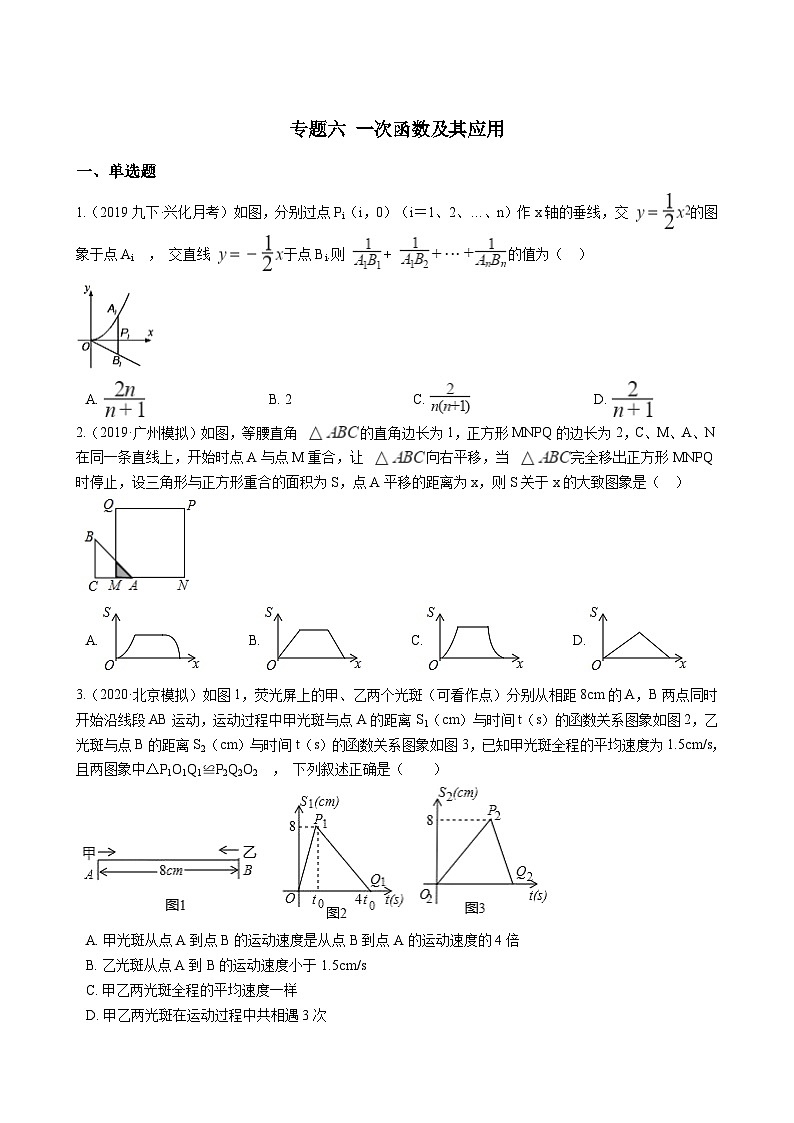
1.（2019九下·兴化月考）如图，分别过点Pi（i，0）（i＝1、2、…、n）作x轴的垂线，交 的图象于点Ai ， 交直线 于点Bi.则 + 的值为（   ）

A.                                   B. 2                                  C.                                   D. 
2.（2019·广州模拟）如图，等腰直角 的直角边长为1，正方形MNPQ的边长为2，C、M、A、N在同一条直线上，开始时点A与点M重合，让 向右平移，当 完全移出正方形MNPQ时停止，设三角形与正方形重合的面积为S，点A平移的距离为x，则S关于x的大致图象是（   ）

A.              B.              C.              D. 
3.（2020·北京模拟）如图1，荧光屏上的甲、乙两个光斑（可看作点）分别从相距8cm的A，B两点同时开始沿线段AB运动，运动过程中甲光斑与点A的距离S1（cm）与时间t（s）的函数关系图象如图2，乙光斑与点B的距离S2（cm）与时间t（s）的函数关系图象如图3，已知甲光斑全程的平均速度为1.5cm/s，且两图象中△P1O1Q1≌P2Q2O2 ， 下列叙述正确是（　　）

A. 甲光斑从点A到点B的运动速度是从点B到点A的运动速度的4倍
B. 乙光斑从点A到B的运动速度小于1.5cm/s
C. 甲乙两光斑全程的平均速度一样
D. 甲乙两光斑在运动过程中共相遇3次
4.（2020·台州）如图1，小球从左侧的斜坡滚下，到达底端后又沿着右侧斜坡向上滚，在这个过程中，小球的运动速度v（单位:m/s）与运动时间t （单位:s）的函数图象如图2，则该小球的运动路程y（单位:m）与运动时间t（单位:s）之间的函数图象大致是（    ）

A.               B.               C.               D. 
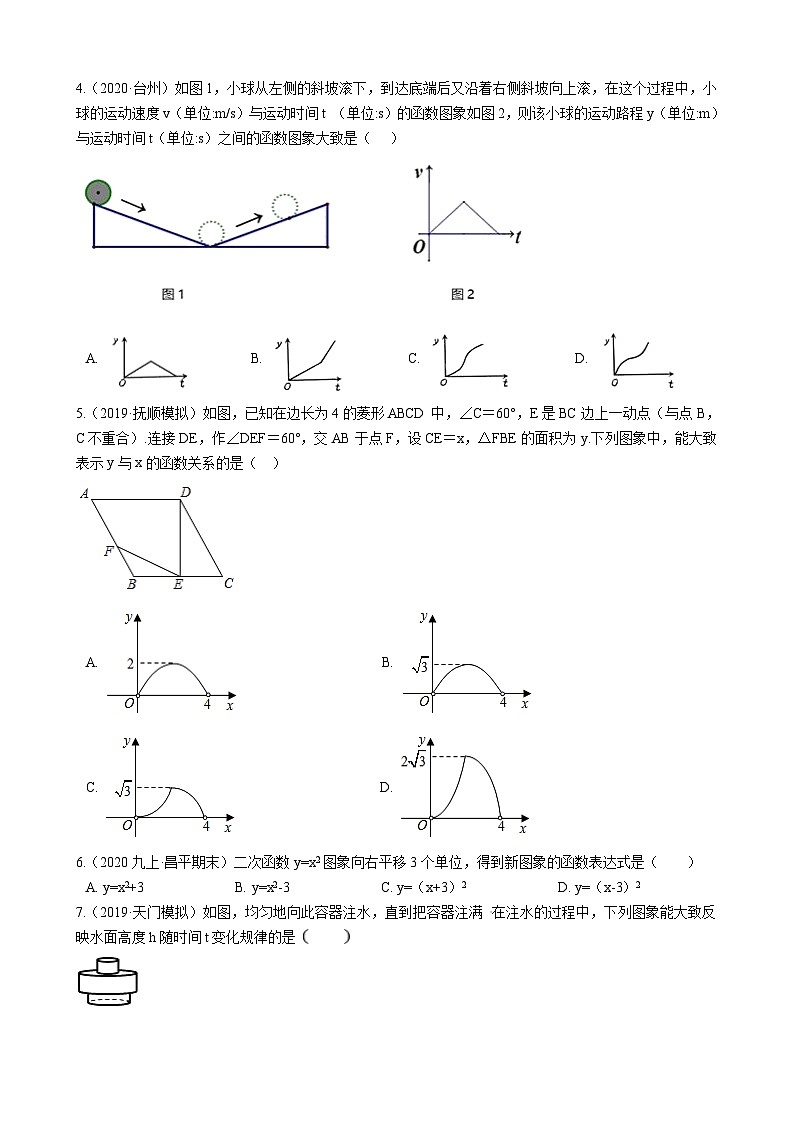
5.（2019·抚顺模拟）如图，已知在边长为4的菱形ABCD中，∠C＝60°，E是BC边上一动点（与点B，C不重合）.连接DE，作∠DEF＝60°，交AB于点F，设CE＝x，△FBE的面积为y.下列图象中，能大致表示y与x的函数关系的是（   ）

A.                                         B. 
C.                                         D. 
6.（2020九上·昌平期末）二次函数y=x2图象向右平移3个单位，得到新图象的函数表达式是（　　）
A. y=x2+3                          B. y=x2-3                          C. y=（x+3）2                          D. y=（x-3）2
7.（2019·天门模拟）如图，均匀地向此容器注水，直到把容器注满 在注水的过程中，下列图象能大致反映水面高度h随时间t变化规律的是 　　

A.                  B.                  C.                  D. 
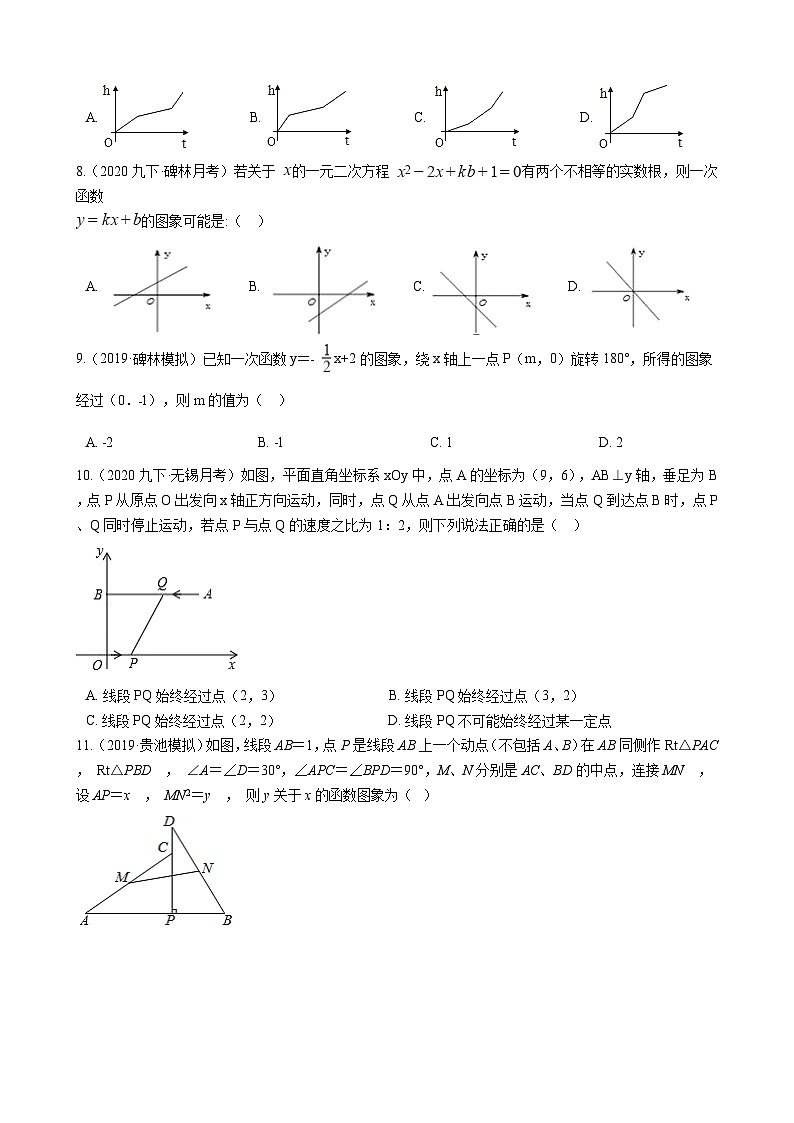
8.（2020九下·碑林月考）若关于 的一元二次方程 有两个不相等的实数根，则一次函数
的图象可能是:（   ）
A.         B.         C.         D. 
9.（2019·碑林模拟）已知一次函数y＝﹣ x+2的图象，绕x轴上一点P（m，0）旋转180°，所得的图象经过（0．﹣1），则m的值为（   ）
A. ﹣2                                         B. ﹣1                                         C. 1                                         D. 2
10.（2020九下·无锡月考）如图，平面直角坐标系xOy中，点A的坐标为（9，6），AB⊥y轴，垂足为B，点P从原点O出发向x轴正方向运动，同时，点Q从点A出发向点B运动，当点Q到达点B时，点P、Q同时停止运动，若点P与点Q的速度之比为1：2，则下列说法正确的是（   ）

A. 线段PQ始终经过点（2，3）                              B. 线段PQ始终经过点（3，2）
C. 线段PQ始终经过点（2，2）                              D. 线段PQ不可能始终经过某一定点
11.（2019·贵池模拟）如图，线段AB＝1，点P是线段AB上一个动点（不包括A、B）在AB同侧作Rt△PAC ， Rt△PBD ， ∠A＝∠D＝30°，∠APC＝∠BPD＝90°，M、N分别是AC、BD的中点，连接MN ， 设AP＝x ， MN2＝y ， 则y关于x的函数图象为（   ）

A.                                             B. 
C.                                            D. 
12.（2019·黄冈模拟）如图，在平面直角坐标系中，四边形 是菱形，点C的坐标为 ， ，垂直于 轴的直线 从y轴出发，沿x轴正方向以每秒1个单位长度的速度向右平移，设直线 与菱形 的两边分别交于点M，N(点M在点N的上方)，若 的面积为S，直线 的运动时间为 秒 ，则能大致反映S与 的函数关系的图象是(   )

A.                                            B. 
C.                                             D. 
13.（2020九上·德清期末）如图1，在菱形ABCD中，∠A＝120°，点E是BC边的中点，点P是对角线BD上一动点，设PD的长度为x，PE与PC的长度和为y，图2是y关于x的函数图象，其中H是图象上的最低点，则a+b的值为（   ）

A. 7                                  B.                                  C.                                  D. 
14.（2020·遵化模拟）如图，一次函数与x轴，y轴的交点分别是A（－4，0），B（0，2）.与反比例函数的图像交于点Q，反比例函数图像上有一点P满足：① PA⊥x轴；②PO＝ （O为坐标原点），则四边形PAQO的面积为（   ）

A. 7                                    B. 10                                    C. 4+2                                     D. 4-2
15.（2019·郑州模拟）如图，在平面直角坐标系中，将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1 ， 依此方式，绕点O连续旋转2018次得到正方形OA2018B2018C2018 ， 如果点A的坐标为（1，0），那么点B2018的坐标为（    ）

A. （1，1）                     B. （0， ）                     C. （ ）                     D. （﹣1，1）
16.（2019·唐县模拟）超市有A，B两种型号的瓶子，其容量和价格如表，小张买瓶子用来分装15升油（瓶子都装满，日无剩油）；当日促销活动：购买A型瓶3个或以上，一次性返还现金5元.设购买A型瓶x（个），所需总费用为y（元），则下列说法不一定成立的是（   ）
型号
A
B
单个瓶子容量（升）
2
3
单价（元）
5
6
A. 购买B型瓶的个数是（5 - x）为正整数时的值     B. 购买A型瓶最多为6个
C. y与x之间的函数关系式为y=x+30                            D. 小张买瓶了的最少费用是28元
17.（2020九上·南昌期末）如图，直线y＝ x＋ 与x轴、y轴分别相交于A、B两点，圆心P的坐标为（1，0），⊙P与y轴相切于点O．若将⊙P沿x轴向左移动，当⊙P与该直线相交时，满足横坐标为整数的点P的个数是（     ）

A. 3                                           B. 4                                           C. 5                                           D. 6
18.（2019·颍泉模拟）如图1，矩形ABCD中，AB＝4，AD＝2，E、F是边AB、DC的中点，连接EF、AF，动点P从A向F运动，AP＝x，y＝PE+PB．图2所示的是y关于x的函数图象，点（a，b）是函数图象的最低点，则a的值为（   ）

A.                                      B.                                      C.                                      D. 2
19.（2019九上·许昌期末）如图，已知△ABC的顶点坐标分别为A(0，2)，B(1，0)，C(2，1).若二次函数y=x2+bx+1的图像与阴影部分(含边界)一定有公共点，则实数b的取值范围是（   ）

A. b≤-2                                   B. b<-2                                   C. b≥-2                                   D. b>-2
20.（2019·润州模拟）如图，在平面直角坐标系中，对角线为1的正方形OABC，点A在x轴的正半轴上，如果以对角线OB为边作第二个正方形OBB1C1 ， 再以对角线OB1为边作第三个正方形OBlB2C2 ， 照此规律作下去，则点B2019的坐标为（   ）

A. （﹣21009 ， 21009）                                        B. （21008 ， ﹣21008）
C. （﹣21009 ，0）                                          D. （0，21008 ）
二、填空题
21.（2020九上·南昌期末）如图，平行于x轴的直线AC分别交抛物线y1=x2（x≥0）与y2= （x≥0）于B、C两点，过点C作y轴的平行线交y1于点D，直线DE∥AC，交y2于点E，则 =________．

22.（2019九下·临洮期中）如图，直线y=3x和y=kx+2相交于点P（a，3），则不等式3x≥kx+2的解集为________.

23.（2019·金昌模拟）如图，已知函数y＝ax+b和y＝kx的图象交于点P，则根据图象可得，关于 的二元一次方程组的解是________.

24.（2019·润州模拟）在直角坐标系中，点E（10，0），F（0，5），A（﹣1，0），D（0，2），四边形ABCD为菱形，且点B、C在第二象限，向右平移菱形ABCD，平移的距离为d，当点B在△EOF边及内部时，d的范围是________.

25.（2020·西安模拟）若一次函数y=ax+b的图象与一次函数y=mx+n的图象相交，且交点在x轴上，则a、b、m、n满足的关系式是________.

26.（2020·南通模拟）如图，等边 的边长为2，则点B的坐标为________.

27.（2019九下·十堰月考）已知直线 与 轴的交点在A（2,0），B（3,0）之间（包括A、B两点）则 的取值范围是________.
28.（2019·徽县模拟）如图，点A1的坐标为（2，0），过点A1作x轴的垂线交直线l：y= x于点B1 ， 以原点O为圆心，OB1的长为半径画弧交x轴正半轴于点A2；再过点A2作x轴的垂线交直线l于点B2 ， 以原点O为圆心，以OB2的长为半径画弧交x轴正半轴于点A3；….按此作法进行下去，则 的长是________.

29.（2020九下·宝应模拟）如图所示，一次函数 （ 、 为常数，且 ）的图象经过点 ，则不等式 的解集为________．

30.（2019·上海模拟）已知一次函数y = kx + b图像不经过第二象限，那么b的取值范围是________.
31.（2020九上·路桥期末）对于实数a和b，定义一种新的运算“*”， ，计算 =________.若 恰有三个不相等的实数根 ，记 ，则k的取值范围是 ________.
32.（2020九上·常州期末）如图，在平面直角坐标系中，以O为圆心，6为半径画圆弧，与两坐标轴分别交于点A、B，已知点C（5， 0）、D（0， 3），P为AB上一点，则2PD+CP的最小值为________.

33.（2019九上·克东期末）如图，在平面直角坐标系中，将 绕点 顺指针旋转到 的位置，点 、 分别落在点 、 处，点 在 轴上，再将 绕点 顺时针旋转到 的位置，点 在 轴上，将 绕点 顺时针旋转到 的位置，点 在 轴上，依次进行下午……，若点 ， ，则点 的横坐标为________．

34.（2020九上·建湖月考）关于x的一元二次方程ax2－3x－1＝0的两个不相等的实数根都在－1和0之间（不含－1和0），则a的取值范围是________.
35.（2019九上·克东期末）如图，若直线 与 轴、 轴分别交于点 、 ，并且 ， ，一个半径为 的 ，圆心 从点 开始沿 轴向下运动，当 与直线 相切时， 运动的距离是________．

三、解答题
36.（2019九上·松滋期末）x1、x2是方程2x2—3x—6=0的二根，求过A（x1+x2 ， 0）B（0，xl·x2）两点的直线解析式.
37.（2019九上·越城月考）如图，我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A、B、C、D分别是“果圆”与坐标轴的交点，抛物线的解析式为y=(x-1)2-4，AB为半圆的直径，求这个“果圆”被y轴截得的CD的长.

38.（2019九上·伍家岗期末）如图，直线y＝﹣ x+4与x轴、y轴分别交于A、B两点，把△AOB绕点A顺时针旋转90°后得到△AO′B′，求点B′的坐标.

39.（2019·合肥模拟）《算法统宗》中记载了一个“李白沾酒”的故事，诗云：“今携一壶酒，游春郊外走。逢朋加一倍入店饮半斗.相逢三处店，饮尽壶中酒.试问能算士，如何知原有.”（注：古代一斗是10升）译文：李白在郊外春游时，做出这样一条约定；遇见朋友，先到酒店里将壶里的酒增加一倍，再喝掉其中的5升酒，按照这样的约定，在第3个店里遇到朋友时，李白正好喝光了壶中的酒，请问各位，壶中原有多少升酒？
40.（2019·宁洱模拟）求出函数y＝ ﹣1与坐标轴围成的三角形的面积.
41.（2019九下·中山月考）已知矩形PMON的边OM、ON分别在x、y轴上，O为坐标原点，且点P的坐标为（﹣2，3）．将矩形PMON沿x轴正方向平移4个单位，得到矩形P1M1O1N1再将矩形P1M1O1N1绕着点O1旋转90°得到矩形P2M2O2N2 ． 在坐标系中画出矩形P2M2O2N2 ， 并求出直线P1P2的解析式．
42.“五一”节假期间，小亮一家到某度假村度假，小亮和他妈妈坐公交车先出发，他爸爸自驾车沿着相同的道路后出发，他爸爸到达度假村后，发现忘了东西在家里，于是立即返回家里取，取到东西后又马上驾车前往度假村，如图是他们家的距离 （ ）与小明离家的时间 的关系图，请根据图回答下列问题：

（1）小亮和妈妈坐公交车的速度为________；爸爸自驾的速度为________.
（2）小亮从家到度假村期间，他离家的距离 与离家的时间 的关系式为________；小亮从家到度假村的路途中，当他与他爸爸相遇时，离家的距离是________.
（3）整个运动过程中（双方全部到达会和时，视为运动结束）， 为多少时小亮和妈妈与爸爸相距 ？


43.（2020·西安模拟）某商城的智能手机销售异常火爆，若销售10部A型和20部B型手机的利润共4000元，每部B型手机的利润比每部A型手机多50元．
（1）求每部A型手机和B型手机的销售利润．
（2）商城计划一次购进两种型号的手机共100部，其中B型手机的进货量不超过A型手机的2倍，则商城购进A型、B型手机各多少部，才能使销售利润最大？最大利润是多少？
44.（2019·河南模拟）某商店购进了一种新款小电器，为了寻找合适的销售价格，进行了为期5周的试营销，试营销的情况如表所示：

第1周
第2周
第3周
第4周
第5周
售价/（元/台）
50
40
60
55
45
销售/台
360
420
300
330
390
已知该款小电器的进价每台30元，设该款小电器每台的售价为x元，每周的销量为y台.
（1）观察表中的数据，推断y与x满足什么函数关系，并求出这个函数关系式；
（2）若想每周的利润为9000元，则其售价应定为多少元？
（3）若每台小电器的售价不低于40元，但又不能高于进价的2倍，则如何定价才能更快地减少库存？此时每周最多可销售多少台？
45.如图，直线y＝x+3与x轴、y轴分别相交于A、C两点，过点B（6，0），E（0，﹣6）的直线上有一点P，满足∠PCA＝135°.

（1）求证：四边形ACPB是平行四边形；


（2）求直线BE的解析式及点P的坐标.


46.（2019·泸西模拟）A市和B市分别有某种库存机器12台和6台，现决定支援C村10台，D村8台，已知从A市调运一台机器到C村和D村的运费分别是400元和800元，从B市调运一台机器到C村和D村的运费分别是300元和500元.
（1）设B市运往C村机器x台，求总运费W关于x的函数关系式；
（2）若要求总运费不超过9000元，共有几种调运方案？
（3）求出总运费最低的调运方案，最低运费是多少元？
分析由已知条件填出下表：
 
 库存机器
支援C村
支援D村
B市
6台
x台
（6﹣x）台
A市
12台
（10﹣x）台
[8﹣（6﹣x）]台
47.（2019·朝阳模拟）李明驾车以100千米/小时的速度从甲地匀速开往乙地，行驶到服务区休息了一段时间后以另一速度继续匀速行驶，直至到达乙地．李明与乙地的距离y（千米）与时间x（小时）之间的函数关系图象如图所示．

（1）求a的值；
（2）求李明从服务区到乙地y与x之间的函数关系式；
（3）求x＝5时李明驾车行驶的路程．
48.（2019·香坊模拟）在平面直角坐标系中，直线ABy＝kx﹣1分别交x轴、y轴于点A、B，直线CDy＝x+2分别交x轴、y轴于点D、C，且直线AB、CD交于点E，E的横坐标为﹣6．

（1）如图①，求直线AB的解析式；
（2）如图②，点P为直线BA第一象限上一点，过P作y轴的平行线交直线CD于G，交x轴于F，在线段PG取点N，在线段AF上取点Q，使GN＝QF，在DG上取点M，连接MN、QN，若∠GMN＝∠QNF，求 的值；
（3）在(2)的条件下，点E关于x轴对称点为T，连接MP、TQ，若MP∥TQ，且GN：NP＝4：3，求点P的坐标．
49.（2019·武汉模拟）如图，在平面直角坐标系中有三点A（2，4）、B（3，5）、P（a，a），将线段AB绕点P顺时针旋转90°得到CD，其中A、B的对应点分别为C、D;

（1）当a＝2时，
①在图中画出线段CD，保留作图痕迹，并直接写出C、D两点的坐标；
②将线段CD向上平移m个单位，点C、D恰好同时落在反比例函数y＝ 的图象上，求m和k的值．
（2）若a＝4，将函数y＝ （x＞0）的图象绕点P顺时针旋转90°得到新图象，直线AB与新图象的交点为E、F，则EF的长为________．（直接写出结果）
50.（2018九上·成都期中）有这样一个问题：探究同一坐标系中系数互为倒数的正、反比例函数 与 的图象性质 小明根据学习函数的经验，对这两个函数当 时的图象性质进行了探究 设函数 与 图象的交点为A、
下面是小明的探究过程：
（1）如图所示，若已知A的坐标为 ，则B点的坐标为________．

（2）若A的坐标为 ，P点为第一象限内双曲线上不同于点B的任意一点．
①设直线PA交x轴于点M，直线PB交x轴于点 求证： ．
证明过程如下：设 ，直线PA的解析式为 ．
则
解得
所以，直线PA的解析式为________．
请把上面的解答过程补充完整，并完成剩余的证明．
②当P点坐标为 时，判断 的形状，并用k表示出 的面积．

答案解析部分
一、单选题
1. A
【解答】根据题意得：
,
,
.
故答案为：A.
【分析】根据Ai的纵坐标与Bi纵坐标的绝对值之和为AiBi的长，分别表示出所求式子的各项，拆项后抵消即可得到结果.
2. C
【解答】解：当0＜x＜a时， ，此时为抛物线，排除B，D选项；
当 时， 为常数；
故答案为：C．
【分析】根据三角形在移动过程中，重合面积和x之间的关系建立分段函数，利用分段函数确定函数的图象即可；
3. C
【解答】解：∵甲到B所用时间为t0s，从B回到A所用时间为4t0﹣t0＝3t0
∵路程不变
∴甲光斑从A到B的速度是从B到A运动速度的3倍
∴A不符合题意
由于，△O1P1Q1≌△O2P2Q2
∵甲光斑全程平均速度1.5cm/s
∴乙光斑全程平均速度也为1.5cm/s
∵乙由B到A时间为其由A到B时间三倍
∴乙由B到A速度低于平均速度，则乙由A到B速度大于平均速度
∴B不符合题意
由已知，两个光斑往返总时间，及总路程相等，则两个光斑全程的平均速度相同
∴C符合题意
根据题意，分别将甲、乙光斑与点A的距离与时间的函数图象画在下图中，两个函数图象交点即为两个光斑相遇位置
故可知，两个光斑相遇两次，故D不符合题意．

故答案为：C．
【分析】甲乙两个光斑的运动路程与时间的图象，因为起始点不同，因而不易判断，如果根据题意将两个点运动的基准点变为同一个点，再根据题意解决问题.
4. C
【解答】解：小球从左侧的斜坡滚下是匀变速运动，运动的路程y是t的二次函数，图象是先缓后陡，
在右侧上升时，情形与左侧相反，
故答案为：C．
【分析】小球从左侧的斜坡滚下是匀变速运动，运动的路程y是t的二次函数，图象是先缓后陡，由此即可判断．
5. B
【解答】如图，延长CB至H，使BH=BF，

∵四边形ABCD是菱形，
∴BC=CD=4，AB∥CD，
∴∠ABH=∠C=60°，
∴△BFH是等边三角形，
∴∠H=60°，BF=BH=FH，
∵∠DEB=∠EDC+∠C=∠DEF+∠FEB，且∠DEF=60°=∠C，
∴∠FEB=∠EDC，且∠H=∠C=60°，
∴△DEC∽△EFH，
∴ ，
∴ ，
∴HF=x，
∴S= ×(4﹣x)× x= (x﹣2 + ，
∴该函数图象开口向下，当x=2时，最大值为 ，
故答案为：B.
【分析】如图，延长CB至H，使 ，通过证明 ，可得 ，可得 ，由三角形面积公式可求函数解析式，即可求解.
6. D
【解答】解：二次函数y=x2的图象向右平移3个单位，
得到新图象的函数表达式是：y=（x-3）2 ，
故答案为：D．
【分析】根据函数图象的平移变换法则“左加右减，上加下减”结合平移前的函数解析式，可得答案．
7. A
【解答】解：最下面的容器较粗，第二个容器最粗，那么第二个阶段的函数图象水面高度h随时间t的增大而增长缓慢，用时较长，最上面容器最小，那么用时最短，
故答案为：A.
【分析】由于三个容器的高度相同，粗细不同，那么水面高度h随时间t变化而分三个阶段.
8. B
【解答】解：由方程 有两个不相等的实数根,
可得 ，
解得 ，即 异号，
当 时，一次函数 的图象过一三四象限，
当 时，一次函数 的图象过一二四象限，
故答案为：B.
【分析】由方程 有两个不相等的实数根可知该方程根的判别式的值应该大于0，从而列出不等式，求解即可判断出k,b异号，然后分当 时与当 时两种情况根据一次函数的系数与图象的关系即可一一判断得出答案.
9. C
【解答】∵一次函数y＝﹣ x+2的图象，绕x轴上一点P（m，0）旋转180°，所得的图象经过（0．﹣1），
∴设旋转后的函数解析式为y＝﹣ x﹣1，
在一次函数y＝﹣ x+2中，令y＝0，则有﹣ x+2＝0，解得：x＝4，
即一次函数y＝﹣ x+2与x轴交点为（4，0）．
一次函数y＝﹣ x﹣1中，令y＝0，则有﹣ x﹣1＝0，解得：x＝﹣2，
即一次函数y＝﹣ x﹣1与x轴交点为（﹣2，0）．
∴m＝ ＝1，
故答案为：C．
【分析】根据题意得出旋转后的函数解析式为y=- x-1，然后根据解析式求得与x轴的交点坐标，结合点的坐标即可得出结论．
10. B
【解答】解：当OP=t时，点P的坐标为（t，0），点Q的坐标为（9﹣2t，6）.
设直线PQ的解析式为y=kx+b（k≠0），
将P（t，0）、Q（9﹣2t，6）代入y=kx+b，得，
，解得： ，
∴直线PQ的解析式为y= x+ .
∵x=3时，y=2，
∴直线PQ始终经过（3，2），
故答案为：B.
【分析】当OP=t时，点P的坐标为（t，0），点Q的坐标为（9﹣2t，6）.设直线PQ的解析式为y=kx+b（k≠0），利用待定系数法求出PQ的解析式即可判断；
11. B
【解答】解：连接PM、PN，则PM、PN分别为Rt△PAC，Rt△PBD的中线，

∵∠A＝∠D＝30°，则∠MAP＝∠A＝30°，
则PM＝ ＝ ，
同理PN＝ ＝1﹣x，
y＝MN2＝（PM）2+（PN）2＝ x2﹣2x+1，
函数的对称轴x＝﹣ = ，
故答案为：B．
【分析】连接PM、PN，则PM、PN分别为Rt△PAC，Rt△PBD的中线，则∠A＝∠D＝30°，则∠MAP＝∠A＝30°，则PM＝ ＝ ，PN＝ ＝1﹣x，即可求解．
12. A
【解答】过A作AD⊥x轴于D，
 
∵OA=OC=4，∠AOC=60°，
∴OD=2，
由勾股定理得： ，
①当 时， ， ， ；
② 时， ， ，
故答案为：A.
【分析】过A作AD⊥x轴于D，根据勾股定理和含30度角的直角三角形的性质求出AD，分两种情况①当 时，② 时，分别利用三角形的面积公式即可求出答案.
13. C
【解答】解：∵在菱形ABCD中，∠A＝120°，点E是BC边的中点，
∴易证AE⊥BC，
∵A、C关于BD对称，
∴PA＝PC，
∴PC+PE＝PA+PE，
∴当A、P、E共线时，PE+PC的值最小，即AE的长.
观察图象可知，当点P与B重合时，PE+PC＝6，
∴BE＝CE＝2，AB＝BC＝4，
∴在Rt△AEB中，BE＝ ，
∴PC+PE的最小值为 ，
∴点H的纵坐标a＝ ，
∵BC∥AD，
∴ ＝2，
∵BD＝ ，
∴PD＝ ，
∴点H的横坐标b＝ ，
∴a+b＝ ；
故答案为：C.
【分析】由A、C关于BD对称，推出PA＝PC，推出PC+PE＝PA+PE，推出当A、P、E共线时，PE+PC的值最小，观察图象可知，当点P与B重合时，PE+PC＝6，推出BE＝CE＝2，AB＝BC＝4，分别求出PE+PC的最小值，PD的长即可解决问题.
14. C
【解答】解：设一次函数解析式为y=kx+b，将点A以及点B坐标代入可知，b=2，k=
∴一次函数解析式为y=x+2；
设P点的坐标为（-4，m）
∴（-4）2+m2=17
∴m=±1
∴m=-1
∴点P为（-4，-1）
设反比例函数解析式为y=， 代入（-4，-1），解得n=4
∴反比例函数解析式为y=
将一次函数和反比例函数解析式联立，， 解得
∴Q点的坐标为（2-2，+1）
∴S四边形PAOQ=S△APO+S△AOQ
故答案为：C.

【分析】根据点A和点B的坐标，计算得到AB的解析式，继而由PO的长度，求出点P的坐标，随机得到反比例函数的解析式，根据题意，将两个函数解析式联立，得到交点Q的坐标，将四边形的面积转化为两个三角形的面积即可。
15. D
【解答】解：∵四边形OABC是正方形，且OA=1，
∴B（1，1），
连接OB，

由勾股定理得：OB= ，
由旋转得：OB=OB1=OB2=OB3=…= ，
∵将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1 ，
相当于将线段OB绕点O逆时针旋转45°，依次得到∠AOB=∠BOB1=∠B1OB2=…=45°，
∴B1（0， ），B2（-1，1），B3（- ，0），…，
发现是8次一循环，所以2018÷8=252…余2，
∴点B2018的坐标为（-1，1）
故答案为：D．
【分析】根据图形可知：点B在以O为圆心，以OB为半径的圆上运动，由旋转可知：将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1 ， 相当于将线段OB绕点O逆时针旋转45°，可得对应点B的坐标，根据规律发现是8次一循环，可得结论．
16. C
【解答】解：设购买A型瓶x个，
∵买瓶子用来分装15升油，瓶子都装满，且无剩油，
∴购买B型瓶的个数是15−2x3=5−23x，
∵瓶子的个数为自然数，
∴x=0时,5−23x=5;x=3时,5−23x=3;x=6时,5−23x=1；
∴购买B型瓶的个数是(5−23x)为正整数时的值，故A成立；
由上可知，购买A型瓶的个数为0个或3个或6个，所以购买A型瓶的个数最多为6，故B成立；
设购买A型瓶x(个),所需总费用为y(元),则购买B型瓶的个数是(5−23x)个，
①当0⩽x<3时,y=5x+6×(5−23x)=x+30，
∵k=1>0，
∴y随x的增大而增大，
∴当x=0时，y有最小值，最小值为30元；
②当x⩾3时,y=5x+6×(5−23x)−5=25+x，
∵k=1>0，
∴y随x的增大而增大，
∴当x=3时，y有最小值，最小值为28元；
综合①②可得，购买盒子所需要最少费用为28元。
故C不成立，D成立。
故答案为：C.

【分析】根据A，B两种型号的瓶子的容量以及买瓶子用来分装15升油（瓶子都装满，且无剩油），可得购买B型瓶的个数是， 再根据实际意义即可判断A；
根据购买B型瓶的个数是（5-）为正整数时的值即可判断B；
分两种情况讨论：①当0≤x<3时；②当x≥3时，分别求出y与x之间的函数关系式，即可判断C；
根据C中求出的解析式，利用一次函数的性质即可判断D．
17. A
【解答】解：根据直线与坐标轴的交点，得出A，B的坐标，再利用三角形相似得出圆与直线相切时的坐标，进而得出相交时的坐标．

∵直线y＝ x＋ 与x轴、y轴分别相交于A、B两点，圆心P的坐标为（1，0），
∴A点的坐标为0＝ x＋
x=-3，A（-3，0），
B点的坐标为：（0， ），
∴AB=2
将圆P沿x轴向左移动，当圆P与该直线相切于C1时，P1C1=1，
根据△AP1C1∽△ABO，

∴AP1=2，
∴P1的坐标为：（-1，0），
将圆P沿x轴向左移动，当圆P与该直线相切于C2时，P2C2=1，
根据△AP2C2∽△ABO，

∴AP2=2，
P2的坐标为：（-5，0），
从-1到-5，整数点有-2，-3，-4，故横坐标为整数的点P的个数是3个．
故答案为：A．
【分析】先求出函数与x轴、y轴的交点坐标，进一步求出函数与x轴的夹角，计算出 ⊙P 与AB相切时点P的坐标，判断出P的横坐标的取值范围.
18. B
【解答】解：∵矩形ABCD，E、F是边AB、DC的中点，AB＝4，AD＝2
∴易证四边形ADFE是正方形
∴点E关于EF的对称点是点D
∴PE＝PD
∴y＝PE+PB＝PD+PB
∴当点D、P、B三点共线时，y取得最小值b
连接BD交于点P1 ， 此时AP1＝a，BD＝b，如图：

∵AB∥CD
∴
∴AP1＝ AF＝ × ＝
即a＝ ．
故答案为：B．
【分析】由已知易得四边形ADFE是正方形，进而利用轴对称的性质得当点D、P、B三点共线时，y取得最小值b，此时AP1＝a，BD＝b，最后利用相似三角形的判定与性质以及勾股定理计算出a的值．
19. C
【解答】当二次函数y=x2+bx+1的图象经过点B（1，0）时，1+b+1=0.解得b=-2，故排除B、D；
因为y=x2+bx+1与y轴交于点（0，1），所以（0，1）与点C关于直线x=1对称，当对称轴x≤1时，二次函数y=x2+bx+1与阴影部分一定有交点，所以- ≤1，解得b≥-2，故答案为：C.
【分析】根据y=x2+bx+1与y轴交于点（0，1），且与点C关于x=1对称，则对称轴x≤1时，二次函数y=x2+bx+1与阴影部分一定有交点，据此可求出b的取值范围.
20. C
【解答】∵正方形OABC对角线OB＝1，正方形OBB1C1是正方形OABC的对角线OB为边，
∴OB1＝ ，
∴B1点坐标为（0， ），
同理可知OB2＝2，B2点坐标为（﹣ ， ），
同理可知OB3＝2 ，B3点坐标为（﹣2 ，0），
B4点坐标为（﹣2 ，﹣2 ），B5点坐标为（0，﹣4 ），
B6（4 ，﹣4 ），B7（8 ，0），
B8（8 ，8 ），B9（0，16 ），
由规律可以发现，每经过8次作图后，点的坐标符号与第一次坐标符号相同，每次正方形的边长变为原来的 倍，
∵2019÷8＝252…3，
∴B2019的纵横坐标符号与点B3的相同，横坐标为负值，纵坐标是0，
∴B2019的坐标为（﹣21009 ，0）.
故答案为：C.
【分析】首先求出B1、B2、B3、B4、B5、B6、B7、B8、B9的坐标，找出这些坐标的之间的规律，然后根据规律计算出点B2019的坐标.
二、填空题
21. 3﹣
【解答】设点B的横坐标为 ，则
∵平行于x轴的直线AC
∴
又∵CD平行于y轴
∴
又∵DE∥AC
∴
∴
∴ =3﹣
【分析】首先设点B的横坐标，由点B在抛物线y1=x2（x≥0）上，得出点B的坐标，再由平行，得出A和C的坐标，然后由CD平行于y轴，得出D的坐标，再由DE∥AC，得出E的坐标，即可得出DE和AB，进而得解.
22. x≥1
【解答】∵直线y=3x和直线y=kx+2的图象相交于点P（a，3），
∴3=3a，解得a=1，
∴P（1，3），
由函数图象可知，当x≥1时，直线y=3x的图象在直线y=kx+2的图象的上方，
即当x≥1时，3x≥kx+2，
故答案为x≥1.
【分析】先把点P（a，3）代入直线y=3x求出a的值，故可得出P点坐标，再根据函数图象进行解答即可.
23. x=1,y=1
【解答】解：函数y=ax+b和y=kx的图象交于点P（1，1）
即x=1，y=1同时满足两个一次函数的解析式.
所以，方程组 的解是 ,
故答案为x=1,y=1.
【分析】由图可知：两个一次函数的交点坐标为（1，1）；那么交点坐标同时满足两个函数的解析式，而所求的方程组正好是由两个函数的解析式所构成，因此两函数的交点坐标即为方程组的解.
24. 1＜d＜11+
【解答】∵四边形ABCD是菱形，A（﹣1，0），D（0，2），
∴AD＝ ＝AB
若点B在x轴负半轴上，点B坐标为（﹣1﹣ ，0）
当点C在y轴正半轴上，点B坐标为（﹣1， ）
∵向右平移菱形ABCD，平移的距离为d，当点B在△EOF边及内部时，
∴1＜d＜11+
故答案为：1＜d＜11+
【分析】由菱形的性质和勾股定理可求AD=AB= ，由特殊点位置的平移求出d的范围.
25. an=bm
【解答】解：∵若一次函数y=ax+b的图象与一次函数y=mx+n的图象相交，且交点在x轴上，
∴把y=0代入y=ax+b，得：
0=ax+b，
解得，
∴交点坐标为（， 0）.
把（， 0）代入y=mx+n，得：
0=m·()+n，
整理得：an=mb.
∴a、b、m、n满足的关系式an=bm.
故答案为：an=bm.
【分析】根据交点在x轴上，把y=0代入y=ax+b，求出交点坐标为（， 0）.再把此交点坐标代入第二个函数解析式y=mx+n，整理出a、b、m、n之间的关系式.
26. .
【解答】解：如图，过B作BD⊥OA于D，则∠BDO=90°，

∵△OAB是等边三角形，

在Rt△BDO中，由勾股定理得： .
∴点B的坐标为： .
故答案为： .
【分析】过B作BD⊥OA于D，则∠BDO=90°，根据等边三角形性质求出OD，根据勾股定理求出BD，即可得出答案．
27.
【解答】解：由题意得 即
而 的取值范围为： 即 从而解出 .
故答案为：.
【分析】根据直线与x轴交点的纵坐标为0，将y=0代入 算出对应的自变量的值，然后根据该直线与x轴的交点在 A（2,0），B（3,0）之间（包括A、B两点） 即可列出关于a的不等式组，求解即可.
28.
【解答】直线y= x，点A1坐标为（2，0），过点A1作x轴的垂线交直线于点B1可知B1点的坐标为（2，2 ），
以原O为圆心，OB1长为半径画弧x轴于点A2 ， OA2=OB1 ，
OA2= =4，点A2的坐标为（4，0），
这种方法可求得B2的坐标为（4，4 ），故点A3的坐标为（8，0），B3（8，8 ）
以此类推便可求出点A2019的坐标为（22019 ， 0），
则 的长是 ，
故答案为： .
【分析】先根据一次函数方程式求出B1点的坐标，再根据B1点的坐标求出A2点的坐标，得出B2的坐标，以此类推总结规律便可求出点A2019的坐标，再根据弧长公式计算即可求解，.
29. ．
【解答】函数 的图象如图所示，图象经过点 ，且函数值 随 的增大而增大，
故不等式 的解集是 ．
故答案为： ．
【分析】由于一次函数y=ax+b（a、b为常数，且a＞0）的图象经过点A（4，1），再根据图象得出函数的增减性，即可求出不等式ax+b＜1的解集．
30. b≤0
【解答】不经过第二象限，可以只经过一，三象限或经过一，三，四象限
故b≤0
故填：b≤0.
【分析】根据一次函数的性质即可求解.
31. ；
【解答】当 时，即 时，

当 时，即 时，

；
设y= ，则y=
其函数图象如图所示，抛物线顶点 ，

根据图象可得：
当 时， 恰有三个不相等的实数根，
其中设 ，为 与 的交点， 为 与 的交点，
，
，
时， ，

故答案为： ；
【分析】分当 时，当 时两种情况，分别代入新定义的运算算式即可求解；设y= ，绘制其函数图象，根据图象确定m的取值范围，再求k的取值范围.
32. 13
【解答】在y轴上找一点E，使AE=OA=6，

∵D（0， 3），
∴OD=3，
∵∠DOP=∠POE， ，
∴∆DOP~∆POE，
∴ ，即：PE=2PD，
∴2PD+CP=PE+CP，
当点C，P，E三点共线时，2PD+CP=PE+CP的值最小，
∴2PD+CP的最小值= .
故答案是：13.
【分析】在y轴上找一点E，使AE=OA=6，易证∆DOP~∆POE，从而可得PE=2PD，进而根据两点之间线段最短，即可求解.
33.
【解答】因为 ， ，所以0A= ，OB=4，所以AB= = ,所以 （10,4）， （20,4）， （30,4）， （10090,4）， 的横坐标为10090+ + =10096.
【分析】由图形规律可知 在X轴上，根据观察 的规律即可解题.
34. −
【解答】解：∵关于x的一元二次方程ax2−3x−1=0的两个不相等的实数根
∴△=(−3)2−4×a×(−1)>0，
解得：a>−
设y=ax2−3x−1，如图，

∵实数根都在−1和0之间，
∴−1<−−a<0，
∴a<−，
且有当x=-1时，y<0, 当x=0时，y<0，
即a×(−1)2−3×(−1)−1<0, a×02−3×0−1=−1<0，
解得：a<−2，
∴− 故答案为：− 【分析】首先根据根的情况利用根的判别式解得a的取值范围，然后根据根两个不相等的实数根都在-1和0之间（不包括-1和0），结合函数图象根据对称轴和当x=1和x=0时确定其函数值的取值范围求解即得a的取值范围．
35. 3或7
【解答】设第一次相切的切点为 E ， 第二次相切的切点为 F ， 连接EC′，FC″，
在 Rt△BEC′中，∠ABC＝30°，EC′＝1，
∴BC′＝2EC′＝2，
∵BC＝5，
∴CC′＝3，
同法可得 CC″＝7，
故答案为 3 或 7．

【分析】分圆运动到第一次与AB相切，继续运算到第二次与AB相切两种情况，画出图形进行求解即可得.
三、解答题
36. 解：根据根与系数的关系
通过解方程可知
设两点的直线解析式y=kx+b，
 
解得k=2，b=−3，
∴过AB的直线是y=2x−3.
故两点的直线解析式y=2x−3.
【分析】首先设两点的直线解析式y=kx+b，利用根与系数的关系确定两点的坐标，代入可确定直线的解析式.
37. 解：连结CM，

当y=0时，（x-1）2-4=0,
解得x1=-1,x2=3.
∴A(-1,0),B(3,0)
∴AB=4，
又∵M为AB的中点，∴M（1,0）
∴OM=1,CM=2,∴CO= .
当x=0时y=-3,∴OD=3
∴CD=3+
【分析】先求得抛物线y=(x-1)2-4与x轴的交点A、B的坐标及与y轴交点D的坐标，即可求得OM、MC的长，由勾股定理求出OC的长，由CD=OC+OD即求求得CD的长.
38. 解：令x=0得y=3，则OA=3，令y=0得，x=4，则OB=4，
由旋转的性质可知：O′A=3，O′B′=4.
则点B′（7，3）.
故答案为：（7，13）.
【分析】根据直线与x轴相交，y=0，可得关于x的方程，解方程可求得点A的坐标，再根据旋转的性质即可求解.
39. 解：假设壶中原来有x升酒。
2[2（2x-5）-5]-5=0
4x-15=
4x=
x=
x=4.375
【分析】可以设壶中原来有x升酒，根据题意列出方程，解方程得到答案即可。
40. 解：∵y＝ ﹣1＝ ﹣1＝x﹣1；
∴y＝x﹣1，
∵函数y＝x﹣1与x，y轴的交点坐标分别为（1，0），（0，﹣1），
∴S＝ .
答：函数与坐标轴围成的三角形面积 .
【分析】化简函数y＝x﹣1，分别求出与x，y轴的交点坐标分别为（1，0），（0，﹣1），即可求三角形面积；
41. 解：如图所示：

当将矩形P1M1O1N1绕着点O1顺时针旋转90°得到矩形P2M2O2N2 ．
∵点P的坐标为（﹣2，3）．将矩形PMON沿x轴正方向平移4个单位，得到矩形P1M1O1N1 ，
∴P1的坐标为（2，3），
∵将矩形P1M1O1N1绕着点O1顺时针旋转90°得到矩形P2M2O2N2 ．
∴P2的坐标为（7，2），
设P1P2的解析式为：y＝kx+b，把P1（2，3），P2（7，2）代入得，2k+b＝3①，7k+b＝2②，
解由①②组成的方程组得，k＝﹣ ，b＝ ．
所以直线P1P2的解析式为y＝﹣ x + ；
当将矩形P1M1O1N1绕着点O1逆时针旋转90°得到矩形P2M2O2N2 ． 如图，

∴P2的坐标为（1，﹣2），
设P1P2的解析式为：y＝kx+b，把P1（2，3），P2（1，﹣2）代入得，2k+b＝3①，k+b＝﹣2②，
解由①②组成的方程组得，k＝5，b＝﹣7．
所以直线P1P2的解析式为y＝5x﹣7；
故答案为矩形P2M2O2N2见解析；当将矩形P1M1O1N1绕着点O1顺时针旋转90°得到矩形P2M2O2N2 ， 直线P1P2的解析式为：y＝﹣ x + ；当将矩形P1M1O1N1绕着点O1逆时针旋转90°得到矩形P2M2O2N2 ， 直线P1P2的解析式为：y＝5x﹣7.
【分析】由点P的坐标为（﹣2，3）．将矩形PMON沿x轴正方向平移4个单位，得到矩形P1M1O1N1 ， 得到P1的坐标为（2，3）．将矩形P1M1O1N1绕着点O1顺时针旋转90°得到矩形P2M2O2N2 ， 得P2的坐标为（7，2）；当将矩形P1M1O1N1绕着点O1逆时针旋转90°得到矩形P2M2O2N2 ， 得P2的坐标为（1，﹣2），然后利用待定系数法分别求出它们的直线解析式．
四、综合题
42. （1）20；60



（2）s=20t；30或45



（3）解：当 时，令 ，则 ，得 ，


当 时，令 ，解得， 或 ，
当 时， ，解得， 或
当 时，设小亮爸爸离家的距离 与离家的时间 的关系式为： ， ，解得 ，
当 时，小亮爸爸离家的距离 与离家的时间 的关系式为： ，
令 ，得 ，
由上可得， 为 、 、 、 、 、 时小亮和妈妈与爸爸相距 .


【解答】解：（1）由图可得，
 
小亮和妈妈坐公交车的速度为：60÷3=20（km/h），
爸爸自驾的速度为：60÷（2-1）=60（km/h），
故答案为：20，60；
（ 2 ）小亮和妈妈坐公交车的速度为20km/h，
小亮从家到度假村期间，他离家的距离 与离家的时间 的关系式为： ；
当 时，设小亮爸爸离家的距离 与离家的时间 的关系式为： ，
，解得 ，
即当 时，小亮爸爸离家的距离 与离家的时间 的关系式为： ；
当 时，设小亮爸爸离家的距离 与离家的时间 的关系式为：
， ，解得 ，
即当 时，小亮爸爸离家的距离 与离家的时间 的关系式为： .
令 ，得 ，此时， ，
令 ，得 ，此时 .
故答案为：s=20t；30或45.
【分析】（1）根据函数图象可以分别求得小亮和妈妈坐公交车的速度和爸爸自驾的速度；（2）根据题意利用待定系数法分段可以求得相应的函数解析式；小亮与爸爸相遇在图中即表示两个函数图象的交点，求出交点坐标，即可得出结果；（3）根据函数图象和各段对应的函数解析式，再根据小亮和妈妈与爸爸相距10km列方程求解.
 
43. （1）解：设每部A型手机和B型手机的销售利润分别为a元、b元，
，
解得， ，
答：每部A型手机和B型手机的销售利润分别为100元、150元；

（2）解：设购进A型手机x部，利润为w元，
w＝100x+150（100﹣x）＝﹣50x+15000，
∵100﹣x≤2x，
解得，x≥ ，
∵x为整数，
∴x＝34时，w取得最大值，此时w＝﹣50×34+15000＝13300，100﹣x＝66，
答：商城购进A型、B型手机分别为34部、66部时，才能使销售利润最大，最大利润是13300元．
【分析】（1）根据题意可以列出相应的二元一次方程组，从而可以求得每部A型手机和B型手机的销售利润；（2）根据题意可以写出利润和购买A型手机数量的函数关系式，然后利用一次函数的性质即可解答本题．
44. （1）解：y与x满足一次函数关系，
设y与x的函数关系式为y＝kx+b，
，得 ，
即这个函数关系式是y＝﹣6x+660

（2）解：（x﹣30）（﹣6x+660）＝9000，
解得，x1＝60，x2＝80，
答：若想每周的利润为9000元，则其售价应定为每台60元或每台80元

（3）解：由题意可得，
40≤x≤30×2，
即40≤x≤60，
∵y＝﹣6x+660，
∴当x＝40时，y取得最大值，此时y＝420，
答：定价为40元/台时，才能更快地减少库存，此时每周最多可销售420台
【分析】（1）根据题意和表格中的数据可以判断出y与x的函数关系式，并求出这个函数关系式；（2）根据题意可以得到每周的利润为9000元，则其售价应定为多少元；（3）根据题意和（1）中的函数关系式，利用一次函数的性质可以解答本题.
45. （1）证明：∵直线y＝x+3与x轴、y轴分别相交于A、C两点，


∴点A的坐标为（﹣3，0），点C的坐标为（0，3），
∴OA＝OC.
∵∠AOC＝90°，
∴∠CAO＝45°.
∵∠PCA＝135°，
∴∠CAO+∠PCA＝180°，
∴AB∥CP.
∵点B的坐标为（6，0），点E的坐标为（0，﹣6），
∴OB＝OE.
∵∠BOE＝90°，
∴∠OBE＝45°，
∴∠CAO＝∠ABE＝45°，
∴AC∥BP，
∴四边形ACPB为平行四边形.

（2）解：设直线BE的解析式为y＝kx+b（k≠0），


将B（6，0）、E（0，﹣6）代入y＝kx+b，得：
，解得：
∴直线BE的解析式为y＝x﹣6.
∵AB∥CP，
∴点P的纵坐标是3，
∴点P的坐标为（9，3）.


【分析】（1）利用一次函数图象上点的坐标特征可求出点A、C的坐标，进而可得出∠CAO=45°，结合∠PCA=135°可得出∠CAO+∠PCA=180°，利用“同旁内角互补，两直线平行”可得出AB∥CP，同理可求出∠ABE=45°=∠CAO，利用“内错角相等，两直线平行”可得出AC∥BP，再利用平行四边形的判定定理可证出四边形ACPB为平行四边形；（2）由点B、E的坐标，利用待定系数法可求出直线BE的解析式，由AB∥CP可得出点P的纵坐标，再利用一次函数图象上点的坐标特征即可求出点P的坐标.
 
 
46. （1）解：根据题意得：
W=300x+500（6﹣x）+400（10﹣x）+800[12﹣（10﹣x）]=200x+8600.

（2）解：因运费不超过9000元
∴W=200x+8600≤9000，
解得x≤2.
∵0≤x≤6，
∴0≤x≤2.
则x=0，1，2，所以有三种调运方案

（3）解：∵0≤x≤2，且W=200x+8600，
∴W随x的增大而增大
∴当x=0时，W的值最小，最小值为8600元，
此时的调运方案是：B市运至C村0台，运至D村6台，A市运往C市10台，运往D村2台，最低总运费为8600元.
【分析】（1）给出B市运往C村机器x台，再结合给出的分析表，根据等量关系总运费=A运往C的钱+A运往D的钱+B运往C的钱+B运往D的钱，可得函数式；（2）列一个符合要求的不等式；（3）根据函数式的性质以及自变量的取值范围求解.
47. （1）解：a＝500﹣100×3＝200，
即a的值是200；

（2）解：设y与x之间的函数关系式为y＝kx+b，
，得 ，
即y与x之间的函数关系式为y＝﹣80x+520（4≤x≤6.5）

（3）解：当x＝5时，
y＝﹣80×5+520＝120，
500﹣120＝380（千米），
答：x＝5时，李明驾车行驶的路程为380千米．
【分析】（1）根据题意和函数图象中的数据可以求得a的值；（2）根据（1）中的结果和函数图象中的数据可以求得y与x的函数关系式；（3）将x＝5代入（2）中的函数解析式，可以求得y的值，从而可以求得x＝5时，李明驾车行驶的路程．
48. （1）解：将x＝﹣6代入y＝x+2中得y＝﹣4
∴E(﹣6，﹣4)，
将E(﹣6，﹣4)代入y＝kx﹣1中，
得﹣4＝﹣6k﹣1，解得k＝ ，
∴直线AB的解析式为y＝ x﹣1

（2）解：如图②，延长GF至H，使FH＝FQ，连接QH，

∵∠QFH＝90°，GN＝QF
∴QH＝ FQ＝ GN，∠NHQ＝45°
在y＝x+2中令x＝0，得y＝2，令y＝0，得x＝﹣2，
∴C(0，2)，D(﹣2，0)，
∴OC＝OD＝2
∵∠COD＝90°
∴∠OCD＝∠ODC＝45°
∵FG∥OC
∴∠DGF＝∠DCO＝45°，∠DFG＝∠COD＝90°
∴DG＝ FG，∠MGN＝∠NHQ＝45°
∵∠GMN＝∠QNF
∴△GMN∽△HNQ
∴
∴NH＝ MG
∵GN＝FQ＝FH
∴FN+GN＝FN+FH，即FG＝NH
∴DG＝ FG＝ NH＝ × MG＝2MG
∴DG＝DM+MG＝2MG
∴DM＝MG＝ DG
∴ = =

（3）解：如图③，点T与E关于x轴对称，

∴T(﹣6，4)
∵点P在直线BA第一象限上
∴设点P坐标为(p， p﹣1)(p＞2)
∵FG∥y轴
∴F(p，0)，G(p，p+2)，
∴PF＝ p﹣1，GF＝p+2
∴GP＝GF﹣PF＝ p+3
∵GN：NP＝4：3
∴FQ＝GN＝ GP＝
∴xQ＝p﹣ ，即Q( ，0)
设直线TQ解析式为：y＝ax+b
∴    解得：a＝
∵ = ，即点M为DG中点
∴M( ， )
设直线MP解析式为：y＝cx+d
∴    解得：c＝
∵MP∥TQ
∴a＝c，即
解得：p＝8
∴点P坐标为(8，3)
【分析】(1)把点E横坐标代入直线CD求得点E的坐标，再代入直线y＝kx﹣1中，即求得直线AB的解析式．(2)先求出点C、D坐标得到等腰Rt△OCD，由GF∥y轴得△DGF也是等腰直角三角形，易得DG＝ FG．故延长延长GF至H，使FH＝FQ构造等腰直角三角形．证明△GMN∽△HNQ，由对应线段成比例得NH＝ MG．再通过转化证明FG＝NH，代入计算得到DG＝2MG，即M为DG中点，进而求得 = ．(3)设点P横坐标为p，则能用p表示G、F、M的坐标，进而用p表示GP的长．由GN：NP＝4：3，求得用p表示GN的式子，又因为GN＝QF，即能用p表示Q的坐标．易求点T坐标，故能用待定系数法求直线TQ解析式中一次项系数a的式子(含p)．同理可求直线MP解析式中一次项系数c的式子(含p)，由MP∥TQ可得a＝c，即列得关于p的方程，求出p即得点P坐标．
49. （1）解：①根据题意作出图象如下：

C（4，2），D（5，1），
②C点向上平移m个单位后点坐标为（4，2+m），
D点向上平移m个单位后点坐标为（5，1+m），
∵点C、D恰好同时落在反比例函数y＝ 的图象上，
∴4（2+m）＝5（1+m），
解得m＝3，
∴平移后C点坐标为（4，5），代入y＝ ，
得到k＝20；

（2）
【解答】解：（2）设直线AB的解析式是y＝kx+b，将点A（2，4）、B（3，5）代入，
，
解得 ，
∴直线AB解析式为y＝x+2，
∴直线AB与新图象的交点在过A点与AB垂直的直线上，
∴该直线解析式为y＝﹣x+6，
反比例函数与y＝﹣x+6的两交点的距离即为EF的距离，
，
∴x2﹣6x+4＝0，
∴x1+x2＝6，x1•x2＝4，
∴EF＝ |x1﹣x2|＝2 ．
【分析】（1）①画出图即可直观求出点；②向上平移横坐标不变，纵坐标加m，再结合反比函数解析式联立方程求出m和k；（2）判断图象旋转后与直线相交的交点在直线上，而直线AB上点绕P点逆时针旋转后的轨迹是与AB垂直的直线，并且过A点，逆向思维，原反比例函数图象与轨迹直线的交点间距离就是EF距离．
50. （1）解：由正、反比例函数图象的对称性可知，点A、B关于原点O对称， 点的坐标为 ， 点的坐标为 ． 故答案为 ．
（2）解：①证明过程如下， 设 ，直线PA的解析式为 ． 则 ， 解得： ， 直线PA的解析式为 ． 当 时， ， 点的坐标为 ． 过点P作 轴于H，如图1所示， 点坐标为 ， 点的坐标为 ， ． 同理可得： ， ． ， ． 故答案为 ， ， ； ②由（2）①可知，在 中， ， 为等腰三角形，且 ． 当P点坐标为 时， ， ， ， ， ，即 ， 为直角三角形． 当 时，如图1， ， ， ， ； 当 时， ， ， ， ．
【分析】（1）根据正、反比例函数图象的对称性结合点A的坐标即可得出点B的坐标；（2）①设P（m， ），根据点P、A的坐标利用待定系数法可求出直线PA的解析式，利用一次函数图象上点的坐标特征可求出点M的坐标，过点P作PH⊥x轴于H，由点P的坐标可得出点H的坐标，进而即可求出MH的长度，同理可得出HN的长度，再根据等腰三角形的三线合一即可证出PM=PN；②根据①结合PH、MH、NH的长度，可得出△PAB为直角三角形，分k＞1和0＜k＜1两种情况，利用分割图形求面积法即可求出△PAB的面积．