吉林省延边州2023年数学六年级第二学期期末统考模拟试题含解析

吉林省延边州2023年数学六年级第二学期期末统考模拟试题

一、仔细填空。

1．（、都是非零自然数），和的最大公因数是（______），最小公倍数是（______）。

2．的分子加上6，要使分数的大小不变，分母应加上（______）。

3．小红从家去4km的图书馆看书，从统计图可以看出，她在图书馆看书用去_____分，去时的速度是每时_____km．

4．＝＝

5．下图是由边长为 2 厘米的 6 个小正方体堆起来的，那么这个图形的表面积是（___）平方厘米。

6．把三个棱长为3cm的正方体拼成一个长方体，那么棱长总和减少（________）cm，表面积减少了（________）cm2。

7．一桶水，当水成冰时，它的体积增加了，当冰化成水时，它的体积减少了.

8．一个方便袋里有30多个苹果，如果4个一盘或者6个一盘，正好分完．这个方便袋里共有（__________）个苹果．

9．一根长6米的铁丝，平均分成5段，每段占全长的（____），每段长（_____）米。

10．做一个长8分米，宽4分米，高3分米的无盖鱼缸，用角钢做它的框架，至少需要玻璃（______）dm³，最多可装水（______）L。

二、准确判断。（对的画“√ ”，错的画“×”）

11．把棱长4厘米的正方体，切成相等的两个长方体，每个长方体表面积是64平方厘米．（_____）

12．画折线统计图的第一步是画出横纵和纵轴    （_____）

13．要反映1个病人体温的变化情况，选用折线统计图比较合适。（______）

14．一个最简分数，分子与分母的乘积是20，这个最简分数只有一个。 （________）

15．半径是5厘米的圆比半径是2厘米的圆的圆周率大。 （____）

16．两个不同的非0自然数的最小公倍数一定是它们的最大公因数的倍数。（________）

三、谨慎选择。（将正确答案的标号填在括号里）

17．如果一个数恰好等于它的所有因数（本身除外）相加之和，那么这个数就是“完全数”。下列各数中，是“完全数”的是（    ）。

A．14 B．18 C．28 D．35

18．如果一个长方体的长扩大到原来的6倍，宽缩小到原来的，高不变，体积(  )．

A．缩小到原来的

B．扩大到原来的3倍

C．扩大到原来的2倍

D．不变

19．把一根绳子剪成两段，第一段长米，第二段占全长的，那么两段比较（   ）．

A．第一段长 B．第二段长 C．一样长 D．无法确定

20．下列图形中，不能围成正方体的是（    ）。

A． B． C．

21．与3.24÷1.2的商相等的算式是（    ）。

A．324÷12 B．32.4÷12 C．3.24÷12

四、细想快算。

22．直接写出得数：

+ =      + =        － =      

1－ =          -0.5=       + +=

23．用你喜欢的方法解答．

（1）10以内所有质数的和是多少？

（2）48与54的最大公约数乘以20以内的最大质数，积是多少？

24．看图列方程.并试着求出方程的解．

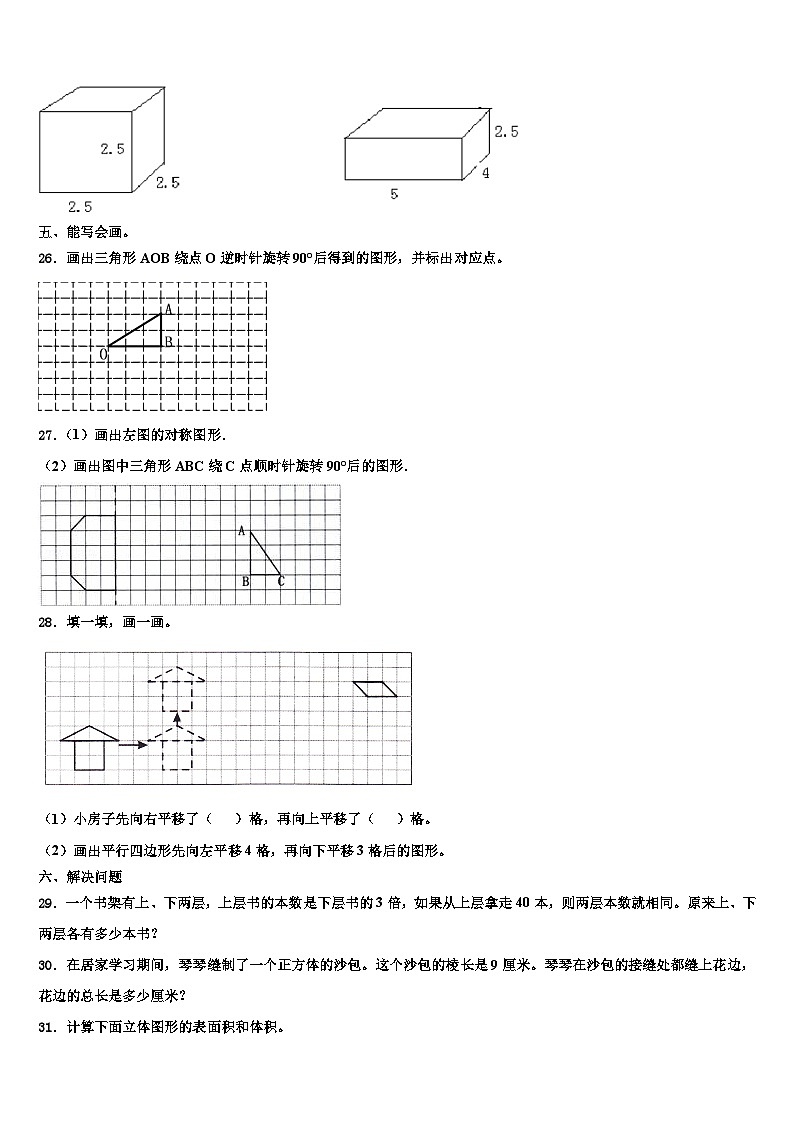
25．求下列图形的表面积和体积。（单位：厘米）

五、能写会画。

26．画出三角形AOB绕点O逆时针旋转90°后得到的图形，并标出对应点。

27．（1）画出左图的对称图形．

（2）画出图中三角形ABC绕C点顺时针旋转90°后的图形．

28．填一填，画一画。

（1）小房子先向右平移了（   ）格，再向上平移了（   ）格。

（2）画出平行四边形先向左平移4格，再向下平移3格后的图形。

六、解决问题

29．一个书架有上、下两层，上层书的本数是下层书的3倍，如果从上层拿走40本，则两层本数就相同。原来上、下两层各有多少本书？

30．在居家学习期间，琴琴缝制了一个正方体的沙包。这个沙包的棱长是9厘米。琴琴在沙包的接缝处都缝上花边，花边的总长是多少厘米？

31．计算下面立体图形的表面积和体积。

1.

2.底面是周长为8分米的正方形

32．有一批煤,第一天用去t，第二天比第一天少用去t，两天一共用去多少吨煤？

33．解方程．

3.6x÷2=2.16       2x－1.5x＝1.9        ＋x＝          0.9x－3×1.2=7.2

参考答案

一、仔细填空。

1、       

【分析】根据（、都是非零自然数），说明m是n的8倍；当两个数有倍数关系时，它们的最大公因数是较小数，最小公倍数是较大数。

【详解】由分析可得，和的最大公因数是，最小公倍数是。

故答案为：；

此题考查求两个数有倍数和因数关系时的最大公因数和最小公倍数的方法，要熟练掌握。

2、14

【解析】略

3、70    1   

【解析】（1）由统计图的水平线的起止时间相减即可得到在图书馆看书的时间．

（2）运用路程4千米除以时间（30分钟=0.5小时）等于速度即可进行计算．

【详解】（1）在图书馆看书的时间：

100﹣30=70（分钟）

答：她在图书馆看书用去70分．

（2）去时的速度是：

4÷（30÷60）

=1（千米）

答：去时的速度是每时1km．

故答案为70，1．

4、8；15

【分析】根据分数的基本性质，从已知的入手，3到12扩大几倍，2就扩大几倍；2到10扩大几倍，3就扩大几倍，据此分析。

【详解】12÷3×2＝8；10÷2×3＝15

＝＝

本题考查了分数的基本性质，分数的分子和分母同时乘或除以相同的数（0除外），分数的大小不变。

5、96

【解析】略

6、48    36   

【分析】如图，棱长总和减少了4×4条小正方体的棱长；表面积减少了4个小正方形。

【详解】3×4×4＝48（厘米）

3×3×4＝36（平方厘米）

本题考查了立体图形的拼组，正方体有6个面，都是完全一样的正方形。

7、

【解析】略

8、36

【解析】略

9、       

【详解】略

10、104    96   

【分析】求需要的玻璃就是求没有上面的长方体表面积，依据公式：S＝ab＋2ah＋2bh；求盛水多少升就是求长方体容积，依据公式：V＝abh；据此列式计算。

【详解】需要玻璃：8×4＋8×3×2＋4×3×2

＝32＋48＋24

＝104（平方分米）

最多可装水：8×4×3＝96（立方分米）

96立方分米＝96升

本题考查了长方体的表面积和体积，很多时候求无上面或下面的表面积，还有贴商标只求前后左右4个面的面积和。

二、准确判断。（对的画“√ ”，错的画“×”）

11、√

【解析】4×4×（6+2）÷2＝4×4×8÷2＝128÷2＝64（平方厘米）．

答：每个长方体表面积是64平方厘米．

故答案为√．

12、错误

【解析】是整理数据

【分析】考察了复式折线统计图的解决能力

13、√

【分析】折线统计图：用不同位置的点表示数量的多少，并用折线的上升和下降表示数量的增减变化情况，据此解答。

【详解】要反映1个病人体温的变化情况，选用折线统计图比较合适。这种说法是正确的。

故答案为：√

折线统计图优点：折线统计图不仅能表示出数量的多少，还能反映出数量的变化情况。

14、╳

【解析】略

15、×

【解析】略

16、√

【分析】求两个数的最大公因数、最小公倍数，把两个数分别分解质因数，公有质因数的积就是最大公因数，公有质因数和各自质因数的连乘积就是最小公倍数；据此解答。

【详解】由分析可知：两数的最大公因数是共有质因数的乘积，最小公倍数是公有质因数和各自质因数的连乘积，所以两个不同的非0自然数的最小公倍数一定是它们的最大公因数的倍数。

故答案为：√

本题主要考查对最大公因数、最小公倍数的理解，解题时要明确：用分解质因数的方法求最大公因数、最小公倍数时，两数的最大公因数是共有质因数的乘积，最小公倍数是公有质因数和各自质因数的连乘积。

三、谨慎选择。（将正确答案的标号填在括号里）

17、C

【分析】根据完全数的定义，可将下列选项中的数字进行计算，即可得出答案。

【详解】A.14的因数有：1、2、7、14，所以1＋2＋7＝10；

B.18的因数有：1、2、3、6、9、18，所以1＋2＋3＋6＋9＝21，

C.28的因数有：1、2、4、7、14、28，所以1＋2＋4＋7＋14＝28；

D．35的因数有：1、5、7、35，所以1＋5＋7＝13。

故答案为：C。

本题主要考查求一个数的因数的方法，注意完全数的意义：如果一个数恰好等于它的所有因数（本身除外）相加之和，那么这个数就是“完全数”。

18、C

【解析】略

19、A

【详解】第二段占全长的，说明第一段占，＞．故第一段长 选A.

20、A

【分析】根据正方体11种展开图进行分析。

【详解】A． ，不能围成正方体；

B． ，1－4－1型，能围成正方体；

C． ，2－3－1型，能围成正方体。

故答案为：A

本题考查了正方体展开图，要牢记11种展开图，或有较强的空间想象能力。

21、B

【分析】商不变的性质：被除数和除数同时乘或除以相同的数（0除外），商不变；由此可知与3.24÷1.2的商相等的算式是32.4÷12；据此解答。

【详解】根据商不变的性质可得：

3.24÷1.2

＝（3.24×10）÷（1.2×10）

＝32.4÷12

故答案为：B

本题考查了小数除法，关键是要掌握商不变的性质。

四、细想快算。

22、     

【详解】略

23、（1）17；（2）114

【分析】（1）10以内的质数有：2、3、5、7，求和即可

（2）用短除法求出48与54的最大公约数，再乘以20以内最大质数19即可。

【详解】（1）2+3+5+7=17

（2）6×19=114

本题主要考查20以内的质数及用短除法求最大公约数的方法，注意计算过程中要细心．

24、51

【详解】4X＋68=272   X=51

25、（1）正方体表面积：37.5平方厘米；正方体体积：15.625立方厘米

（2）长方体表面积：85平方厘米；长方体体积：50立方厘米

【分析】根据正方体和长方体的表面积和体积公式计算即可。

【详解】（1）正方体表面积：

2.5×2.5×6

＝6.25×6

＝37.5（平方厘米）

正方体体积：

2.5×2.5×2.5

＝6.25×2.5

＝15.625（立方厘米）

（2）长方体表面积：

（5×4＋4×2.5＋5×2.5）×2

＝（20＋10＋12.5）×2

＝42.5×2

＝85（平方厘米）

长方体体积：

5×4×2.5

＝20×2.5

＝50（立方厘米 ）

故答案为：（1）正方体表面积：37.5平方厘米；正方体体积：15.625立方厘米；（2）长方体表面积：85平方厘米；长方体体积：50立方厘米。

本题考查长方体、正方体的表面积和体积，须熟记长方体、正方体的表面积和体积的计算公式。

五、能写会画。

26、

【解析】略

27、（1）画出左图的对称图形（下图）：

（2）画出图中三角形ABC绕C点顺时针旋转90°后的图形（下图）：

【解析】（1）根据轴对称图形的特征，对称点到对称轴的距离相等，对称点的连线垂直于对称轴，在对称轴的右边画出左半图的关键对称点，依次连结即可．

（2）根据旋转的特征，三角形ABC绕点C顺时针旋转90°后，点C的位置不动，其余各部分均绕此点按相同方向旋转相同的度数，即可画出旋转后的图形．

28、（1）6   4

（2）

【解析】略

六、解决问题

29、上层60本；下层20本

【分析】设下层原来有x本书，则上层原来有3x本书，根据上层本数－40＝下层本数，列方程求解即可。

【详解】解：设下层原来有x本书，则上层原来有3x本书，根据题意得：

3x－40＝x

2x＝40

x＝20

3x＝3×20＝60

答：原来上层有60本书，下层有20本书。

通过设未知数，根据题目中所给和条件列出等量关系式是完成本题的关键。

30、108厘米

【分析】花边的总长就是正方体的棱长之和。正方体有12条棱，长度都相等，用棱长乘12即可求出棱长之和。

【详解】9×12＝108（厘米）

答：花边的总长是108厘米。

本题考查正方体有关棱长的应用，根据正方体棱长的特点即可解答。

31、1.表面积：5×5×6＝150(平方分米)

体积：5×5×5＝115(立方分米)

1．表面积：8÷4＝1(分米)

1×1×1＋1×6×4＝56(平方分米)

体积：1×1×6＝14(立方分米)

【解析】略

32、 - + =（t）

【解析】略

33、1.2  3.8      12

【解析】略