2022高考数学选填经典题型汇编 题型3 函数的奇偶性、对称性、周期性

题型3   函数的奇偶性、对称性、周期性

【方法点拨】

1.常见的与周期函数有关的结论如下：

(1)如果f(x＋a)＝－f(x)(a≠0)，那么f(x)是周期函数，其中的一个周期T＝2a.

(2)如果f(x＋a)＝(a≠0)，那么f(x)是周期函数，其中的一个周期T＝2a.

(3)如果f(x＋a)＋f(x)＝c(a≠0)，那么f(x)是周期函数，其中的一个周期T＝2a.

2.函数奇偶性、对称性间关系：

(1)若函数y＝f(x＋a)是偶函数，即f(a＋x)＝f(a－x)恒成立，则y＝f(x)的图象关于直线x＝a 对称；一般的，若f(a＋x)＝f(b－x)恒成立，则y＝f(x)的图象关于直线x＝对称．

(2)若函数y＝f(x＋a)是奇函数，即f(－x＋a)＋f(x＋a)＝0恒成立，则函数y＝f(x)关于点(a，0)中心对称；一般的，若对于R上的任意x都有f(a＋x)＋f(a－x)＝2b恒成立，则y＝f(x)的图象关于点(a，b)对称.

3. 函数对称性、周期性间关系：

若函数有多重对称性，则该函数具有周期性且最小正周期为相邻对称轴距离的2倍，为相邻对称中心距离的2倍，为对称轴与其相邻对称中心距离的4倍．

(注：如果遇到抽象函数给出类似性质，可以联想y＝sinx，y＝cosx的对称轴、对称中心和周期之间的关系)

4. 善于发现函数的对称性（中心对称、轴对称），有时需将对称性与函数的奇偶性相互转化.

【典型题示例】

例1   （2021·新高考全国Ⅱ卷·8）已知函数的定义域为，为偶函数，为奇函数，则（    ）

A.  B.  C.  D.

【答案】B

【分析】推导出函数是以为周期的周期函数，由已知条件得出，结合已知条件可得出结论.

【解析】因为函数为偶函数，则，可得，

因为函数为奇函数，则，所以，，

所以，，即，

故函数是以为周期的周期函数，

因为函数为奇函数，则，

故，其它三个选项未知.

故选：B.

例2   （2021·全国甲卷（理）·12）设函数的定义域为R，为奇函数，为偶函数，当时，．若，则（    ）

A.  B.  C.  D.

【答案】D

【分析】通过是奇函数和是偶函数条件，可以确定出函数解析式，进而利用定义或周期性结论，即可得到答案．

【解析】因为是奇函数，所以①；

因为是偶函数，所以②．

令，由①得：，由②得：，

因为，所以，

令，由①得：，所以．

思路一：从定义入手．

所以．

思路二：从周期性入手

由两个对称性可知，函数的周期．

所以．

故选：D．

例3    已知函数f (x)对任意的x∈R，都有f ＝f ，函数f (x＋1)是奇函数，当－≤x≤时，f (x)＝2x，则方程f (x)＝－在区间[－3,5]内的所有根之和为________.

【答案】4

【分析】由f ＝f 对任意的x∈R恒成立，得f (x)关于直线x＝对称，由函数

f (x＋1)是奇函数，f (x)关于点（1,0）中心对称，根据函数对称性、周期性间关系，知函数f (x)的周期为2，作出函数f (x)的图象即可.

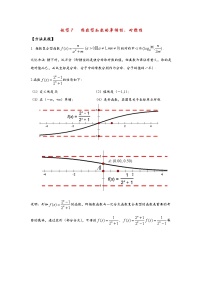
【解析】因为函数f (x＋1)是奇函数，所以f (－x＋1)＝－f (x＋1)，又因为f ＝ f ，所以f (1－x)＝f (x)，所以f (x＋1)＝－f (x)，即f (x＋2)＝－f (x＋1)＝f (x)， 所以 函数f (x)的周期为2，且图象关于直线x＝对称．作出函数f (x)的图象如图所示，

由图象可得f (x)＝－在区间[－3,5]内有8个零点，且所有根之和为×2×4＝4.

例4    已知是定义域为的奇函数，满足．若，则

A．    B．0    C．2    D．50

【答案】C

【分析】同例1得f (x)的周期为4，故f (1) ＋f (2) ＋f (3) ＋f (4)＝f (5) ＋f (6) ＋f (7) ＋f (8) ＝···＝f (45) ＋f (46) ＋f (47) ＋f (48)，而f (1)＝2，f (2)＝f (0)＝0（f(1－x)＝f(1＋x)中，取x＝1）、f (3)＝f (－1) ＝－f (1)＝－2、f (4)＝f (0)＝0，故f (1) ＋f (2) ＋f (3) ＋f (4)＝f (5) ＋f (6) ＋f (7) ＋f (8) ＝···＝f (45) ＋f (46) ＋f (47) ＋f (48) ＝0，所以f (1) ＋f (2) ＋f (3) ＋···＋f (50) ＝f (47) ＋f (48) ＝f (1) ＋f (2) ＝2.

例5    已知函数是上的奇函数，对任意，都有（2）成立，当，，，且时，都有，则下列结论正确的有　　

A．（1）（2）（3） 

B．直线是函数图象的一条对称轴 

C．函数在，上有5个零点 

D．函数在，上为减函数

【分析】根据题意，利用特殊值法求出（2）的值，进而分析可得是函数的一条对称轴，函数是周期为4的周期函数和在区间，上为增函数，据此分析选项即可得答案．

【解答】解：根据题意，函数是上的奇函数，则；

对任意，都有（2）成立，当时，有（2），则有（2），

则有，即是函数的一条对称轴；

又由为奇函数，则，变形可得，则有，

故函数是周期为4的周期函数，

当，，，且时，都有，则函数在区间，上为增函数，

又由是上的奇函数，则在区间，上为增函数；

据此分析选项：

对于，，则（1）（2）（3）（4）（1）（3） （2）（4），

（1）（2）（3）（1）（2）（3）（4） （1）（2）（3）（2），正确；

对于，是函数的一条对称轴，且函数是周期为4的周期函数，则 是函数的一条对称轴，

又由函数为奇函数，则直线是函数图象的一条对称轴，正确；

对于，函数在，上有7个零点：分别为，，，0，2，4，6；错误；

对于，在区间，上为增函数且其周期为4，函数在，上为增函数，

又由为函数图象的一条对称轴，则函数在，上为减函数， 正确；

故选：．

【巩固训练】

1．已知函数关于对称,则的解集为_____.

2．已知定义在上的函数满足，且的图象与的图象有四个交点，则这四个交点的横纵坐标之和等于___________.

3.已知函数满足，且时，，则（    ）

A．0 B．1 C． D．

4. 已知f(x)是定义域为R的函数，满足f(x＋1)＝f(x－3)，f(1＋x)＝f(3－x)，当0≤x≤2时，f(x)＝x2－x，则下列说法正确的是(　　)

A.函数f(x)的周期为4

B.函数f(x)图象关于直线x＝2对称

C.当0≤x≤4时，函数f(x)的最大值为2

D.当6≤x≤8时，函数f(x)的最小值为－

5.已知定义在R上的奇函数，满足，且在区间[0，2]上是增函数，若方程f(x)=m(m>0)在区间上有四个不同的根，则   8

6．(多选题)函数f(x)的定义域为R，且f(x＋1)与f(x＋2)都为奇函数，则(　　)

A.f(x)为奇函数    B.f(x)为周期函数

C.f(x＋3)为奇函数    D.f(x＋4)为偶函数

7.若定义在R上的函数满足，是奇函数，现给出下列4个论断：

①是周期为4的周期函数；②的图象关于点对称；

③是偶函数；            ④的图象经过点；

其中正确论断的个数是______________.

8. (多选题)已知定义在R上的函数f(x)满足f(x)＝2－f(2－x)，且f(x)是偶函数，下列说法正确的是(　　)

A.f(x)的图象关于点(1，1)对称                              B.f(x)是周期为4的函数

C.若f(x)满足对任意的x∈[0，1]，都有<0，则f(x)在[－3，－2]上单调递增

D.若f(x)在[1，2]上的解析式为f(x)＝ln x＋1，则f(x)在[2，3]上的解析式为f(x)＝1－ln(x－2)

【答案与提示】

1．【答案】

【解析】∵函数关于对称,∴,

则由,结合图象可得,求得.

2．【答案】8

【解析】，故，即的图象关于点对称，又函数满足，则函数的图象关于点对称，所以四个交点的横纵坐标之和为8.

3. 【答案】D

【解析】因为，

所以

.

4. 【答案】ABC

【解析】　由f(x＋1)＝f(x－3)，得f(x)＝f[(x－1)＋1]＝f[(x－1)－3]＝f(x－4)，所以函数f(x)的周期为4，A正确.由f(1＋x)＝f(3－x)，得f(2＋x)＝f(2－x)，所以函数f(x)的图象关于直线x＝2对称，B正确.当0≤x≤2时，函数f(x)在上单调递减，在上单调递增.所以当x＝时，函数f(x)在[0，2]上取得极小值－，且f(0)＝0，f(2)＝2.作出函数f(x)在[0，8]上的大致图象，如图.由图可知，当0≤x≤4时，函数f(x)的最大值为f(2)＝2，C正确；当6≤x≤8时，函数f(x)的最小值为f＝f＝－，D错误.故选ABC.

5.  8【答案】－8

【提示】四个根分别关于直线，对称.

6．【答案】ABC

【解析】法一　由f(x＋1)与f(x＋2)都为奇函数知，函数f(x)的图象关于点(1，0)，(2，0)对称，所以f(－x)＋f(2＋x)＝0，f(－x)＋f(4＋x)＝0，所以f(2＋x)＝f(4＋x)，即f(x)＝f(2＋x)，所以f(x)是以2为周期的周期函数.又f(x＋1)与f(x＋2)都为奇函数，所以f(x)，f(x＋3)，f(x＋4)均为奇函数.故选ABC.

法二　由f(x＋1)与f(x＋2)都为奇函数知，函数f(x)的图象关于点(1，0)，(2，0)对称，所以f(x)的周期为2|2－1|＝2，所以f(x)与f(x＋2)，f(x＋4)的奇偶性相同，f(x＋1)与f(x＋3)的奇偶性相同，所以f(x)，f(x＋3)，f(x＋4)均为奇函数.故选ABC.

7.【答案】3

【解析】命题①：由，得：，

所以函数的周期为4，故①正确；

命题②：由是奇函数，知的图象关于原点对称，

所以函数的图象关于点对称，故②正确；

命题③：由是奇函数，得：，

又，

所以，

所以函数是偶函数，故③正确；

命题④：，

无法判断其值，故④错误.综上，正确论断的序号是：①②③.

8. 【答案】ABC

【解析】根据题意，f(x)的图象关于点(1，1)对称，A正确；又f(x)的图象关于y轴对称，所以f(x)＝f(－x)，则2－f(2－x)＝f(－x)，f(x)＝2－f(x＋2)，从而f(x＋2)＝2－f(x＋4)，所以f(x)＝f(x＋4)，B正确；由<0可知f(x)在[0，1]上单调递增，又f(x)的图象关于点(1，1)对称，所以f(x)在[1，2]上单调递增，因为f(x)的周期为4，所以f(x)在[－3，－2]上单调递增，C正确；因为f(x)＝f(－x)，x∈

[－2，－1]时，－x∈[1，2]，所以f(x)＝f(－x)＝ln(－x)＋1，x∈[－2，－1]，因为f(x)的周期为4，f(x)＝f(x－4)，x∈[2，3]时，x－4∈[－2，－1]，所以f(x)＝f(x－4)＝ln(4－x)＋1，x∈[2，3]，D错误.综上，正确的是ABC.