北师大版二年级数学上册暑假预习与检测衔接讲义

第4单元 图形的变化

1、轴对称图形

一个图形对折后，折痕两边的部分能够完全重合，这样的图形就是轴对称图形。

2、平移

物体或图形沿着直线运动的现象叫平移。

3、旋转

物体或图形绕着一个轴或一个点进行圆周运动的现象叫旋转。

【例1】下面哪些图形是轴对称图形？在括号里画“√”

【分析】根据轴对称图形的意义：如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴；由此解答即可。

【解答】解：根据轴对称图形的意义，解答如下：

【点评】此题考查了轴对称图形的意义，判断轴对称图形的关键是寻找对称轴，看图形对折后两部分是否完全重合。

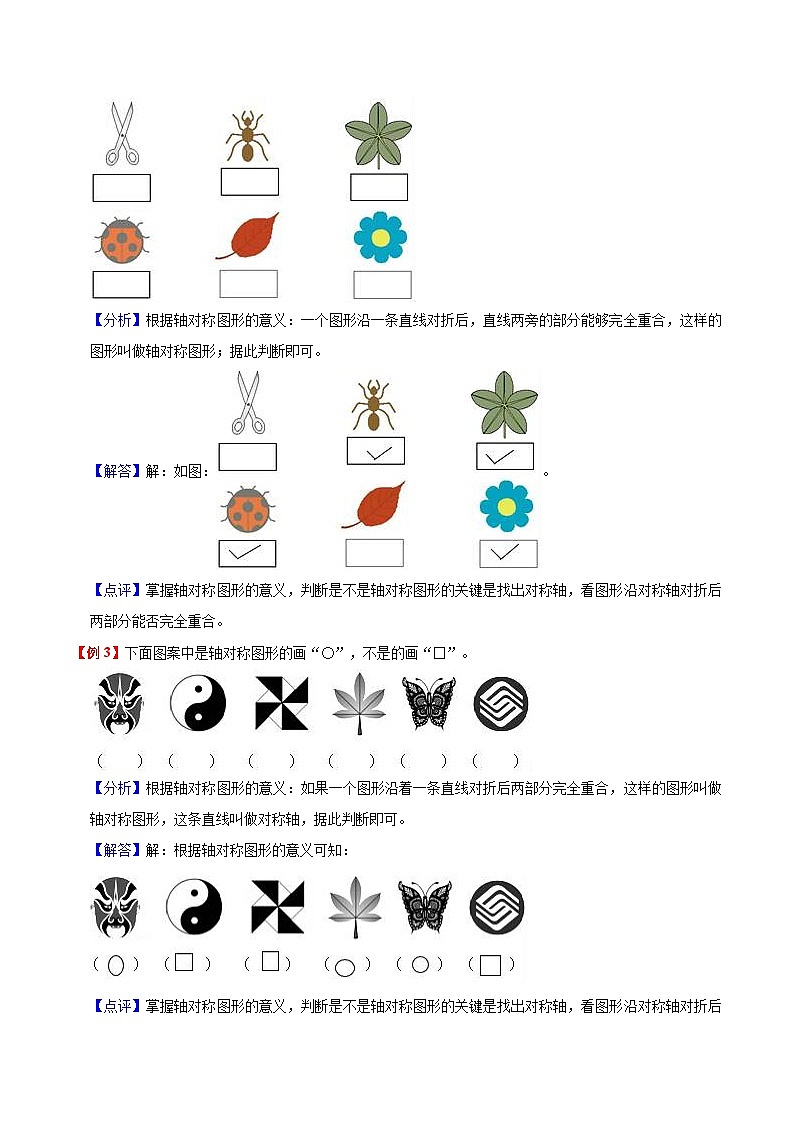
【例2】找一找，哪些是对称的。（对称的在方框里打“√”）

【分析】根据轴对称图形的意义：一个图形沿一条直线对折后，直线两旁的部分能够完全重合，这样的图形叫做轴对称图形；据此判断即可。

【解答】解：如图：。

【点评】掌握轴对称图形的意义，判断是不是轴对称图形的关键是找出对称轴，看图形沿对称轴对折后两部分能否完全重合。

【例3】下面图案中是轴对称图形的画“〇”，不是的画“□”。

【分析】根据轴对称图形的意义：如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴，据此判断即可。

【解答】解：根据轴对称图形的意义可知：

【点评】掌握轴对称图形的意义，判断是不是轴对称图形的关键是找出对称轴，看图形沿对称轴对折后两部分能否完全重合。

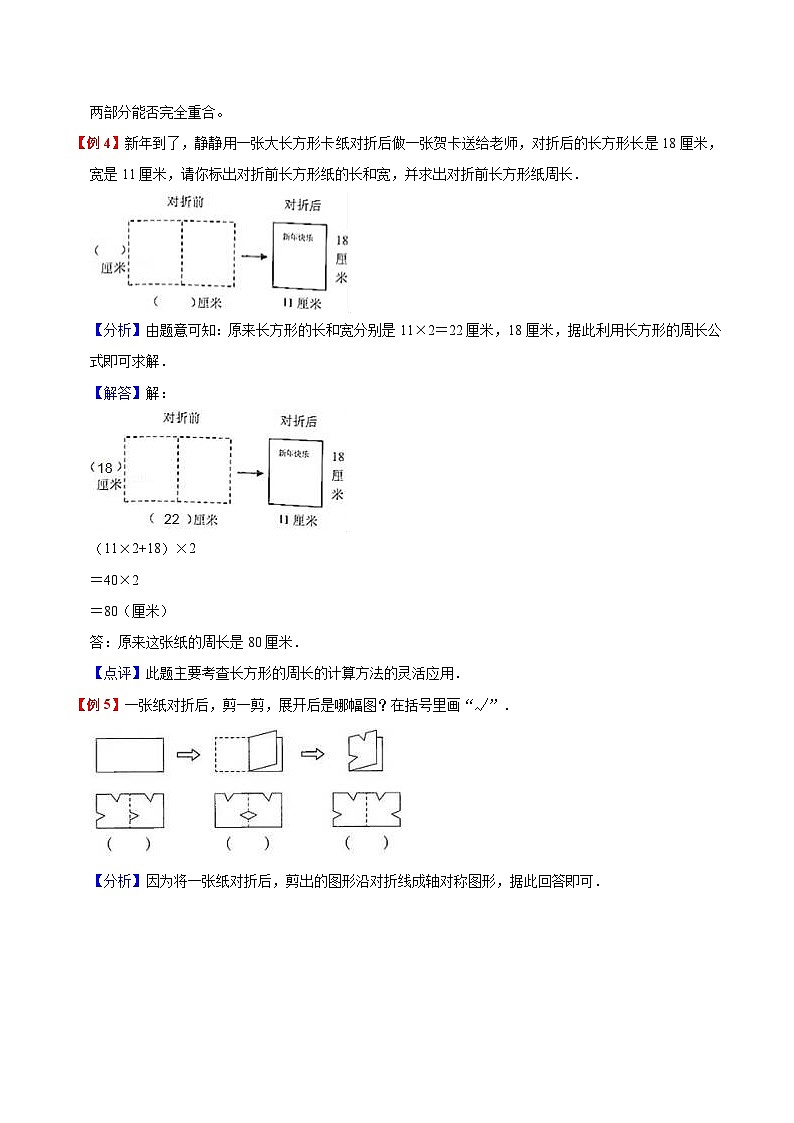
【例4】新年到了，静静用一张大长方形卡纸对折后做一张贺卡送给老师，对折后的长方形长是18厘米，宽是11厘米，请你标出对折前长方形纸的长和宽，并求出对折前长方形纸周长．

【分析】由题意可知：原来长方形的长和宽分别是11×2＝22厘米，18厘米，据此利用长方形的周长公式即可求解．

【解答】解：

（11×2+18）×2

＝40×2

＝80（厘米）

答：原来这张纸的周长是80厘米．

【点评】此题主要考查长方形的周长的计算方法的灵活应用．

【例5】一张纸对折后，剪一剪，展开后是哪幅图？在括号里画“√”．

【分析】因为将一张纸对折后，剪出的图形沿对折线成轴对称图形，据此回答即可．

【解答】解：

【点评】解决本题的关键是明确将一张纸对折后，剪出的图形沿对折线成轴对称图形．

一．选择题（共8小题）

1．如图，将一张正方形纸对折后，沿虚线剪下一个小正方形，剩下的部分打开后是（　　）

A． B． C．

2．下面的图案是轴对称图形的有（　　）个。

A．1 B．2 C．3

3．如图展开后的图形是（　　）

A． B． C．

4．下面不是轴对称图形的是（　　）

A． B． C．

5．图中，（　　）不是轴对称图形。

A． B． 

C．

6．将一张长方形纸对折后，沿虚线剪开，剪出的图形展开后是（　　）

A． B． 

C．

7．下列英文字母中，是轴对称图形的是（　　）。

A．S B．H C．Q

8．如图所示，王红把一张正方形纸这样折叠4次，再沿虚线剪一刀，打开后的图形接近（　　）

A．三角形 B．圆 C．正方形

二．填空题（共8小题）

9．一张正方形纸对折一次，可能折出两个　   　形，也可能折出两个　   　形。

10．如图的两个图形中，图 　 　是轴对称图形。

11．在数字6、8和9中，数字　 　是轴对称图形。

12．在CHINA中，是轴对称图形的字母有　 　个。

13．芳芳把一张正方形的纸对折了一次，她折出的图形可能是　   　形或　   　形。

14．将等边三角形纸片按如图所示步骤折叠3次（图1中的虚线是三边中点的连线），然后沿过两边的中点的直线剪去一角（如图2）．

将剩下的纸片展开，平铺，得到的图形是　 　．

15．如图图形，有　 　个轴对称图形。

16．一根绳子对折、对折、对折、再对折，从中间剪开，绳子分成　   　段．

三．判断题（共5小题）

17．是轴对称图形。　 　（判断对错）

18．0和8是轴对称图形。　 　（判断对错）

19．左边的扑克牌是轴对称图形。　 　（判断对错）

20．是轴对称图形。　 　（判断对错）

21．一根绳子长20米，对折两次后，每段长10米。　 　（判断对错）

四．应用题（共1小题）

22．小明做折纸的游戏，一张纸第一次对折，得纸2层，第二次对折，得纸4层，如此下去，第五次对折得纸多少层？

五．操作题（共4小题）

23．它们沿虚线折出来是什么样子？连一连。

24．连一连。

25．下面这些图形是轴对称图形，是轴对称图形的画△．

26．下图中是轴对称的画“√”，不是的画“×”。

六．解答题（共2小题）

27．折折剪剪动手操作一张正方形纸片，通过两次对折，然后按照阴影部分进行裁剪并展开，可以得到如图1末的蝴蝶结：请模仿图1，讲下面的正方形纸片经过两次对折裁剪并展开，得到图2末的图形，请画出虚线和实线表示折叠过程，并用阴影表示剪去的部分．

28．像下面（图1）这样把一张纸连续对折3次，剪出来的是什么图案？

在下面（图2）对应的图案上打“√”．

参考答案与试题解析

一．选择题（共8小题）

1．【分析】一张正方形对折后，沿着虚线剪下一个小正方形，剩下的部分打开，正方形里面是一个小长方形。

【解答】解：将一张正方形纸对折后，沿虚线剪下一个小正方形，剩下的部分打开后是，如下图：

故选：B。

【点评】此题可动手操作一下．关键是注意折叠的方向和剪下的图形。

2．【分析】根据轴对称图形的意义：如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴；依次进行解答即可。

【解答】解：根据轴对称图形的意义可知：在上面给出的4个图形中，后面2个是轴对称图形，前两个不是轴对称图形。

故选：B。

【点评】此题考查了轴对称图形的意义，判断轴对称图形的关键是寻找对称轴，看图形对折后两部分是否完全重合。

3．【分析】根据轴对称图形的意义：如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴；据此解答即可。

【解答】解：如图展开后的图形是。

故选：B。

【点评】掌握轴对称图形的意义，判断是不是轴对称图形的关键是找出对称轴，看图形沿对称轴对折后两部分能否完全重合。

4．【分析】据轴对称图形的概念，即在平面内，如果一个图形沿一条直线折叠，直线两旁的部分能够完全重合，这样的图形叫做轴对称图形，这条直线就是这个轴对称图形的对称轴，据此即可解答。

【解答】解：圆和正方形都是轴对称图形，平行四边形不是轴对称图形。

故选：B。

【点评】掌握轴对称图形的意义，判断是不是轴对称图形的关键是找出对称轴，看图形沿对称轴对折后两部分能否完全重合。

5．【分析】一个图形沿着一条直线对折，直线两边的图形能够完全重合，这样的图形叫做轴对称图形；据此判断即可。

【解答】解：根据轴对称图形的定义可得：不是轴对称图形。

故选：C。

【点评】此题主要考查轴对称图形的定义及实际应用。

6．【分析】将一张长方形纸对折后，沿虚线剪开，剪出的图形是轴对称图形，图形两边能完全重合。剪开后是一个等腰三角形。

【解答】解：将一张长方形纸对折后，沿虚线剪开，剪出的图形展开后是等腰三角形。

故选：B。

【点评】本题是考查简单图形的折叠问题，折叠后的图形是轴对称图形。

7．【分析】根据轴对称图形的意义：如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴；依次进行判断即可。

【解答】解：“H”是轴对称图形。S和Q都不是轴对称图形。

故选：B。

【点评】此题考查了轴对称图形的意义，判断轴对称图形的关键是寻找对称轴，看图形对折后两部分是否完全重合。

8．【分析】根据王红的做法可知，把一张正方形纸这样折叠4次，再沿虚线剪一刀，打开后的图形接近圆，这是因为正多边形边数越多越接近圆。据此解答。

【解答】解：王红把一张正方形纸这样折叠4次，再沿虚线剪一刀，打开后的图形接近圆。

故选：B。

【点评】本题主要考查图形的折叠问题，解决本题的思想是圆的周长公式的推导。

二．填空题（共8小题）

9．【分析】一个正方形沿对边中点连线对折一次后，可得到2个长为原正方形边长，宽为原正方形边长一半的长方形；把一个正方形沿对角线对折一次，可得到2个两直角边为原正方形边长的等腰直角三角形；据此解答即可。

【解答】解：一张正方形纸对折一次，可能折出两个长方形，也可能折出两个三角形。

故答案为：长方；三角。

【点评】本题考查了简单图形的折叠问题，要有一定的空间想象能力。

10．【分析】根据轴对称图形的意义：如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴；由此解答即可。

【解答】解：如图的两个图形中，图1是轴对称图形。

故答案为：1。

【点评】此题考查了轴对称图形的意义，判断轴对称图形的关键是寻找对称轴，看图形对折后两部分是否完全重合。

11．【分析】依据轴对称图形的概念，即在平面内，如果一个图形沿一条直线折叠，直线两旁的部分能够完全重合，这样的图形叫做轴对称图形，这条直线就是这个轴对称图形的对称轴，据此即可解答。

【解答】解：在数字6、8和9中，数字8是轴对称图形。

故答案为：8。

【点评】掌握轴对称图形的意义，判断是不是轴对称图形的关键是找出对称轴，看图形沿对称轴对折后两部分能否完全重合。

12．【分析】根据轴对称图形的意义：如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴；依次进行判断即可。

【解答】解：在CHINA中，CHIA是轴对称图形，是轴对称图形的字母有4个。

故答案为：4。

【点评】此题考查了轴对称图形的意义，判断轴对称图形的关键是寻找对称轴，看图形对折后两部分是否完全重合。

13．【分析】一个正方形沿对边中点连线对折一次后，可得到2个长为原正方形边长，宽为原正方形边长一半的长方形；把一个正形沿对角线对折一次，可得到2个两直角边为原正方形边长的等腰直角三角形；据此解答即可。

【解答】解：芳芳把一张正方形的纸对折了一次，她折出的图形可能是长方形或三角形。

故答案为：长方；三角。

【点评】本题是考查简单图形的折叠问题，要有一定的空间想象能力。

14．【分析】找一个等边三角形纸片按图中所示步骤折叠3次，然后用剪刀沿两边的中点的直线剪去一角，将剩下的纸片展开、平铺看一看，即可得出答案．

【解答】解：找一剪刀与一等边三角形纸片，按题中所示步骤进行操作，

最后得到的图形是丁；

故答案为：丁．

【点评】解答此题的关键是，根据所给的步骤，进行实际操作，即可得出答案．

15．【分析】一个图形沿着一条直线对折，直线两边的图形能够完全重合，这样的图形叫做轴对称图形；据此解答即可。

【解答】解：图①、②、④、⑤沿一条直线对折后，直线两旁的部分能够互相重合，所以图①、②、④、⑤是轴对称图形；

图③无论沿哪一条直线对折后，直线两旁的部分都不能够互相重合，所以它不是轴对称图形；

所以有4个轴对称图形。

故答案为：4。

【点评】此题主要考查轴对称图形的定义及应用。

16．【分析】首先从最简单情况开始考虑：不对折，从中间剪开，2段；第一次对折后，剪开，是3段（2+1）；第二次对折后，剪开，是5段（2+1+2）；…找出规律，解答问题．

【解答】解：不对折，从中间剪开，2段；

第一次对折后，剪开，是3段（2+1）；

第二次对折后，剪开，是5段（2+1+2）；

第三次对折后，剪开，是9段（2+1+2+4）；

第四次对折后，剪开，是17段（2+1+2+4+8）；

故答案为17．

【点评】此题属于简单的图形操作题，可以动手做一下得出答案，也可以数剪开之后绳子的头数即可：一根绳子2个头，剪开4个头（不对折），对折一次剪开6个头，对折两次剪开10个头…找出规律进行解答．

三．判断题（共5小题）

17．【分析】依据轴对称图形的定义及特征即可作答：一个图形沿某条直线对折，直线两旁的部分能够完全重合，这个图形就是轴对称图形，这条直线就是这个图形的一条对称轴；由此解答即可。

【解答】解：根据轴对称图形的含义可知：不是轴对称图形，所以本题说法错误。

故答案为：×。

【点评】明确轴对称图形的含义，是解答此题的关键。

18．【分析】根据轴对称图形的意义：如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴，由此进行解答即可。

【解答】解：0和8是轴对称图形，说法正确。

故答案为：√。

【点评】此题考查了轴对称图形的意义，判断轴对称图形的关键是寻找对称轴，看图形对折后两部分是否完全重合。

19．【分析】根据轴对称图形的定义：如果一个图形沿某条直线对折，直线两旁的部分能够完全重合，这个图形就是轴对称图形，这条直线就是它的一条对称轴，据此即可解答问题。

【解答】解：左边的扑克牌不是轴对称图形，故原题说法错误。

故答案为：×。

【点评】此题考查了轴对称图形的意义，判断轴对称图形的关键是寻找对称轴，看图形对折后两部分是否完全重合。

20．【分析】依据轴对称图形的意义，即在平面内，如果一个图形沿一条直线对折，对折后的两部分都能完全重合，这样的图形叫做轴对称图形，据此即可进行解答。

【解答】解：是轴对称图形，符合轴对称图形的意义，所以说法正确。

故答案为：√。

【点评】此题主要考查轴对称图形的定义。

21．【分析】把这条20米长的绳子对折一次，被平均分成2段，对折两次，被平均分成4段，求每段长，根据整数除法的意义即可解答，再根据计算结果作出判断。

【解答】解：一根绳子长20米，对折两次后，被平均分成4段

20÷4＝5（米）

一根绳子长20米，对折两次后，每段长5米。

原题说法错误。

故答案为：×。

【点评】解答此题的关键是弄清这根绳子对折两次，被平均分成了几段，然后再根据表内除法解答。

四．应用题（共1小题）

22．【分析】根据折叠规律，每对折一次层数扩大2倍，第五次对折得纸25层，计算即可．

【解答】解：25＝32（层）

答：第五次对折得纸32层．

【点评】解答本题关键是明确对折n次，层数变成了2n层．

五．操作题（共4小题）

23．【分析】正方形沿着对角线对折之后得到三角形。圆形沿着直径对折后得到半圆。正方形对折两次后，就相当于把正方形平均分成了4份，折出的图形的形状，就是每份的形状。

【解答】解：

【点评】本题主要考查学生的动手能力及空间想象能力。还要结合所学的平面图形的特点进行分析。

24．【分析】依据轴对称图形的意义，即在平面内，如果一个图形沿一条直线对折，对折后的两部分都能完全重合，这样的图形叫做轴对称图形，据此即可进行连线。

【解答】解：

【点评】此题考查了轴对称图形的意义，判断轴对称图形的关键是寻找对称轴，看图形对折后两部分是否完全重合。

25．【分析】根据轴对称图形的意义：如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴；依次进行判断即可。

【解答】解：。

【点评】此题考查了轴对称图形的意义，判断轴对称图形的关键是寻找对称轴，看图形对折后两部分是否完全重合。

26．【分析】根据轴对称图形的意义：如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴，进行解答即可。

【解答】解：

【点评】此题考查了轴对称图形的意义，判断轴对称图形的关键是寻找对称轴，看图形对折后两部分是否完全重合。

六．解答题（共2小题）

27．【分析】把正方形纸沿虚线对角对折成为一个等腰直角三角形，再沿虚线对折，对折后仍为一个直角等腰三角形，然后直角边上裁剪一个小等腰直角三角形，展开后就是图2末的图形．

【解答】解：根据分析折叠、裁剪、展开如下图：

【点评】本题是考查单位图形的折叠问题，是锻炼学生动手操作能力．

28．【分析】此题需动手操作，仔细观察可知，剪去的部分位于各边长的正中间，是一个等腰三角形，据此作答．

【解答】解：仔细观察可知，剪去的部分位于各边长的正中间，是一个等腰三角形，故打开以后的形状是图2中上面的第2个图案，如图所示：

【点评】考查了简单图形的折叠问题，解答此题注意对折的方向以及对折的次数，可以实际操作一下，会变得简单明了．