专题10 截长补短模型综合应用（知识解读）-备战中考数学《重难点解读•专项训练》（全国通用）

这是一份专题10 截长补短模型综合应用（知识解读）-备战中考数学《重难点解读•专项训练》（全国通用），文件包含专题10截长补短模型综合应用知识解读-备战中考数学《重难点解读•专项训练》全国通用解析版docx、专题10截长补短模型综合应用知识解读-备战中考数学《重难点解读•专项训练》全国通用原卷版docx等2份试卷配套教学资源，其中试卷共33页， 欢迎下载使用。

专题10 截长补短模型综合应用（知识解读）
【专题说明】
“截长补短”是几何证明题中十分重要的方法，通常用来证明几条线段的数量关系，即若题目条件或结论中含有“a＋b＝c”的条件，需要添加辅助线时可以考虑“截长补短”的方法。
【方法技巧】
常见类型及常规解题思路：
① 可采取直接截长或补短，绕后进行证明。或者化为类型②证明。
② 可以将与构建在一个三角形中，然后证明这个三角形为特殊三角形，如等边三角形，等腰直角三角形，或一个角为的直角三角形等。

截长法常规辅助线：
（1）过某一点作长边的垂线
（2）在长边上截取一条与某一短边相同的线段，再证剩下的线段与另一短边相等。

补短法常规辅助线：
（1） 延长短边。
（2）通过旋转等方式使两短边拼合到一起

【典例分析】
【典例1】模型分析
当题目中出现线段的和差关系时，考虑用截长补短法，该类题日中常出现等腰三角形、角平分线等关键词句，采用截长补短法进行证明．
问题：
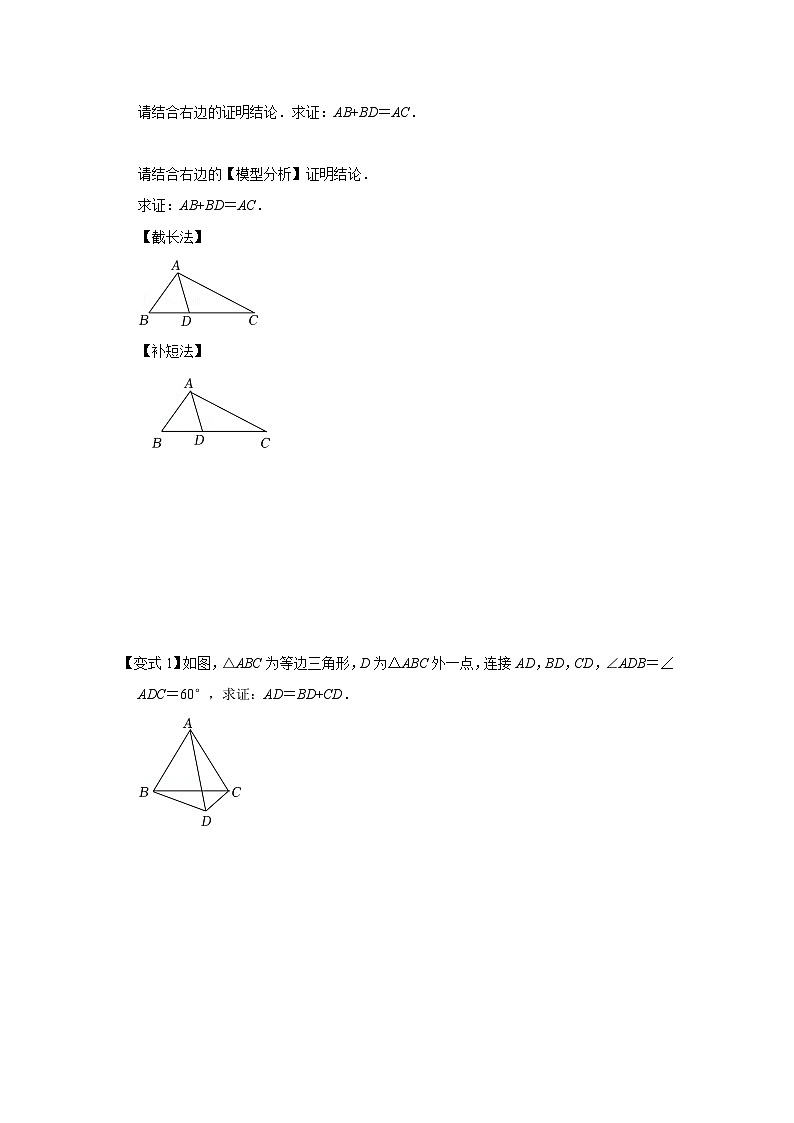
如图，在△ABC中，AD平分∠BAC交BC于点D，且∠B＝2∠C，求证：AB+BD＝AC．
截长法：
在AC上截取AE＝AB，连接DE，证明CE＝BD即可．

补短法：
延长AB至点F，使AF＝AC，连接DF，证明BF＝BD即可．
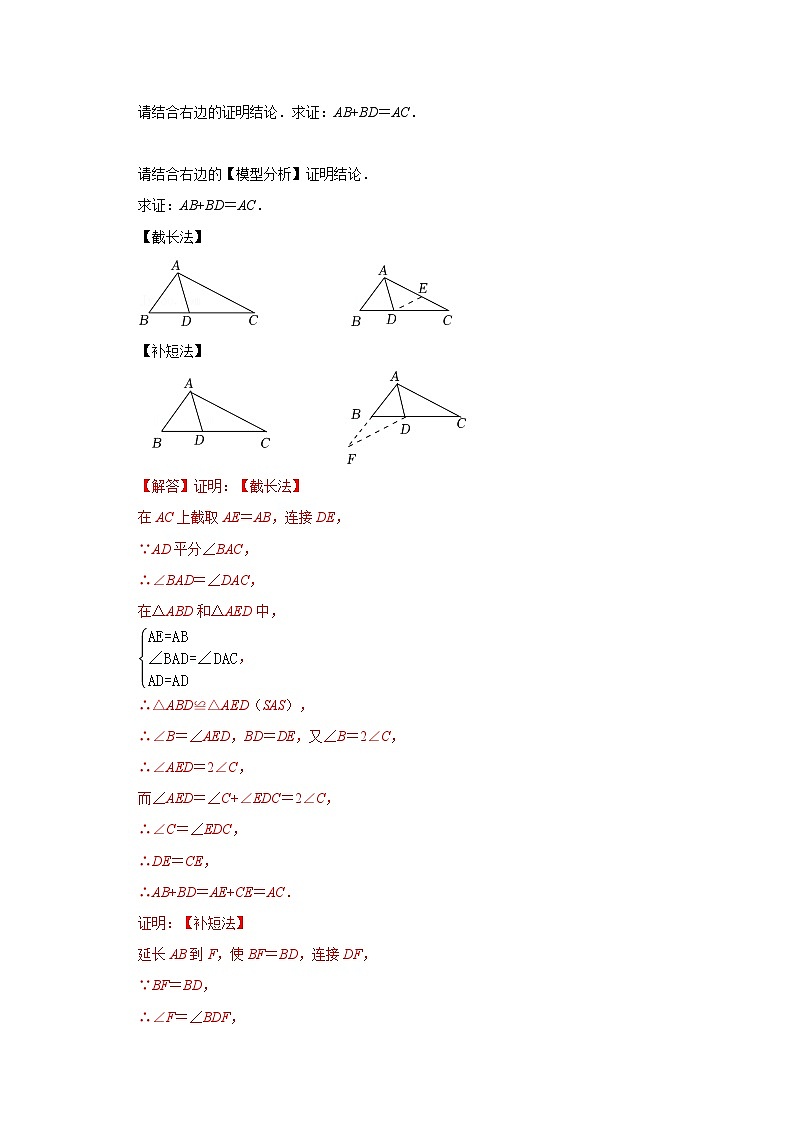
请结合右边的证明结论．求证：AB+BD＝AC．

请结合右边的【模型分析】证明结论．
求证：AB+BD＝AC．
【截长法】

【补短法】

【解答】证明：【截长法】
在AC上截取AE＝AB，连接DE，
∵AD平分∠BAC，
∴∠BAD＝∠DAC，
在△ABD和△AED中，
，
∴△ABD≌△AED（SAS），
∴∠B＝∠AED，BD＝DE，又∠B＝2∠C，
∴∠AED＝2∠C，
而∠AED＝∠C+∠EDC＝2∠C，
∴∠C＝∠EDC，
∴DE＝CE，
∴AB+BD＝AE+CE＝AC．
证明：【补短法】
延长AB到F，使BF＝BD，连接DF，
∵BF＝BD，
∴∠F＝∠BDF，
∴∠ABC＝∠F+∠BDF＝2∠F，且∠ABC＝2∠C，
∴∠C＝∠F，且∠CAD＝∠BAD，AD＝AD，
∴△ADF≌△ADC（AAS）
∴AC＝AF，
∴AC＝AF＝AB+BF＝AB+BD．
【变式1】如图，△ABC为等边三角形，D为△ABC外一点，连接AD，BD，CD，∠ADB＝∠ADC＝60°，求证：AD＝BD+CD．

【解答】证明：在DA上截取DE＝DB，连接BE，如下图所示，

∵∠ADB＝60°，DE＝DB，
∴△ABD为等边三角形，
∴∠EBD＝60°，BE＝BD，
∵△ABC为等边三角形，
∴∠ABC＝60°，BA＝BC，
∴∠EBD﹣∠EBC＝∠ABC﹣∠EBC，
∴∠ABE＝∠CBD，
在△ABE和△CBD中，
，
∴△ABE≌△CBD（SAS），
∴AE＝CD，
∴AD＝AE+ED＝CD+BD．
【变式2】如图，Rt△ABC中，AC＝BC，AD平分∠BAC交BC于点D，CE⊥AD交AD于F点，交AB于点E．求证：AD＝2DF+CE．

【解答】证明：在AF上截取FG＝DF，连接CG，则DG＝2DF，

∵∠ACB＝90°，
∴∠DCF+∠ACF＝90°，
又∵CF⊥AD，
∴∠ACF+∠CAF＝90°，
∴∠DCF＝∠CAF，
∵AD平分∠CAE，
∴∠CAF＝∠EAF，
∵DF＝FG，CF⊥DG，
∴CD＝CG，
∴∠CDG＝∠CGD，
∵∠DGC＝∠GAC+∠ACG，∠ADC＝∠B+∠BAD，
∴∠B＝∠ACG，
又∵AC＝BC，
∴△ACG≌△CBE（ASA），
∴AG＝CE，
∴AD＝AG+DG＝CE+2DF．
【变式3】如图，△ABC内接于⊙O，AC＝BC，CD是⊙O的一条弦，且＝，过点A作AP⊥CD，分别交CD，⊙O于点E，P，连接BP，若CD＝6，△ABP的周长为13，求AE的长．

【解答】解：在AE上截取AF＝BP，连接CF，PC，
∵AC＝BC，∠CAF＝∠CBP，
∴△CAF≌△CBP，
CF＝CP，
∵CD⊥PA，
∴EF＝PE，
∴AE＝AF+FE＝PB+PE，
∵AC＝BC，
∴＝，
∵＝，
∴＝，
∴AB＝CD＝6，
∵△ABP的周长是13，
∴AP+PB＝7，
∵AE＝PE+PB，
∴2AE＝AP+PB，
∴AE＝．
【变式4】如图，在△ABC中，AB＝AC，在AB左侧作∠BDC＝∠BAC＝α，过点A作AE⊥DC于点E．
（1）当α＝90°时，
①求证：AE＝DE；
②若BD＝AE＝2，请求出△ABC的面积；
（2）当α≠90°时，求证：BD+DE＝EC．

【解答】（1）①证明：过点B作BF⊥AE，交AE的延长线于点F，

∵AE⊥CD，
∴∠DEF＝90°，
又∵∠BDE＝90°，
∴四边形BDEF为矩形，
∴DE＝BF，
∵∠BAC＝90°，
∴∠BAF+∠EAC＝90°，
又∵∠EAC+∠ACE＝90°，
∴∠BAF＝∠ACE，
又∵∠AEC＝∠BFA＝90°，AB＝AC，
∴△ABF≌△CAE（AAS），
∴BF＝AE，
∴DE＝AE；
②解：∵四边形BDEF为矩形，BD＝AE＝2，
∴BD＝EF＝2，DE＝BF＝AE＝，
∴AF＝AE+EF＝+2，
∴BA2＝BF2+AF2＝＝8+4，
∴S△ABC＝＝；
（2）证明：过点A作AF⊥BD，交BD的延长线于F，连接AD，设CD与AB交于点O，

∵∠BDC＝∠BAC，∠BOD＝∠AOC，
∴∠ACO＝∠DOB，
即∠ABF＝∠ACE，
又∵∠AEC＝∠AFB＝90°，AC＝AB，
∴△ACE≌△ABF（AAS），
∴AE＝AF，BF＝CE，
又∵AD＝AD，
∴Rt△ADE≌Rt△ADF（HL），
∴DE＝DF，
∴CE＝BF＝BD+DF＝BD+DE．
【变式5】【问题背景】
如图①，在边长为1的正方形ABCD中，点E为射线BC上的一个动点（与点B，C不重合），连接AE，过点E作EF⊥AE，与正方形ABCD的外角∠DCG的平分线交于点F．李老师指出，当点E为线段BC的中点时，AE＝EF．
【初步探索】
（1）如图②，当点E在线段BC的延长线上时，其他条件不变，那么结论“AE＝EF”是否仍然成立；
【问题解决】
（2）当点E在线段BC上时，设BE＝x，△ECF的面积为y，求y与x之间的函数关系式；
【拓展延伸】
（3）如图③，将正方形ABCD放在平面直角坐标系xOy中，点O与点B重合，点C在x轴正半轴上，当点E运动到某一点时，点F恰好落在直线y＝﹣2x+3上，求此时点E的坐标．

【解答】解：【问题背景】
如图1，取AB的中点H，连接EH，

∵四边形ABCD是正方形，
∴AB＝BC，∠ABC＝90°＝∠BCD，
∵CF平分∠DCG，
∴∠DCF＝45°，
∴∠ECF＝135°，
∵E是BC的中点，
∴BH＝BE＝AH＝CE，
∴∠BHE＝∠BEH＝45°，
∴∠AHE＝∠ECF＝135°，
∵AE⊥EF，
∴∠AEB+∠FEC＝90°，
∵∠AEB+∠BAE＝90°，
∴∠FEC＝∠BAE，
∴△AHE≌△ECF（ASA），
∴AE＝EF；
【初步探索】
（1）仍然成立，理由如下：
如图2，在BA的延长线上取一点N，使AN＝CE，连接NE．

∵AB＝BC，AN＝CE，
∴BN＝BE，
∴∠N＝∠FCE＝45°，
∵四边形ABCD是正方形，
∴AD∥BE，
∴∠DAE＝∠BEA，
∴∠NAE＝∠CEF，
在△ANE和△ECF中，
，
∴△ANE≌△ECF（ASA），
∴AE＝EF；
【问题解决】
（2）如图3，在BA上截取BH＝BE，连接HE，
同理得：△AHE≌△ECF，

∴y＝S△AHE＝AH•BE＝x（1﹣x）＝﹣x2+x（0≤x≤1）；
【拓展延伸】
（3）如图4，在BA上截取BH＝BE，连接HE，过点F作FM⊥x轴于M，

设点E（a，0），
∴BE＝a＝BH，
∴HE＝a，
由（1）可得△AHE≌△ECF，
∴CF＝HE＝a，
∵CF平分∠DCM，
∴∠DCF＝∠FCM＝45°，
∵FM⊥CM，
∴∠CFM＝∠FCM＝45°，
∴CM＝FM＝a，
∴BM＝1+a，
∴点F（1+a，a），
∵点F恰好落在直线y＝﹣2x+3上，
∴a＝﹣2（1+a）+3，
∴a＝，
∴点E（，0）．
【典例2】如图1，在Rt△ABC中，AB＝BC，点D，E，F分别在AB，BC，AC边上，且DE＝EF，∠DEF＝∠B，∠A＝45°．
（1）试猜想CF与BE之间的数量关系，并证明；
（2）自主探究：如图2，若将已知条件中含45°的直角三角形换成含30°的直角三角形，其余条件不变，试探究BE和CF的关系．

【解答】解：（1）CF与BE之间的数量关系为：CF＝BE．理由：
过点F作FH⊥BC于点H，如图，

∵Rt△ABC中，AB＝BC，∠A＝45°，
∴∠C＝45°，∠B＝90°．
∵∠DEF＝∠B，
∴∠DEF＝90°，
∴∠DEB+∠FEH＝90°．
∵∠BDE+∠DEB＝90°，
∴∠BDE＝∠FEH．
在△BDE和△HEF中，
，
∴△BDE≌△HEF（AAS），
∴BE＝FH．
∵FH⊥BC，∠C＝45°，
∴△FHC为等腰直角三角形，
∴FC＝FH，
∴FC＝BE；
（2）CF与BE之间的数量关系为：CF＝BE．理由：
过点F作FH⊥BC于点H，如图，

∵Rt△ABC中，∠A＝30°，
∴∠C＝60°，∠B＝90°．
∵∠DEF＝∠B，
∴∠DEF＝90°，
∴∠DEB+∠FEH＝90°．
∵∠BDE+∠DEB＝90°，
∴∠BDE＝∠FEH．
在△BDE和△HEF中，
，
∴△BDE≌△HEF（AAS），
∴BE＝FH．
∵FH⊥BC，∠C＝60°，
∴sin60°＝，
∴FC＝FH，
∴FC＝BE．
【变式1】如图，在△ABC中，∠ABC＝45°，AD⊥BC于点D，点F是AC上一点，连接BF交AD于点E，且DE＝CD，连接DF，若AF＝4，DF＝2，则BF的长为 　 　．

【解答】解：如图，在BF上截取HF＝AF，连接AH，

∵∠ABC＝45°，AD⊥BC，
∴AD＝BD，∠ADB＝∠ADC＝90°，
在△BDE和△ADC中，
，
∴△BDE≌△ADC（SAS），
∴∠EBD＝∠CAD，
∵∠BED＝∠AEF，
∴∠AFE＝∠BDE＝90°，
∴∠AHF＝∠HAF＝45°，
∴AH＝AF，
∴∠BAH＝∠DAF，∠AHB＝135°，
∠AEF＝∠BED，∠AFE＝∠BDE＝90°，
∴△AFE∽△BDE，
∴＝，
∵∠AEB＝∠FED，
∴△AEB∽△FED，
∴∠EAB＝∠EFD＝45°，
∴∠AFD＝∠AFH+∠EFD＝90°+45°＝135°，
∴∠AHB＝∠AFD，
∴△AHB∽△AFD，
∴＝＝，
∴BH＝DF，
∴BF＝BH+HF＝DF+AF＝2+4．
故答案为：2+4．
【变式2】如图，四边形ABCD内接于⊙O，BC是⊙O的直径，连接AC，BD，若AB＝AC，请探究AD，BD，DC之间的数量关系．

【解答】解：作AE⊥AD交BD于E，
∵BC是直径，
∴∠BAC＝90°，
∵∠BAE+∠EAC＝∠DAC+∠EAC＝90°，
∴∠BAE＝∠CAD，
∵∠ABD＝∠ACD，AB＝AC，
∴△ABE≌△ACD（SAS），
∴BE＝CD，
∵△AED是等腰直角三角形，
∴DE＝AD，
∵BD＝DE+BE，
∴BD＝AD+CD．

【变式3】如图，在△ABC中，∠ACB＝120°，BC＞AC，点E在BC上，点D在AB上，CE＝CA，连接DE，∠ACB+∠ADE＝180°，CH⊥AB，垂足为点H．求证：DE+AD＝2CH．

【解答】证明：如图，作∠FCD＝∠ACB，交BA延长线于F，

∵∠FCA+∠ACD＝∠ACD+∠DCB，
∴∠FCA＝∠DCB，
∵∠ACB＝120°，∠ACB+∠ADE＝180°，
∴∠EDB＝120°，∠EDA＝60°，
∵∠FAC＝120°+∠B，∠CED＝120°+∠B，
∴∠FAC＝∠CED，
在△AFC和△EDC中，
，
∴△AFC≌△EDC（ASA），
∴AF＝DE，FC＝CD，
∵CH⊥FD，
∴FH＝HD，∠FCH＝∠HCD＝60°，
∴DH＝CH，
∵AD+DE＝AD+AF＝FD＝2DH＝2CH，
∴AD+DE＝2CH．
【变式4】如图，在△ABC中，AB＝AC，∠BAC＝90°，点D是平面内一点，且AD⊥CD．点O是BC的中点，连接OA，OD．
（1）如图①，若点D是BC下方一点，过点O作OE⊥OD分别交AC，AD于点E，F．
①求证：∠OAF＝∠OCD；
②若CD＝1，DF＝2，求BC的长；
（2）如图②，若点D是AC右侧一点，试判断AD，CD，OD之间的数量关系，并说明理由．

【解答】（1）①证明：∵AB＝AC，O为BC的中点，
∴OA＝OB＝OC，OA⊥OC，
∵OE⊥OD，
∴∠AOC＝∠EOD＝90°，
∴∠AOF＝∠COD，
∵∠AOM＝∠MDC＝90°，∠AMO＝∠CMD，
∴∠OAM＝∠MCD，
∴△OAF≌△OCD（ASA），
∴∠OAF＝∠OCD；
②解：∵△OAF≌△OCD，
∴AF＝CD＝1，
∵DF＝2，
∴AD＝AF+DF＝1+2＝3，
∵AD⊥DC，
∴∠ADC＝90°，
∴AC＝＝＝，
∵AC＝AB，
∴BC＝AC＝＝2；
（2）解：AD+CD＝OD．
理由：过点O作OE⊥OD，交DA的延长线于点E，

∵∠DOE＝∠AOC＝90°，
∴∠AOE＝∠COD，
∵∠ODC+∠+ODA＝90°，∠ODA+∠OEA＝90°，
∴∠ODC＝∠OEA，
又∵OA＝OC，
∴△OCD≌△OAE（AAS），
∴CD＝AE，OD＝OE，
∴DE＝OD，
∴AD+AE＝AD+CD＝OD．
【变式5】【问题探究】
如图，△ABC是等腰三角形，AB＝AC，点D是平面内一点，连接AD，BD，CD，且∠CAB＝∠CDB．
（1）如图①，当∠CAB＝60°时，试探究BD，CD，AD之间的数量关系；
（2）如图②，当∠CAB＝120°时，探究是否为定值，并说明理由；
【问题解决】
（3）如图③，在四边形ADBC中，AB＝AC，∠CAB＝∠CDB＝120°，若AD＝2，BD＝3，求CD的长．

【解答】解：（1）BD，CD，AD之间的数量关系为：BD＝CD+AD，理由如下：
在BD上取一点E，使BE＝CD，连接AE，设AC交BD于H，如图①所示：
∵∠CAB＝∠CDB，∠AHB＝∠CHD，
∴∠ABE＝∠ACD，
在△ABE和△ACD中，
，
∴△ABE≌△ACD（SAS），
∴AD＝AE，∠DAC＝∠EAB，
∴∠DAC+∠CAE＝∠EAB+∠CAE＝∠CAB＝60°，
∴△ADE是等边三角形，
∴DE＝AD，
∴BD＝BE+DE＝CD+AD；
（2）是定值，理由如下：
在BD上取一点E，使BE＝CD，连接AE，设AC交BD于H，过点A作AF⊥BD于F，如图②所示：
∵∠CAB＝∠CDB，∠AHB＝∠CHD，
∴∠ABE＝∠ACD，
在△ABE和△ACD中，
，
∴△ABE≌△ACD（SAS），
∴AD＝AE，∠DAC＝∠EAB，
∴∠DAC+∠CAE＝∠EAB+∠CAE＝∠CAB＝120°，
∴∠ADE＝∠AED＝（180°﹣120°）＝30°，
∵AF⊥DE，
∴DF＝EF，AF＝AD，
在Rt△AFD中，由勾股定理得：DF＝＝＝AD，
∴DE＝2DF＝AD，
∵DE＝BD﹣BE＝BD﹣CD，
∴BD﹣CD＝AD，
∴＝，
∴是定值；
（3）在CD上取一点E，使CE＝BD，连接AE，设AB交CD于H，过点A作AF⊥CD于F，如图③所示：
∵∠CAB＝∠CDB，∠AHC＝∠BHD，
∴∠ACE＝∠ABD，
在△ACE和△ABD中，
，
∴△ACE≌△ABD（SAS），
∴AE＝AD，∠EAC＝∠DAB，
∴∠EAC+∠BAE＝∠DAB+∠BAE＝∠CAB＝120°，
∴∠ADE＝∠AED＝（180°﹣120°）＝30°，
∵AF⊥DE，
∴DF＝EF，AF＝AD，
在Rt△AFD中，由勾股定理得：DF＝＝＝AD，
∴DE＝2DF＝AD，
∴CD＝CE+DE＝BD+AD＝3+×2＝3+2．



【变式6】如图，在矩形ABCD中，AB＝AD，点E为CD延长线上一点，连接AE，过点C作CF⊥AE于点F，CF交AD于点H，过点D作DN⊥AE于点N，连接DF．
（1）在不添加辅助线的情况下，找出一个与△CDH相似的三角形，并证明；
（2）求证：FD＝2DN；
（3）求证：CF＝AF+2FD．

【解答】（1）解：选择△AFH，
证明：∵四边形ABCD是矩形，
∴∠ADC＝90°，
∵CF⊥AE，
∴∠AFC＝90°，
∴∠AFH＝∠CDH，
∵∠AHF＝∠CHD，
∴△AFH∽△CDH；
（2）证明：连接AC，

∵△AFH∽△CDH，
∴，
∴，
∵∠FHD＝∠AHC，
∴△FHD∽△AHC，
∴∠DFC＝∠DAC，
∵AB＝CD＝AD，
∴∠DAC＝60°，
∴∠DFC＝∠DAC＝60°，
∴∠DFN＝30°，
∵DN⊥AE，
∴∠DNF＝90°，
∴FD＝2DN；
（3）证明：在线段FC上截取FO，使FO＝AF，连接AO，

∵∠AFO＝90°，
∴FAO＝60°，
∵∠DAC＝60°，
∴∠FAD＝∠OAC，
∵，
∴△FAD∽△OAC，
∴，
∴OC＝2FD，
∴CF＝FO+OC＝AF+2FD，
∴CF＝AF+2FD．