专题01 角平分线四大模型在三角形中的应用（能力提升）-备战中考数学《重难点解读•专项训练》（全国通用）

专题01  角平分线四大模型在三角形中的应用（能力提升）

1．如图：在四边形ABCD中，BC＞DA，AD＝DC，BD平分∠ABC，DH⊥BC于H，求证：

（1）∠DAB+∠C＝180°

（2）BH＝（AB+BC）

2．如图，AD∥BC，∠D＝90°，∠CPB＝30°，∠DAB的角平分线与∠CBA的角平分线相交于点P，且D，P，C在同一条直线上．

（1）求∠PAD的度数；

（2）求证：P是线段CD的中点．

3．如图，梯形ABCD中，AD∥BC，E是CD的中点，AE平分∠BAD，AE⊥BE．

（1）求证：BE平分∠ABC；

（2）求证：AD+BC＝AB；

（3）若S△ABE＝4，求梯形ABCD的面积．

4．【问题提出】在△ABC中，∠ACB＝2∠B，AD为∠BAC的角平分线，探究线段AB，AC，CD的数量关系．

【问题解决】如图1，当∠ACB＝90°，过点D作DE⊥AB，垂足为E，易得AB＝AC+CD；由此，如图2，当∠ACB≠90°时，猜想线段AB，AC，CD有怎样的数量关系？给出证明．

【方法迁移】如图3，当∠ACB≠90°，AD为△ABC的外角平分线时，探究线段AB，AC，CD又有怎样的数量关系？直接写出结论，不证明．

5．已知：如图，在Rt△ABC中，∠A＝90°，AB＝AC，点D在BC上，点E与点A在BC的同侧，且∠CED＝90°，∠B＝2∠EDC．

（1）求证：∠FDC＝∠ECF；

（2）若CE＝1，求DF的长．

6．如图，已知在△ABC中，∠BAC＝90°，AB＝AC，BD平分∠ABC，CE⊥BD交BD的延长线于点E．

求证：CE＝BD．

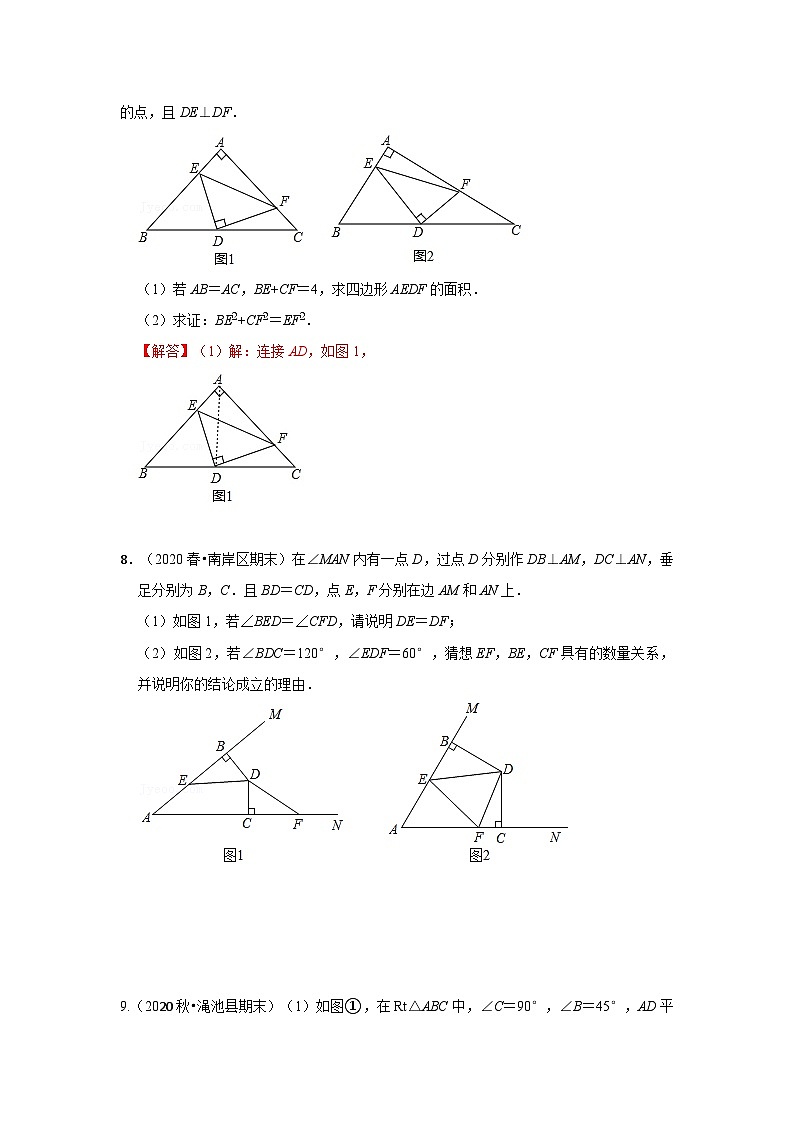
7．如图，在△ABC中，∠CAB＝90°，D是斜边BC上的中点，E、F分别是AB、AC边上的点，且DE⊥DF．

（1）若AB＝AC，BE+CF＝4，求四边形AEDF的面积．

（2）求证：BE2+CF2＝EF2．

【解答】（1）解：连接AD，如图1，

8．（2020春•南岸区期末）在∠MAN内有一点D，过点D分别作DB⊥AM，DC⊥AN，垂足分别为B，C．且BD＝CD，点E，F分别在边AM和AN上．

（1）如图1，若∠BED＝∠CFD，请说明DE＝DF；

（2）如图2，若∠BDC＝120°，∠EDF＝60°，猜想EF，BE，CF具有的数量关系，并说明你的结论成立的理由．

9.（2020秋•渑池县期末）（1）如图①，在Rt△ABC中，∠C＝90°，∠B＝45°，AD平分∠BAC，交BC于点D．如果作辅助线DE⊥AB于点E，则可以得到AC、CD、AB三条线段之间的数量关系为　       ；

（2）如图，△ABC中，∠C＝2∠B，AD平分∠BAC，交BC于点D．（1）中的结论是否仍然成立？若不成立，试说明理由；若成立，请证明．

10.（百色期末）如图，△ABC中，AD平分∠BAC，DG⊥BC且平分BC，DE⊥AB于E，DF⊥AC于F．

（1）说明BE＝CF的理由；

（2）如果AB＝5，AC＝3，求AE、BE的长．

11.（广州期中）如图，在△ABC中，∠ABC的平分线与∠ACB的外角的平分线相交于点D．

（1）求证：点D到三边AB、BC、CA所在直线的距离相等；

（2）连接AD，若∠BDC＝40°，求∠DAC的度数．

12．（2021秋•雨花区期末）如图，△ABC中，∠ABC＝60°，AD、CE分别平分∠BAC、∠ACB，AD、CE相交于点P．

（1）求∠APC的度数；

（2）若AE＝3，CD＝4，求线段AC的长．

13．（2020秋•南开区校级期中）如图1，在平面直角坐标系中，直线AB分别交x轴、y轴于A（a，0）、B（0，b）两点，且a，b满足（a﹣b）2+|a﹣4t|＝0，且t＞0，t是常数．直线BD平分∠OBA，交x轴于D点．

（1）若AB的中点为M，连接OM交BD于N，求证：ON＝OD；

（2）如图2，过点A作AE⊥BD，垂足为E，猜想AE与BD间的数量关系，并证明你的猜想；

（3）如图3，在x轴上有一个动点P（在A点的右侧），连接PB，并作等腰Rt△BPF，其中∠BPF＝90°，连接FA并延长交y轴于G点，当P点在运动时，OG的长是否发生改变？若改变，请求出它的变化范围；若不变，求出它的长度．