华师大版七年级下册第9章 多边形9.2 多边形的内角和与外角和课时作业

这是一份华师大版七年级下册第9章 多边形9.2 多边形的内角和与外角和课时作业，共11页。
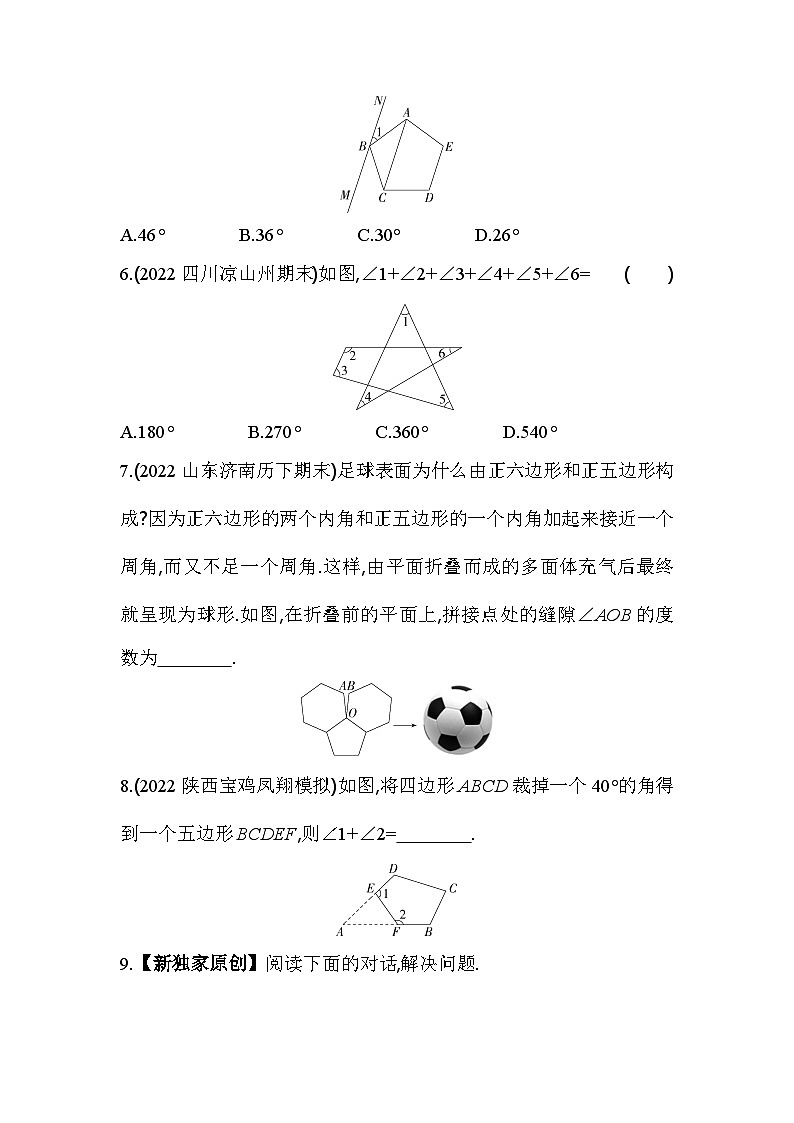
9.2　多边形的内角和与外角和基础过关全练知识点1　多边形的有关概念1.下列选项中的图形,不是凸多边形的是 (　　)2.(2022山东淄博沂期中)已知过一个多边形的某一个顶点共可作2 022条对角线,则这个多边形的边数是 (　　)A.2 022　　　　B.2 023　　　　C.2 024　　　　D.2 025知识点2　多边形的内角和3.【主题教育·生命安全与健康】(2022山东临沂中考)下图是某一水塘边的警示牌,牌面是五边形,这个五边形的内角和是              (　　)A.900°　　　　B.720°　　　　C.540°　　　　D.360°4.(2022湖南怀化中考)一个多边形的内角和为900°,则这个多边形是              (　　)A.七边形　　　　B.八边形　　　　C.九边形　　　　D.十边形5.(2022山西模拟)如图,直线MN经过正五边形ABCDE的顶点B,连结AC,若MN∥AC,则∠1的度数为              (　　)A.46°　　　　B.36°　　　　C.30°　　　　D.26°6.(2022四川凉山州期末)如图,∠1+∠2+∠3+∠4+∠5+∠6= (　　)A.180°　　　　B.270°　　　　C.360°　　　　D.540°7.(2022山东济南历下期末)足球表面为什么由正六边形和正五边形构成?因为正六边形的两个内角和正五边形的一个内角加起来接近一个周角,而又不足一个周角.这样,由平面折叠而成的多面体充气后最终就呈现为球形.如图,在折叠前的平面上,拼接点处的缝隙∠AOB的度数为　　　　. 8.(2022陕西宝鸡凤翔模拟)如图,将四边形ABCD裁掉一个40°的角得到一个五边形BCDEF,则∠1+∠2=　　　　. 9.【新独家原创】阅读下面的对话,解决问题.(1)小明计算的是几边形的内角和?少算的那个内角的度数是多少?(2)请正确计算这个多边形的内角和.    知识点3　多边形的外角和10.(2022广东东莞一模)如图,在六边形ABCDEF中,若∠1+∠2+∠3=140°,则∠4+∠5+∠6=              (　　)A.200°　　　　B.40°　　　　C.160°　　　　D.220°11.(2022北京朝阳一模)下列多边形中,内角和与外角和相等的是 (　　)  A   B  C   D12.(2022河北邯郸模拟)求下列多边形的边数.(1)若一个正n边形的每一个外角都等于60°,则n=　　　　; (2)若一个n边形的内角和是外角和的3倍,则n=　　　　. 能力提升全练13.(2022河北中考,5,)如图,将三角形纸片剪掉一角得到四边形,设△ABC与四边形BCDE的外角和的度数分别为α,β,则正确的是(　　)A.α-β=0B.α-β<0C.α-β>0D.无法比较α与β的大小14.【教材变式·P88习题T2变式】(2022江苏无锡锡山天一实验学校月考,7,)如图,∠F=90°,∠A+∠B+∠C+∠D+∠E的度数为              (　　)A.90°　　  　　B.180°　　　　C.270°　　　　D.360°15.(2022湖南株洲中考,17,)如图所示,已知∠MON=60°,正五边形ABCDE的顶点A、B在射线OM上,顶点E在射线ON上,则∠AEO=　　　　度. 16.(2022江苏无锡锡山期中,16,)如图,在四边形ABCD中,∠DAB的平分线与∠CBE的平分线相交于点P,且∠D+∠C=260°,则∠P=　　　　°. 17.【学科素养·推理能力】(2021福建泉州永春月考,22,)如图,已知六边形ABCDEF的每个内角都相等,连结AD.(1)若∠1=48°,求∠2的度数;(2)求证:AB∥DE.         素养探究全练18.【推理能力】(2021江苏南京郑和外国语学校期中)如图1,我们分别研究过三角形中两内角平分线所成的∠BIC、两外角平分线所成的∠BDC、一内角一外角平分线所成的∠BEC与∠A的关系.(1)如图2,在四边形ABCD中,BP、CP分别平分∠ABC和∠BCD,则∠P与∠A、∠D的数量关系为　　　　　　　　; (2)如图3,BM、CM分别平分∠EBC和∠BCF,请探究∠M与∠A、∠D的数量关系,并说明理由;(3)如图4,BF为∠ABC的平分线,CF为∠DCE的平分线,若设∠A=α,∠D=β,则∠F=　　　　.(用含α、β的式子表示)                 图1                                 图2                                     图3                                      图4
答案全解全析基础过关全练1.A　根据凸多边形的定义知,不是凸多边形的是选项A中的图形.2.D　设多边形为n边形,则n-3=2 022,解得n=2 025.故选D.3.C　(5-2)×180°=540°,故选C.4.A　设多边形的边数为n,则(n-2)·180°=900°,解得n=7.故这个多边形是七边形.故选A.5.B　由题意得∠ABC==108°,∵BC=BA,∴∠BAC=∠BCA==36°,∵MN∥AC,∴∠1=∠BAC=36°.故选B.6.C　如图所示,∵∠4+∠6=∠7,∠1+∠5=∠8,∠3+∠2+∠7+∠8=360°,∴∠1+∠2+∠3+∠4+∠5+∠6=360°,故选C.7.答案   12°解析　正五边形的每个内角的度数为×(5-2)×180°=108°,正六边形的每个内角的度数为×(6-2)×180°=120°,∴∠AOB的度数为360°-108°-120°×2=12°.故答案为12°.8. 答案   220°解析　在△AEF中,∠AEF+∠AFE=180°-∠A=140°,∴∠1+∠2=360°-140°=220°,故答案为220°.9.解析　(1)设这个多边形的边数为n,根据题意得2 022°<(n-2)×180°<2 022°+180°,解得13,所以n=14,小明算的是十四边形的内角和.根据多边形的内角和可得(14-2)×180°-2 022°=138°,所以小明少算的那个内角的度数为138°.(2)十四边形的内角和为(14-2)×180°=2 160°.10.D　∵∠1+∠2+∠3+∠4+∠5+∠6=360°,∠1+∠2+∠3=140°,∴∠4+∠5+∠6=360°-140°=220°,故选D.11.B　设所求多边形的边数为n,根据题意得(n-2)·180°=360°,解得n=4.故选B.12. 答案   (1)6　(2)8解析　(1)∵n边形的外角和等于360°,一个正n边形的每一个外角都等于60°,∴n==6,故答案为6.(2)∵一个n边形的内角和是外角和的3倍,∴(n-2)·180°=360°×3,解得n=8,故答案为8.能力提升全练13.A　∵任意多边形的外角和为360°,∴α=β=360°,∴α-β=0.故选A.14.C　如图,连结BE,易得∠C+∠D=∠1+∠2,∵四边形ABEF中,∠A+∠ABE+∠BEF+∠F=360°,∴∠A+∠ABC+∠1+∠2+∠DEF+∠F=360°,∴∠A+∠ABC+∠C+∠D+∠DEF+∠F=360°,∵∠F=90°,∴∠A+∠ABC+∠C+∠D+∠DEF=270°,故选C.15. 答案   48解析　∵五边形ABCDE是正五边形,∴∠EAB==108°,∵∠EAB是△AEO的外角,∴∠AEO=∠EAB-∠MON=108°-60°=48°,故答案为48.16. 答案   40解析　∵∠D+∠C=260°,∠DAB+∠ABC+∠C+∠D=360°,∴∠DAB+∠ABC=100°,又∵∠DAB的平分线与∠CBE的平分线相交于点P,∴∠PAB+∠ABP=(180°-∠ABC)=90°+(∠DAB+∠ABC)=90°+×100°=140°,∴∠P=180°-(∠PAB+∠ABP)=40°.故答案为40.17.解析　(1)∵六边形ABCDEF的每个内角都相等,∴每一个内角的大小为=120°,∴∠E=∠F=∠BAF=120°.又∵∠1=48°,∴∠FAD=∠FAB-∠DAB=120°-48°=72°.∵∠2+∠FAD+∠F+∠E=360°,∴∠2=360°-∠FAD-∠F-∠E=360°-72°-120°-120°=48°.(2)证明:∵∠1=120°-∠DAF,∠2=360°-120°-120°-∠DAF=120°-∠DAF,∴∠1=∠2,∴AB∥DE.素养探究全练18.解析　(1)∠P=(∠A+∠D).提示:由三角形的内角和得,∠P=180°-(∠PBC+∠PCB),由四边形的内角和得,∠ABC+∠DCB=360°-(∠A+∠D),∵BP、CP分别平分∠ABC和∠BCD,∴∠PBC+∠PCB=(∠ABC+∠DCB),∴∠P=180°-[360°-(∠A+∠D)]=(∠A+∠D).(2)∠M=180°-(∠A+∠D).理由:∵∠EBC=180°-∠ABC,∠FCB=180°-∠DCB,BM平分∠EBC,CM平分∠FCB,∴∠MBC=∠ABC,∠MCB=∠DCB,∴∠MBC+∠MCB=180°-(∠ABC+∠DCB),∵四边形ABCD中,∠ABC+∠DCB=360°-(∠A+∠D),△MBC中,∠M=180°-(∠MBC+∠MCB)=(∠ABC+∠DCB),∴∠M=×[360°-(∠A+∠D)]=180°-(∠A+∠D).(3)∠F=(α+β)-90°.提示:由三角形外角的性质可得,∠F=∠FCE-∠FBC,∵BF平分∠ABC,CF平分∠DCE,∴∠F=(∠DCE-∠ABC)=(180°-∠DCB-∠ABC)=90°-(∠DCB+∠ABC),∵∠DCB+∠ABC=360°-(α+β),∴∠F=90°-[360°-(α+β)]=(α+β)-90°.