海南省海口市2023届高三第二次模拟考试数学试卷（含解析）

海南省海口市2023届高三第二次模拟考试数学试卷

学校:___________姓名：___________班级：___________

一、单选题

1．已知集合，，则

A． B．

C． D．

2．已知复数，则的虚部是（    ）

A． B． C． D．

3．设集合、是全集的两个子集，则“”是“”的（    ）

A．充分不必要条件 B．必要不充分条件

C．充要条件 D．既不充分也不必要条件

4．某辆汽车每次加油都把油箱加满，下表记录了该车相邻两次加油时的情况．（注：“累计里程”指汽车从出厂开始累计行驶的路程）在这段时间内，该车每100千米平均耗油量为（    ）

A．6升 B．8升 C．10升 D．12升

5．已知为等差数列，，，则等于（    ）

A．-1 B．1 C．3 D．7

6．已知双曲线（，）的渐近线与圆有交点，则的离心率的取值范围是

A． B． C． D．

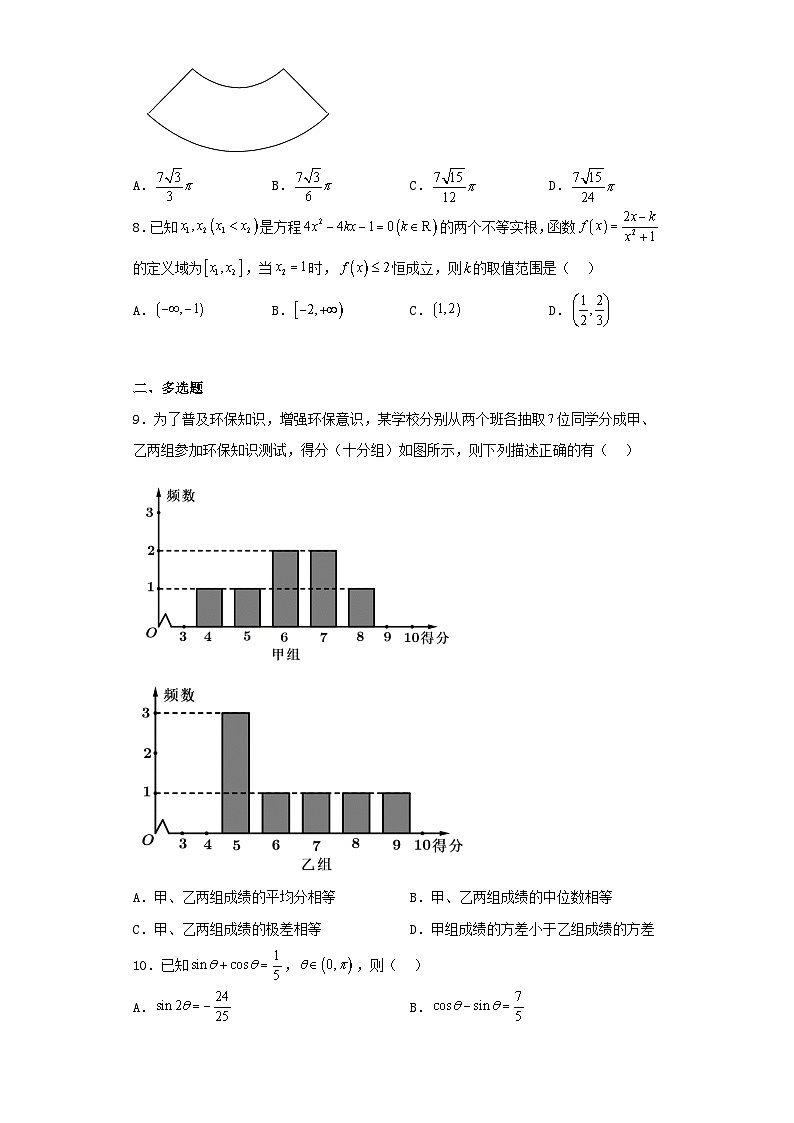
7．如图是一个圆台的侧面展开图，其面积为，两个圆弧所在的圆半径分别为2和4，则该圆台的体积为（    ）

A． B． C． D．

8．已知是方程的两个不等实根，函数的定义域为，当时，恒成立，则的取值范围是（    ）

A． B． C． D．

二、多选题

9．为了普及环保知识，增强环保意识，某学校分别从两个班各抽取位同学分成甲、乙两组参加环保知识测试，得分（十分组）如图所示，则下列描述正确的有（    ）

A．甲、乙两组成绩的平均分相等 B．甲、乙两组成绩的中位数相等

C．甲、乙两组成绩的极差相等 D．甲组成绩的方差小于乙组成绩的方差

10．已知，，则（    ）

A． B．

C． D．

11．（多选）如图已知正方体的棱长为a，点E，F，G分别为棱的中点，下列结论中正确的是（    ）

A．平面 B．平面

C．异面直线与所成角的正切值为 D．四面体的体积等于

12．关于函数，下列结论正确的有（    ）

A．在上是增函数

B．存在唯一极小值点

C．在上有一个零点

D．在上有两个零点

三、填空题

13．函数 的最小正周期为__________．

14．已知向量，且，则__________．

15．为增强学生的劳动意识，某校组织两个班级的学生参加社区劳动，这两个班级拟从高一年段的两个班级和高二年段的四个班级中选出，则选出的班级中至少有一个班级来自高一年段的概率为______________.

16．若直线与抛物线交于两点，若线段的中点的横坐标是3，则______________

四、解答题

17．如图，已知△ABC的内角A，B，C所对的边分别是a，b，c，．

(1)求角C：

(2)若，，延长CB至M，使得，求BM．

18．已知数列的前项和为，且，数列中，.

（1）求的通项公式；

（2）若，，求数列的前项和.

19．已知三棱柱中，.

(1)求证: 平面平面.

(2)若，在线段上是否存在一点使平面和平面所成角的余弦值为 若存在，确定点的位置；若不存在，说明理由.

20．某P2P平台需要了解该平台投资者的大致年龄分布，发现其投资者年龄大多集中在区间岁之间，对区间岁的人群随机抽取20人进行了一次理财习惯调查，得到如下统计表和各年龄段人数频率分布直方图：

（1）求a的值并画出频率分布直方图；

（2）从被调查的20人且年龄在岁中的投资者中随机抽取3人调查对其P2P理财观念的看法活动，记这3人中来自区间岁年龄段的人数为X，求随机变量X的分布列及数学期望.

21．已知椭圆：的一个焦点为. 经过点的直线与椭圆交于，两点.

(1)求椭圆方程；

(2)当直线的倾斜角为时，求线段的长．

22．已知函数，，.

（1）求的最大值；

（2）若对，总存在使得成立，求的取值范围；

（3）证明不等式：.

参考答案：

1．A

【详解】试题分析：由题意得，，则，所以，故选A.

考点：集合的运算．

2．B

【分析】根据复数的除法法则求复数z的代数形式，再得到其共扼复数的虚部．

【详解】复数，则，的虚部为．

故选：B.

3．C

【解析】作出韦恩图，数形结合，即可得出结论.

【详解】如图所示，，

同时.

故选:C.

【点睛】本题考查集合关系及充要条件，注意数形结合方法的应用，属于基础题.

4．B

【分析】求出这段时间的行驶里程和耗油量即可计算.

【详解】由题意知，该车行驶千米，耗油48升，

所以在这段时间内，该车每100千米平均耗油量为升.

故选：B.

5．B

【分析】利用等差数列的通项公式，列出方程组，求出首项和公差，由此能求出．

【详解】为等差数列，，，

，，

，，，

，

．

故选：.

【点睛】本题考查等差数列项的求法，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．

6．A

【分析】本道题结合双曲线方程，得到渐近线方程，利用圆与渐近线有交点，得出圆心到渐近线的距离小于等于半径，利用点到直线距离公式，建立不等式，计算离心率范围，即可．

【详解】结合双曲线方程可知渐近线方程为，将圆方程转化为标准方程得到，得到圆心O的坐标为，要使得圆与渐近线方程有交点，关键使得圆心O到渐近线距离小于等于半径，结合点到直线距离，建立不等式，得到

，解得，利用，代入，得到，解得

，故选A．

【点睛】本道题考查了点到直线距离公式以及直线与圆位置关系，考查了双曲线的性质，关键抓住交点，建立不等式，即可，属于中档题．

7．D

【分析】由条件结合扇形面积公式可求圆台的上下底面的半径，结合圆台的轴截面图形可求圆台的高，利用圆台体积公式求其体积.

【详解】圆台的侧面展开图是一扇环，设该扇环的圆心角为，

则其面积为，得，

所以扇环的两个圆弧长分别为和，

设圆台的上底半径，下底半径分别为，圆台的高为，

则

所以，，又圆台的母线长

所以圆台的高为，

所以圆台的体积为．

故选：D.

8．B

【分析】对函数求导数，根据是方程的两个不等实根，得出恒成立，进而有，即可求解

【详解】

，

因为是方程的两个不等实根，

显然时，，

所以，

所以，恒成立，

所以在单调递增，

所以，

又当时，恒成立，

所以，即，解得，

故选：B

9．BCD

【解析】根据条形统计图计算出甲、乙两组成绩的平均分、中位数、极差与方差，进而可判断各选项的正误.

【详解】对于A选项，甲组成绩的平均数为，

乙组成绩的平均分为，

所以甲组成绩的平均分小于乙组成绩的平均分，A选项错误；

对于B选项，甲、乙两组成绩的中位数都为，B选项正确；

对于C选项，甲、乙两组成绩的极差都为，C选项正确；

对于D选项，甲组成绩的方差为，

乙组成绩的方差为，

所以甲组成绩的方差小于乙组成绩的方差，D选项正确.

故选：BCD.

10．AC

【分析】多项选择题，需要对选项一一验证：

借助于先求出，可以直接求出的值，判断B;

用判断C，二倍角公式判断A、D选项；

【详解】∵，，且

解得：

∴，故A正确；

，故B错误；

，故C正确；

∵，∴.

∵，∴，故D错误.

故选：AC

【点睛】利用三角公式求三角函数值的关键：

(1)角的范围的判断；

(2)对于三角函数求值题，一般是先化简，再求值．

11．BC

【分析】对于选项,通过作辅助线证明与平面相交，故A不正确；

对于选项,证明，，所以平面即得证，故B正确；

对于选项,利用向量法求出异面直线与所成角的正切值为，故C正确；

对于选项,四面体的体积等于,故D不正确.

【详解】如图所示，取的中点H，的中点I，的中点M，连接并延长，连接并延长，记与的延长线交于点P，延长，记的反向延长线交的反向延长线于点Q，的延长线交的反向延长线于点N.连接，

因为与相交，故与平面相交，故A不正确.

∵，平面,

∴平面，

∴.

∵，平面，

∴平面，

∴，

又，平面，

∴平面，故B正确.

以D为原点，所在直线分别为x轴，y轴，z轴，建立空间直角坐标系，

则，

∴，

∴

，

∴，

∴，

∴异面直线与所成角的正切值为，故C正确.

易知四面体的体积等于正方体的体积减去四个正三棱锥的体积，

即，故D不正确.

故选：BC.

【点睛】本题主要考查空间直线平面位置关系的判断和证明，考查空间角的计算，考查几何体体积的计算，意在考查学生对这些知识的理解掌握水平和分析推理计算能力.

12．ABD

【解析】根据函数求得与，再根据在恒成立，确定在上单调递增，及，且存在唯一实数，使，从而判断A，B选项正确；再据此判断函数的单调性，从而判断零点个数.

【详解】由已知得，，

，恒成立，

在上单调递增，

又

时，且存在唯一实数，使，即，

所以在上是增函数，且存在唯一极小值点，故A,B选项正确.

且在单调递减，单调递增，

又，，，所以在上有两个零点，故D选项正确，C选项错误.

故选：ABD.

【点睛】导数是研究函数的单调性、极值(最值)最有效的工具，而函数是高中数学中重要的知识点，对导数的应用的考查主要从以下几个角度进行： (1)考查导数的几何意义，往往与解析几何、微积分相联系． (2)利用导数求函数的单调区间，判断单调性；已知单调性，求参数． (3)利用导数求函数的最值(极值)，解决生活中的优化问题． (4)考查数形结合思想的应用．

13．

【分析】直接利用三角函数的周期公式求出函数的最小正周期.

【详解】由题得函数的最小正周期.

故答案为

【点睛】本题主要考查正弦型函数的最小正周期的求法，意在考查学生对该知识的理解掌握水平，属于基础题.

14．

【分析】根据求出的值，再根据向量的减法运算和向量的模即可求出答案

【详解】，，

，

则

故答案为

【点睛】本题主要考查了平面向量共线（平行）的坐标表示，解题的关键是根据向量的平行求出的值，属于基础题

15．；

【分析】基本事件总数，选出的班级中至少有一个班级来自高一年段包含的基本事件个数，由此能求出选出的班级中至少有一个班级来自高一年段的概率．

【详解】某校组织两个班级的学生参加社区劳动，这两个班级拟从高一年段的两个班级和高二年段的四个班级中选出，

 基本事件总数． 选出的班级中至少有一个班级来自高一年段包含的基本事件个数

， 则选出的班级中至少有一个班级来自高一年段的概率为．

故答案为：．

【点睛】本题考查概率的求法，考查古典概型、组合等基础知识，考查运算求解能力，是基础题．

16．10

【分析】联立直线与抛物线方程，消元、列出韦达定理，依题意，再根据焦点弦公式计算可得；

【详解】解：依题意联立直线与抛物线方程得，消去得，整理得，所以，

设，，

所以，

线段的中点的横坐标是3，所以，解得，

所以．

故答案为：．

17．(1);

(2).

【分析】（1）将正弦定理代入条件整理得，从而有，根据角的范围可得角大小；

（2）在中，由余弦定理求得，然后在中，由正弦定理求得，进一步计算可得．

【详解】（1）解：（1）因为，

由正弦定理得，

因为，所以，

所以，即，所以，

又因为，所以，所以，所以．

（2）在中，由余弦定理可得，

解得舍去，

在中，，

由正弦定理可得，

即，

解得，

所以．

18．（1）；（2）.

【解析】（1）令可求得的值，令，由可得出，两式作差可得出，且有，可知数列为等比数列，确定该数列的首项和公比，利用等比数列的通项公式可求得数列的通项公式；

（2）利用累加法可求得，，可得，进而可求得数列的前项的和.

【详解】（1）当时，，；

当时，由可得出，

两式作差得，即，则，且，

所以，数列是等比数列，且首项为，公比也为，；

（2）由题意得，，所以，且，

则，，，，，

所以，

所以，所以，

所以，易得也适合上式，

所以的前项和为.

【点睛】本题考查利用与之间的关系求通项，同时也考查了并项求和法，考查计算能力，属于中等题.

19．(1)证明见解析；

(2)在线段上存在一点，且P是靠近C的四等分点.

【分析】(1)连接，根据给定条件证明平面得即可推理作答.

(2)在平面内过C作，再以C为原点，射线CA，CB，Cz分别为x，y，z轴正半轴建立空间直角坐标系，利用空间向量计算判断作答.

【详解】（1）在三棱柱中，四边形是平行四边形，而，则是菱形，连接，如图，

则有，因，，平面，于是得平面，

而平面，则，由得，，平面，

从而得平面，又平面，

所以平面平面.

（2）在平面内过C作，由(1)知平面平面，平面平面，

则平面，以C为原点，射线CA，CB，Cz分别为x，y，z轴正半轴建立空间直角坐标系，如图，

因，，则，

假设在线段上存在符合要求的点P，设其坐标为，

则有，设平面的一个法向量，

则有，令得，而平面的一个法向量，

依题意， ，化简整理得：

而，解得，

所以在线段上存在一点，且P是靠近C的四等分点，使平面和平面所成角的余弦值为.

20．（1）4，直方图见解析；（2）分布列见解析，2.

【解析】（1）根据调查总人数可得的值，计算每组的频率除以组距，即可画出频率分布直方图；

（2）易知X所有可能取值是1，2，3，利用古典概型可得随机变量取值的概率，即可得到分布列和期望.

【详解】（1），

直方图中小矩形的高度依次为

，，，，，，

其频率分布直方图如图.

（2）因为区间岁年龄段的“投资者”有2名，区间岁年龄段“投资者”有4名，

则易知X所有可能取值是1，2，3.

则；；.

故随机变量X的分布为

故随机变量X的数学期望为.

【点睛】本题考查补全频率分布直方图、求离散型随机变量的分布列和期望，考查运算求解能力，求解时注意概率模型的确定.

21．(1)

(2)

【分析】（1）由焦点为得结合可得解；

（2）由结合韦达定理即可得解.

【详解】（1）因为为椭圆的焦点,所以又

所以所以椭圆方程为

（2）因为直线的倾斜角为,所以直线的斜率为1, 所以直线方程为,和椭圆方程联立得到,消掉,得到，

所以

所以

22．（1）0，（2），（3）证明见解析

【分析】（1）利用导数判断函数的单调区间，从而可求出函数的最大值，

（2）将问题转化为，然后通过讨论确定每段区间上函数的单调性和最值，

（3）先通过观察凑出所要证明的表达式的形式，再利用等比数列的求和公式求和，最后通过放缩法得到结论

【详解】（1）由，，得，

当时，，当时，，

所以在上递增，在上递减，

所以当时，取得最大值，即，

（2）对，总存在使得成立，等价于，

由（1）可知，即问题转化为，

当时，在上恒为正，满足题意，

当时，由，得，令，得，

所以当时，，当时，，

所以在上递减，在上递增，

当，即时，在上单调递增，则，

所以，得，所以，

当，即时，在上递减，在上递增，因为，所以只要，得，所以，

当，即时，在上单调递减，则，所以，得，不合题意，

综上，的取值范围为，

（3）由（1）得，即，

取，则，

所以，即，

所以

【点睛】关键点点睛：此题考查导数的应用，考查利用导数求函数的最值，利用导数解决不等式恒成立问题，考查放缩法证明不等式，解题的关键是由（1）的结果可得，取，则，从而可得，然后给取值，结放缩法可证得结论，考查数学转化思想，属于较难题