2023年中考数学压轴题专项训练 压轴题06二次函数与特殊四边形存在性问题（四大类型）（试题+答案）

这是一份2023年中考数学压轴题专项训练 压轴题06二次函数与特殊四边形存在性问题（四大类型）（试题+答案），文件包含2023年中考数学压轴题专项训练压轴题06二次函数与特殊四边形存在性问题四大类型答案docx、2023年中考数学压轴题专项训练压轴题06二次函数与特殊四边形存在性问题四大类型试题docx等2份试卷配套教学资源，其中试卷共75页， 欢迎下载使用。
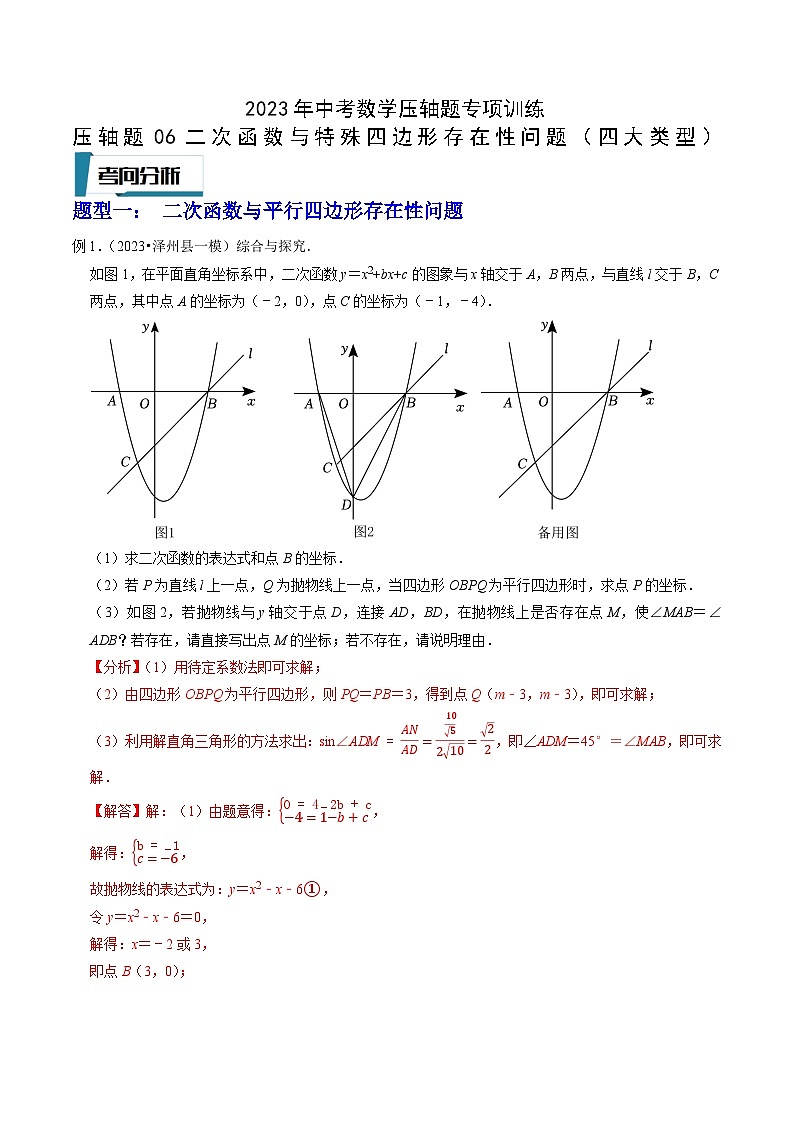
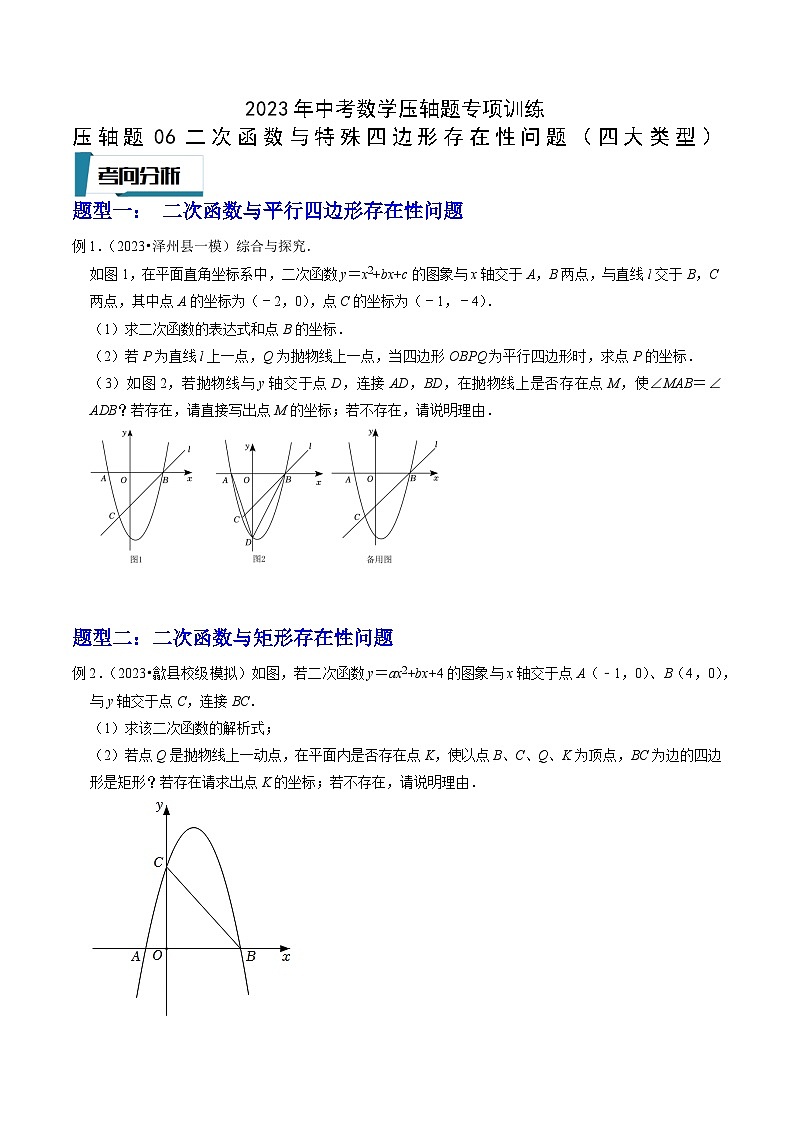
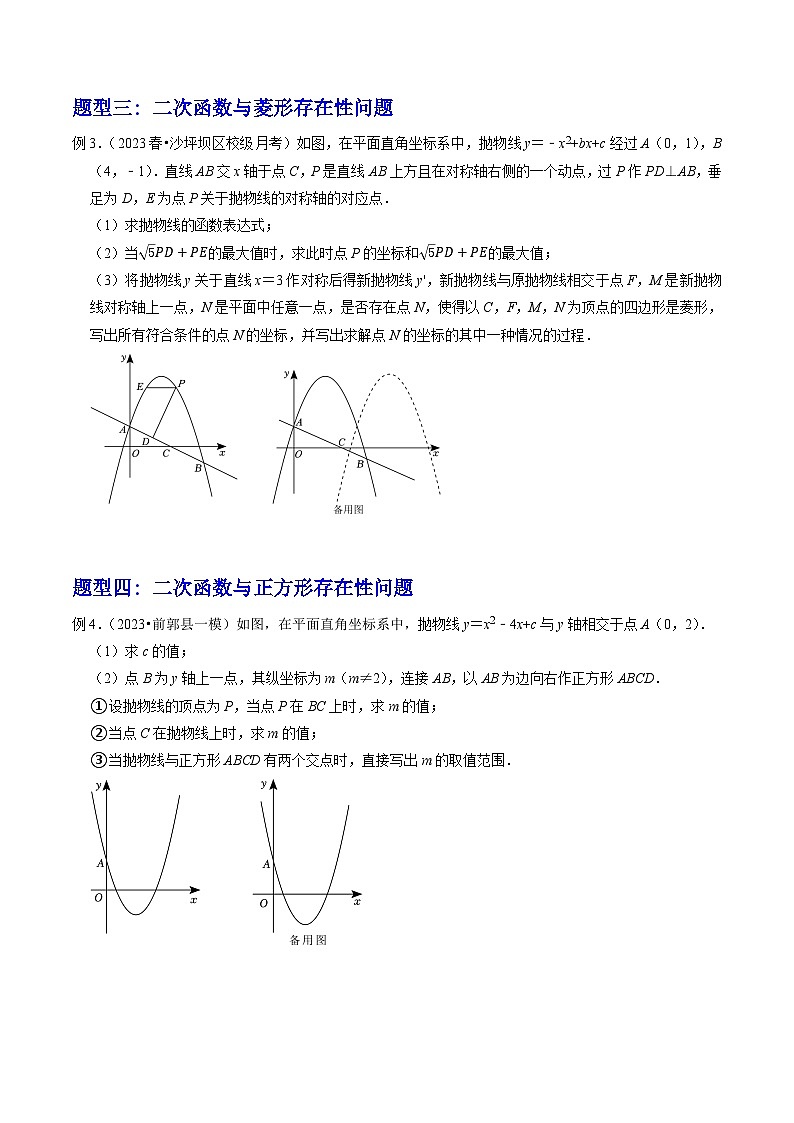
2023年中考数学压轴题专项训练压轴题06二次函数与特殊四边形存在性问题（四大类型）题型一： 二次函数与平行四边形存在性问题例1．（2023•泽州县一模）综合与探究．如图1，在平面直角坐标系中，二次函数y＝x2+bx+c的图象与x轴交于A，B两点，与直线l交于B，C两点，其中点A的坐标为（﹣2，0），点C的坐标为（﹣1，﹣4）．（1）求二次函数的表达式和点B的坐标．（2）若P为直线l上一点，Q为抛物线上一点，当四边形OBPQ为平行四边形时，求点P的坐标．（3）如图2，若抛物线与y轴交于点D，连接AD，BD，在抛物线上是否存在点M，使∠MAB＝∠ADB？若存在，请直接写出点M的坐标；若不存在，请说明理由．  题型二：二次函数与矩形存在性问题例2．（2023•歙县校级模拟）如图，若二次函数y＝ax2+bx+4的图象与x轴交于点A（﹣1，0）、B（4，0），与y轴交于点C，连接BC．（1）求该二次函数的解析式；（2）若点Q是抛物线上一动点，在平面内是否存在点K，使以点B、C、Q、K为顶点，BC为边的四边形是矩形？若存在请求出点K的坐标；若不存在，请说明理由．题型三: 二次函数与菱形存在性问题例3．（2023春•沙坪坝区校级月考）如图，在平面直角坐标系中，抛物线y＝﹣x2+bx+c经过A（0，1），B（4，﹣1）．直线AB交x轴于点C，P是直线AB上方且在对称轴右侧的一个动点，过P作PD⊥AB，垂足为D，E为点P关于抛物线的对称轴的对应点．（1）求抛物线的函数表达式；（2）当的最大值时，求此时点P的坐标和的最大值；（3）将抛物线y关于直线x＝3作对称后得新抛物线y'，新抛物线与原抛物线相交于点F，M是新抛物线对称轴上一点，N是平面中任意一点，是否存在点N，使得以C，F，M，N为顶点的四边形是菱形，写出所有符合条件的点N的坐标，并写出求解点N的坐标的其中一种情况的过程．  题型四: 二次函数与正方形存在性问题例4．（2023•前郭县一模）如图，在平面直角坐标系中，抛物线y＝x2﹣4x+c与y轴相交于点A（0，2）．（1）求c的值；（2）点B为y轴上一点，其纵坐标为m（m≠2），连接AB，以AB为边向右作正方形ABCD．①设抛物线的顶点为P，当点P在BC上时，求m的值；②当点C在抛物线上时，求m的值；③当抛物线与正方形ABCD有两个交点时，直接写出m的取值范围．  一．解答题（共20小题）1．（2023春•兴化市月考）已知：二次函数y＝ax2+2ax﹣8a（a为常数，且a＞0）的图象与x轴交于点A、B（点A在点B的左侧），与y轴交于点C，顶点为点D．（1）分别求点A、B的坐标；（2）若△ABC是直角三角形，求该二次函数相应的表达式；（3）当时，一次函数的图象过B点，与二次函数的对称轴交于Q点，N为一次函数图象上一点，过N点作y的平行线交二次函数图象于M点，当D、M、N、Q四点组成的四边形是平行四边形时，求N点的坐标．2．（2023春•沙坪坝区校级月考）如图1，在平面直角坐标系中，抛物线y＝ax2+bx+8（a≠0）与x轴交于点B（﹣4，0），点C（8，0），与y轴交于点A．点D的坐标为（0，4）．（1）求二次函数的解析式及点C的坐标．（2）如图1，点F为该抛物线在第一象限内的一动点，过E作FE∥CD，交CD于点F，求的最大值及此时点E的坐标．（3）如图2，在（2）的情况下，将原抛物线绕点D旋转180°得到新抛物线y'，点N是新抛物线y'上一点，在新抛物线上的对称轴上是否存在一点M，使得点D，E，M，N为顶点的四边形为平行四边形，若存在，请直接写出点M的坐标，并写出其中一个点M的求解过程．3．（2023•武清区校级模拟）在平面直角坐标系中，二次函数y＝ax2+bx+3的图象与x轴交于A（﹣4，0），B（2，0）两点，与y轴交于点C．（1）求这个二次函数的解析式；（2）抛物线上是否存在点Q，且满足AB平分∠CAQ，若存在，求出Q点坐标；若不存在，说明理由；（3）点N为x轴上一动点，在抛物线上是否存在点M，使以B，C，M，N为顶点的四边形是平行四边形？若存在，直接写出点M的坐标；若不存在，说明理由．   4．（2023春•承德县月考）已知二次函数与x数轴交于点A、B（A在B的左侧），与y轴交于点C，连接BC．发现：点A的坐标为 　         　，求出直线BC的解析式；拓展：如图1，点P是直线BC下方抛物线上一点，连接PB、PC，当△PBC面积最大时，求出P点的坐标；探究：如图2，抛物线顶点为D，抛物线对称轴交BC于点E，M是线段BC上一动点（M不与B、C两点重合），连接PM，设M点的横坐标为m（0＜m＜8），当m为何值时，四边形PMED为平行四边形？      5．（2023春•梅江区校级月考）如图，在平面直角坐标系中，△AOC绕原点O逆时针旋转90°得到△DOB，其中OA＝1，OC＝3．（1）若二次函数经过A、B、C三点，求该二次函数的解析式；（2）在（1）条件下，在二次函数的对称轴l上是否存在一点P，使得PA+PC最小？若P点存在，求出P点坐标；若P点不存在，请说明理由．（3）在（1）条件下，若E为x轴上一个动点，F为抛物线上的一个动点，使得B、C、E、F构成平行四边形时，求E点坐标．6．（2022秋•云州区期末）综合与探究如图，二次函数y＝ax2+bx+4的图象经过x轴上的点A（6，0）和y轴上的点B，且对称轴为直线x．（1）求二次函数的解析式．（2）点E位于抛物线第四象限内的图象上，以OE，AE为边作平行四边形OEAF，当平行四边形OEAF为菱形时，求点F的坐标与菱形OEAF的面积．（3）连接AB，在直线AB上是否存在一点P，使得△AOP与△AOB相似，若存在，请直接写出点P坐标，若不存在，请说明理由．   7．（2023春•开福区校级月考）【定义】对于函数图象上的任意一点P（x，y），我们把x+y称为该点的“雅和”，把函数图象上所有点的“雅和”的最小值称为该函数的“礼值”．根据定义回答问题：（1）①点P（9，10）的“雅和”为 　     　；（直接写出答案）②一次函数y＝3x+2（﹣1≤x≤3）的“礼值”为 　     　；（直接写出答案）（2）二次函数y＝x2﹣bx+c（bc≠0）（3≤x≤5）交x轴于点A，交y轴于点B，点A与点B的“雅和”相等，若此二次函数的“礼值”为1﹣b，求b，c的值；（3）如图所示，二次函数y＝x2﹣px+q的图象顶点在“雅和”为0的一次函数的图象上，四边形OABC是矩形，点B的坐标为（5，﹣3），点O为坐标原点，点C在x轴上，当二次函数y＝x2﹣px+q的图象与矩形的边有四个交点时，求p的取值范围．  8．（2023春•无锡月考）在平面直角坐标系中，O为坐标原点，二次函数y＝ax2﹣2ax﹣3a（a＞0）的图象分别与x轴交于A、B两点（点A在点B左侧），与y轴交于点C，过点B作BC的垂线交对称轴于点M，以BM、BC为邻边作矩形BMNC．（1）求A、B的坐标；（2）当点N恰好落在函数图象上时，求二次函数的表达式；（3）作点N关于MC的对称点N'，则点N'能否落在函数图象的对称轴上，若能，请求出二次函数的表达式；若不能，请说明理由．     9．（2022秋•开福区校级期末）若凸四边形的两条对角线所夹锐角为60°，我们称这样的凸四边形为“美丽四边形”． （1）①在“平行四边形、矩形、菱形、正方形”中，一定不是“美丽四边形”的有 　         　；②若矩形ABCD是“美丽四边形”，且AB＝1，则BC＝　                  　；（2）如图1，“美丽四边形”ABCD内接于⊙O，AC与BD相交于点P，且对角线AC，为直径，AP＝2，PC＝8，求另一条对角线BD的长；（3）如图2，平面直角坐标系中，已知“美丽四边形”ABCD的四个顶点A（﹣2，0），C（1，0），B在第三象限，D在第一象限，AC与BD交于点O，且四边形ABCD的面积为6，若二次函数y＝ax2+bx+c（a、b、c为常数，且a≠0）的图象同时经过这四个顶点，求a的值．  10．（2022秋•南关区校级期末）在平面直角坐标系中，二次函数y＝x2﹣2x+n（x＞0）的图象记为G1，将G1绕坐标原点旋转180°得到图象G2，图象G1和G2合起来记为图象G．（1）若点P（﹣2，3）在图象G上，求n的值．（2）当n＝﹣1时．①若O（t，1）在图象G上，求t的值．②当k≤x≤3（k＜3）时，图象G对应函数的最大值为2，最小值为﹣2，直接写出k的取值范围．（3）当以A（﹣2，2），B（﹣2，﹣1），C（1，﹣1），D（1，2）为顶点的矩形ABCD的边与图象G有且只有3个公共点时，直接写出n的取值范围．      11．（2022•株洲）已知二次函数y＝ax2+bx+c（a＞0）．（1）若a＝1，b＝3，且该二次函数的图象过点（1，1），求c的值；（2）如图所示，在平面直角坐标系xOy中，该二次函数的图象与x轴相交于不同的两点A（x1，0）、B（x2，0），其中x1＜0＜x2、|x1|＞|x2|，且该二次函数的图象的顶点在矩形ABFE的边EF上，其对称轴与x轴、BE分别交于点M、N，BE与y轴相交于点P，且满足tan∠ABE．①求关于x的一元二次方程ax2+bx+c＝0的根的判别式的值；②若NP＝2BP，令Tc，求T的最小值．阅读材料：十六世纪的法国数学家弗朗索瓦•韦达发现了一元二次方程的根与系数之间的关系，可表述为“当判别式Δ≥0时，关于x的一元二次方程ax2+bx+c＝0（a≠0）的两个根x1、x2有如下关系：x1+x2，x1x2”．此关系通常被称为“韦达定理”．12．（2023春•南关区月考）已知抛物线ybx+c（b、c是常数）的顶点B坐标为（﹣1，2），抛物线的对称轴为直线l，点A为抛物线与x轴的右交点，作直线AB．点P是抛物线上的任意一点，其横坐标为m，过点P作x轴的垂线交直线AB于点Q，过点P作PN⊥l于点N，以PQ、PN为边作矩形PQMN．（1）b＝　     　，c＝　                　．（2）当点Q在线段AB上（点Q不与A、B重合）时，求PQ的长度d与m的函数关系式，并直接写出d的最大值．（3）当抛物线被矩形PQMN截得的部分图象的最高点纵坐标与最低点纵坐标的距离为2时，求点P的坐标． 13．（2023春•南关区校级月考）在平面直角坐标系中，抛物线y＝﹣x2+bx+c（b、c是常数）经过点A（﹣1，0）和点B（3，0）．点P在抛物线上，且点P的横坐标为m．（1）求b、c的值；（2）当△PAB的面积为8时，求m的值；（3）当点P在点A的右侧时，抛物线在点P与点A之间的部分（包含端点）记为图象G，设G的最高点与最低点的纵坐标之差为h，求h与m之间的函数关系式；（4）点Q的横坐标为1﹣3m，纵坐标为m+1，以PQ为对角线构造矩形，且矩形的边与坐标轴平行．当抛物线在矩形内部的点的纵坐标y随x的增大而增大或y随x的增大而减小时，直接写出m的取值范围．          14．（2023•九台区校级一模）在平面直角坐标系中，已知抛物线y＝x2﹣2ax﹣a（a为常数）．（1）若点（2，﹣1）在抛物线上．①求抛物线的表达式；②当x为何值时y随x的增大而减小？（2）若x≤2a，当抛物线的最低点到x轴的距离恰好是1时，求a的值；（3）已知A（﹣1，1）、，连结AB．当抛物线与线段AB有交点时，该交点为P（点P不与A、B重合），将线段PB绕点P顺时针旋转90°得到线段PM，以PM、PA为邻边构造矩形PMQA．当抛物线在矩形PMQA内部（包含边界）图象所对应的函数的最大值与最小值的差为时，直接写出a的值．        15．（2023•靖江市校级模拟）如图，在平面直角坐标系中，抛物线yx2+bx与x轴正半轴交于点A，且点A的坐标为（3，0），过点A作垂直于x轴的直线l．P是该抛物线上的任意一点，其横坐标为m，过点P作PQ⊥l于点Q，M是直线l上的一点，其纵坐标为﹣m，以PQ、QM为边作矩形PQMN． （1）求b的值．（2）当点Q与点M重合时，求m的值．（3）当矩形PQMN是正方形，且抛物线的顶点在该正方形内部时，求m的值．（4）当抛物线在矩形PQMN内的部分所对应的函数值y随x的增大而减小时．直接写出m的取值范围．  16．（2022秋•临朐县期末）如图，在平面直角坐标系中，O是坐标原点，菱形OABC的顶点A（3，4），C在x轴的负半轴，抛物线y＝ax2+bx+c的对称轴x＝2，且过点O，A．（1）求抛物线y＝ax2+bx+c的解析式；（2）若在线段OA上方的抛物线上有一点P，求△PAO面积的最大值，并求出此时P点的坐标；（3）若把抛物线y＝ax2+bx+c沿x轴向左平移m个单位长度，使得平移后的抛物线经过菱形OABC的顶点B．直接写出平移后的抛物线解析式．   17．（2023•道外区一模）如图，在平面直角坐标系中，点O为坐标原点，抛物线y＝ax2﹣2ax+c经过点A（﹣4，0），点C（0，6），与x轴交于另一点B．（1）求抛物线的解析式；（2）点D为第一象限抛物线上一点，连接AD，BD，设点D的横坐标为t，△ABD的面积为S，求S关于t的函数解析式（不要求写出自变量t的取值范围）；（3）在（2）的条件下，点P为第四象限抛物线上一点，连接PA交y轴于点E，点F在线段BC上，点G在直线AD上，若，四边形BEFG为菱形，求点P的坐标．  18．（2023春•九龙坡区校级月考）如图，在平面直角坐标系中，抛物线y与x轴交于A（﹣1，0），B（4，0），与y轴于点C，连接BC，D为抛物线的顶点．（1）求该抛物线的解析式；（2）点P为直线BC下方抛物线上的一动点，过P作PE⊥BC于点E，过P作PF⊥x轴于点F，交直线BC于点G，求PE+PG的最大值，以及此时点P的坐标；（3）将抛物线y沿射线CB方向平移，平移后的图象经过点H（2，﹣1），点M为D的对应点，平移后的抛物线与y轴交于点N，点Q为平移后的抛物线对称轴上的一点，且点Q在第一象限．在平面直角坐标系中确定点R，使得以点M，N，Q，R为顶点的四边形为菱形，请写出所有符合条件的点R的坐标，并写出求解点R的坐标的其中一种情况的过程．19．（2023•安徽一模）如图，在平面直角坐标系中，抛物线C1：的图象与坐标轴交于A、B、C三点，其中点A的坐标为（0，8），点B的坐标为（﹣4，0），点D的坐标为（0，4）．（1）求该二次函数的表达式及点C的坐标；（2）若点F为该抛物线在第一象限内的一动点，求△FCD面积的最大值；（3）如图2，将抛物线C1向右平移2个单位，向下平移5个单位得到抛物线C2，M为抛物线C2上一动点，N为平面内一动点，问是否存在这样的点M、N，使得四边形DMCN为菱形，若存在，请直接写出点N的坐标；若不存在，请说明理由．   20．（2023•九台区一模）在平面直角坐标系中，抛物线y＝x2+bx+c（b、c是常数）经过点（﹣2，﹣1），点（1，2）．点A在抛物线上，且点A的横坐标为m（m≠0）．以点A为中心，构造正方形POMN，PQ＝2|m|，且PQ⊥x轴．（1）求该抛物线对应的函数表达式；（2）若点B是抛物线上一点，且在抛物线对称轴右侧．过点B作x轴的平行线交抛物线于另一点C，连接BC．当BC＝6时，求点B的坐标；（3）若m＜0，当抛物线在正方形内部的点的纵坐标y随x的增大而增大或y随x的增大而减小时，求m的取值范围；（4）当抛物线与正方形PQMN的边只有2个交点，且交点的纵坐标之差为时，直接写出m的值．