湖南省长郡、雅礼、一中2021届高三上学期联合考试理科数学试题 Word版含答案

这是一份湖南省长郡、雅礼、一中2021届高三上学期联合考试理科数学试题 Word版含答案，共19页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
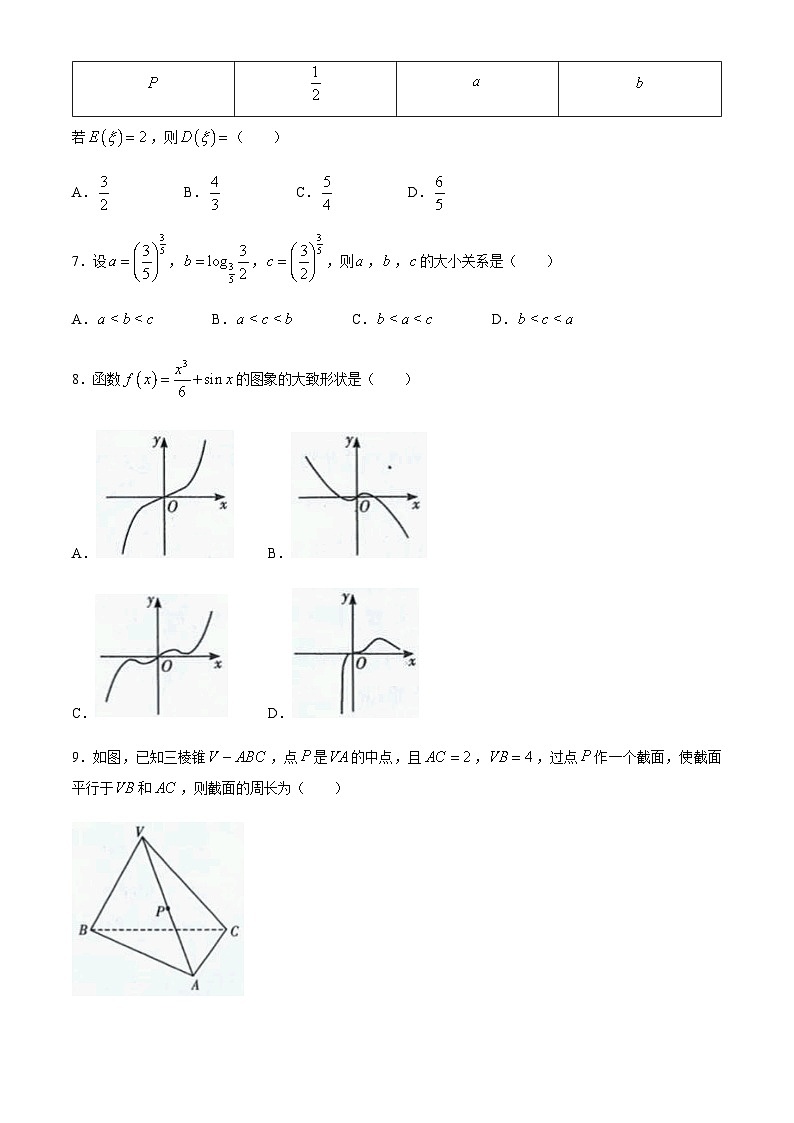
湖南省长郡、雅礼、一中2021届高三月考试卷一（全国卷）数学（理科）一、选择题1．已知集合，，则（    ）A．    B．C．   D．2．若复数满足，则下列说法正确的是（    ）A．的虚部为  B．为实数  C．  D．3．\展开式中项的系数为（    ）A．   B．   C．15   D．54．设，若单位向量，满足：且向量与的夹角为，则（    ）A．   B．   C．   D．15．已知数列满足，则（    ）A．  B．  C．  D．6．随机变量的分布列如表：124若，则（    ）A．   B．   C．   D．7．设，，，则，，的大小关系是（    ）A．  B．  C．  D．8．函数的图象的大致形状是（    ）A．  B．C．  D．9．如图，已知三棱锥，点是的中点，且，，过点作一个截面，使截面平行于和，则截面的周长为（    ）A．12   B．10   C．8   D．610．技术的数学原理之一便是著名的香农公式：．它表示：在受噪声干挠的信道中，最大信息传递速率取决于信道带宽、信道内信号的平均功率、信道内部的高斯噪声功率的大小，其中叫做信噪比．按照香农公式，若不改变带宽，而将信噪比从1000提升至2000，则大约增加了（参考数据：）（    ）A．  B．  C．  D．11．已知函数在区间恰有3个零点，则的取值范围是（    ）A．  B．  C．  D．12．已知双曲线（，），过原点任作一条直线，分别交双曲线两支于点，（点在第一象限），点为的左焦点，且满足，，则的离心率为（    ）A．   B．   C．   D．2二、填空题13．甲、乙、丙、丁4名学生参加体育锻炼，每人在，，三个锻炼项目中恰好选择一项进行锻炼，则甲不选项、乙不选B项的概率为______．14．已知锐角、满足，则的最小值为______．15．如图，已知圆锥底面圆的直径与侧棱、构成边长为的正三角形，点是底面圆上异于，的动点，则、、、四点所在球面的半径是______．16．已知点，，动点，分别在直线和上，且与两直线垂直，则的最小值为______．三、解答题（一）必考题17．圆的内接四边形中，，，．（1）求的长度；（2）求圆的半径．18．三棱柱中，平面，且，，，为中点．（1）求四面体的体积；（2）求平面与所成锐二面角的余弦．19．已知椭圆的离心率为，且经过点．（1）求椭圆的方程．（2）设为椭圆上非顶点的任意一点，若、分别为椭圆的左顶点和上顶点，直线交轴于，直线交轴于，，问：的值是不是定值？若为定值，求之，若不为定值，说明理由．20．如图，一只蚂蚁从单位正方体的顶点出发，每一步（均为等可能性的）经过一条边到达另一顶点，设该蚂蚁经过步回到点的概率为．（1）分别写出，的值；（2）设一只蚂蚁从顶点出发经过步到达点的概率为，求的值；（3）求．21．（1）求的最大值；（2）若对恒成立，求实数的取值范围．（二）选考题22．选修4-4：坐标系与参数方程已知在直角坐标系中，曲线的参数方程为（为参数），在极坐标系（以坐标原点为极点，轴的正半轴为极轴）中，曲线的方程为，曲线，交于，两点，其中定点．（1）若，求的值；（2）若，，成等比数列，求的值．23．选修4-5：不等式选讲已知函数，．（1）若不等式无解，求实数的取值范围；（2）当时，函数的最小值为2，求实数的值．2021届高三月考试卷一（全国卷）数学（理科）参考答案1．【答案】B【解析】【解答】解：∵，．故选B．2．【答案】C【解析】【解答】解：因为，所以．故选C．3．【答案】B【解析】【解答】解：展开式中项的系数：；展开式中项的系数：；故展开式中项的系数为．故选B．4．【答案】A【解析】【解答】解：根据题意，设，，∴，，∴，解得．故选A．5．【答案】D【解析】【解答】解：由题意，可知，则，∴．故选D6．【答案】A【解析】【解答】解：，解得；．故选A．7．【答案】C【解析】【解答】解：∵，，，∴．故选C．8．【答案】A【解析】【解答】解：因为，所以函数为奇函数，排除选项D；，当时，，，所以，单调递增；当时，，，所以，也是单调递增．综上可知，在上单调递增，排除选项B和C．故选A．9．【答案】D【解析】【解答】如图所示，过点作，交于点，过点作交于点，过点作，交于点；由作图可知：，所以四边形是平行四边形；可得，；所以截面四边形的周长为．故选D．10．【答案】A【解析】【解答】解：将信噪比从1000提升至2000时，，故大约增加了．故选A．11．【答案】D【解析】【解答】解：问题等价于函数在区间恰有3个零点，故，于是可得．故选D．12．【答案】A【解析】【解答】解：由题意可知：双曲线的右焦点，由关于原点的对称点为，则|，∴四边形为平行四边形，则，，由，根据双曲线的定义，∴，，．∴，在中，，，，∴，整理得：，则双曲线的离心率．故选A．13．【答案】【解析】【解答】解：法一：每位学生选择三个锻炼项目有种，则4人总的选择方式共有种，其中甲、乙的选择方式有种，其余两人仍有种，故甲不选、乙不选项目的概率为．法二：只考虑甲、乙的选择，不加限制均为3种，受到限制后均为2种，而甲乙的选择相互独立，故甲不选、乙不选项目的概率为．故答案为．14．【答案】18【解析】【解答】解：∵，∴，设，，则，∵，均为锐角，∴，，∴，当且仅当，即，即，时，等号成立．∴的最小值为18．故答案为18．15．【答案】2【解析】【解答】解：如图，设底面圆的圆心为，、、、四点所在球面的球心为，连接，则平面，且在线段上．易知，．设球的半径为，在中，由勾股定理得，解得．故答案为2．16．【答案】【解析】【解答】解：设，由于与两直线垂直且，则，故．此式可理解为点到及的距离之和，其最小值即为．故所求最小值为．故答案为．17．【答案】（1）设圆半径为，由正弦定理，，，∴，又．故．而．∴．设，则．∴．∴．即．（2），∴，∴．∴．【解析】18．【答案】解：（1）．（2）设为中点，为中点，以射线，，为非负，，轴．建立空间直角坐标系，则，，，，．∴，，，．设平面，则取，设平面，则取，．故平面与平面所成锐二面角的余弦为．【解析】19．【答案】解：（1），设椭圆方程为，将点坐标代入可得，故椭圆方程为即．（2）设，，由、、共线可知，由、、共线可知．，．∴，由于，∴．【解析】20．【答案】解：（1），．（2）由于从顶点出发经过步到达点的概率为，则由出发经过步到达点，的概率也是，为奇数时，所以，为偶数时，由出发经过步不可能到，，，这四个点，．（3）同理，由，，分别经2步到点的概率都是，由出发经过（为偶数）步再回到的路径分为以下四类：①由经历步到，再经2步回到，概率为；②由经历步到，再经2步回到．概率为；③由经历步到，再经2步回到．概率为；④由经历步到，再经2步回到．概率为；所以，结合．消元得：，即，所以，故．综上所述，．【解析】21．【答案】解：（1），则，令得．故在单调递增，在单调递减，∴．（2）设，由得，则．①若，则时，，，，，此时对恒成立，故在单调递减，，故符合要求．②若，由于故，∴，而对恒成立，∴．∴符合要求，综上，的取值范围为．【解析】22．【答案】（1）∵曲线的方程为，∴，即．∴曲线的直角坐标方程为，又已知，∴曲线的直角坐标方程为．将曲线的参数方程（为参数），与联立，得，由于，∴设方程两根为，，则，，∴．（2）将曲线的参数方程（为参数），与联立，得，由于，∴设方程两根为，，则，，且，，又，，成等比数列，∴，得，则，即．∴，得，解得，又，∴，∴当，，成等比数列时，得值为．【解析】23．【答案】解：（1）∵，∴由，得，∵不等式无解．∴，又∵，∴，∴或，∴实数的取值范围是．（2）∵，∴，∴，由图可知当时，，∴符合题意，∴．